Question: The average energy E (in kcal) needed
The average energy E (in kcal) needed for a lizard to walk or run a distance of 1 km has been modeled by the equation
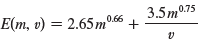
where m is the body mass of the lizard (in grams) and v is its speed (in km/h). Calculate Em (400, 8) and Ev (400, 8) and interpret your answers.
Transcribed Image Text:
E(m, v) = o6 + 3.5m0.75 2.65 m 0.66
> Unexplained changes are common in financial statements.
> Data-driven fraud detection can pay large dividends and is an effective way to reduce the cost of fraud in any organization.
> Digital analysis using Benford's Law can be performed on databases of any size.
> Understanding the kinds of frauds that can occur is not important when using a data-driven detection method.
> When using Benford's Law, potential suspects are less likely to know you are trying to detect fraud than if you use more direct detection techniques.
> According to Benford's Law, the first digit of natural sets of numbers will begin with a 9 more often than with an 8.
> Data-driven analysis uses the company's database to search for normal relationships between numbers.
> ODBC is the best approach to import because it achieves a direct, rich connection to the source database.
> Studies have found that the most common internal control problem when frauds occur is having a lack of proper authorizations.
> Before financial institutions can sell or disclose confidential customer information, they must provide customers with the opportunity to "opt out" from information sharing.
> Most people who commit fraud feel a perceived financial pressure.
> Because of the nature of fraud, auditors are often in the best position to detect its occurrence.
> Fraud is a crime that is seldom observed.
> A single symptom (red flag) is almost always enough information to identify the type of fraud scheme occurring.
> The z-score calculation is the best way to stratify data.
> Vertical analysis is a useful detection technique because percentages are easily understood.
> Vertical analysis is a more direct method than horizontal analysis in focusing on changes in financial statements from one period to another.
> Balance sheets must be converted to change statements before they can be used in detecting fraud.
> Unusual patterns always indicate the existence of fraud.
> First-time offenders usually exhibit no psychological changes.
> The Gramm-Leach-Bliley Act of 1999 made it more difficult for officials and private citizens to access information from financial institutions.
> As fraud perpetrators become more confident in their fraud schemes, they usually steal and spend increasingly larger amounts.
> Most people who commit fraud use the embezzled funds to save for retirement.
> Analytical fraud symptoms are the least effective way to detect fraud.
> The internal control system of an organization is comprised of the control environment, the accounting system, and control procedures (activities).
> Internal control weaknesses give employees opportunities to commit fraud.
> A check is an example of a source document.
> Recording an expense is a possible way to conceal the theft of cash.
> Some complaints and tips turn out to be unjustified.
> Auditors can best help detect fraud at the conversion stage.
> The three elements of a typical fraud consist of concealment, conversion, and completion.
> Conversion is the third element of the fraud investigation triangle.
> It is safe to assume that fraud has not occurred if one or more elements of the fraud triangle cannot be observed.
> Psychopaths feel no guilt because they have no conscience.
> Analytical anomalies are present in every fraud.
> The increasingly complex nature of business helps to decrease the number of collusive frauds.
> Even a good system of internal controls will often not be completely effective because of fallibilities of the people applying and enforcing the controls.
> Not prosecuting fraud perpetrators is cost-effective both in the short run and the long run.
> The two elements in creating a positive work environment are (1) having an open-door policy and (2) having positive personnel and operating procedures.
> When fraud is committed, the problem is often not a lack of controls, but the overriding of existing controls by management and others.
> A good internal control system within a company can ensure the absence of fraud.
> An important factor in creating a culture of honesty, openness, and assistance in the workplace is maintaining an employee assistance program.
> For various reasons, the net worth method tends to be a conservative estimate of amounts stolen.
> Perpetrators usually save what they steal.
> The ellipsoid 4x2 + 2y2 + z2 = 16 intersects the plane y = 2 in an ellipse. Find parametric equations for the tangent line to this ellipse at the point (1, 2, 2).
> The paraboloid z = 6 - x - x2 - 2y2 intersects the plane x = 1 in a parabola. Find parametric equations for the tangent line to this parabola at the point (1, 2, -4). Use a computer to graph the paraboloid, the parabola, and the tangent line on the same
> You are told that there is a function f whose partial derivatives are fx (x, y) = x + 4y and fy (x, y) = 3x - y. Should you believe it?
> A contour map is given for a function f. Use it to estimate fx (2, 1) and fy (2, 1). -3 6. -2 10 12 14. 2 16 3 18
> The following surfaces, labeled a, b, and c, are graphs of a function f and its partial derivatives fx and fy. Identify each surface and give reasons for your choices. 8 4 -4 a -8 -2 -3 -2 -1 0 1 2 y 2. 3. 4 -4 -3 -2 -1 0 1 3 y -4 -8- -2 -3 -2 -1 0
> A model for the surface area of a human body is given by the function S = f (w, h) = 0.1091w0.425h0.725 where w is the weight (in pounds), h is the height (in inches), and S is measured in square feet. Calculate and interpret the partial derivatives.
> Find the limit, if it exists, or show that the limit does not exist. ху lim (x y-0, 0) Vx2 + y?
> Let g (x, y) = cos (x + 2y). (a). Evaluate g (2, -1). (b). Find the domain of g. (c). Find the range of g.
> Find the limit, if it exists, or show that the limit does not exist. 5y cos?x lim (x, y)(0, 0) x + y* 4
> Find the limit, if it exists, or show that the limit does not exist. x* – 4y? lim (x, y (0, 0) x? + 2y?
> Find the limit, if it exists, or show that the limit does not exist. lim (x, y)- (3, 2) evzi-y
> Find the limit, if it exists, or show that the limit does not exist. lim (x, y)- (m, w/2) y sin(x – y)
> Use a table of numerical values of f (x, y) for (x, y) near the origin to make a conjecture about the value of the limit of f (x, y) as (x, y) → (0, 0). Then explain why your guess is correct. 2ху f(x, y) = x² + 2y²
> Use a table of numerical values of f (x, y) for (x, y) near the origin to make a conjecture about the value of the limit of f (x, y) as (x, y) → (0, 0). Then explain why your guess is correct. x*y* + x*y* ² – 5 2 f(x, y) = 2 - xy
> Explain why each function is continuous or discontinuous. (a). The outdoor temperature as a function of longitude, latitude, and time (b). Elevation (height above sea level) as a function of longitude, latitude, and time (c). The cost of a taxi ride as a
> Suppose that lim (x, y) → (3, 1) f (x, y) = 6. What can you say about the value of f (3, 1)? What if f is continuous?
> Graph the functions In general, if t is a function of one variable, how is the graph of obtained from the graph of t? f(x, y) = /x² + y² f(x, y) = evya f(x, y) = Inx? + y2 f(x, y) = sin(/r? + y² 1 f(x, y) x² + y? f(x, y) = 9(Vx² + y?)
> Find the velocity, acceleration, and speed of a particle with the given position function. Sketch the path of the particle and draw the velocity and acceleration vectors for the specified value of t. r(t) = t i + 2 cos t j + sin t k, t = 0
> Use a computer to investigate the family of surfaces z = x2 + y2 + cxy. In particular, you should determine the transitional values of c for which the surface changes from one type of quadric surface to another.
> Use a computer to investigate the family of surfaces z = (ax2 + by2) e-x2-y2 How does the shape of the graph depend on the numbers a and b?
> Investigate the family of functions f (x, y) = ecx2+y2. How does the shape of the graph depend on c?
> Graph the function using various domains and viewpoints. Comment on the limiting behavior of the function. What happens as both x and y become large? What happens as (x, y) approaches the origin? f(x, y) x? + y?
> Graph the function using various domains and viewpoints. Comment on the limiting behavior of the function. What happens as both x and y become large? What happens as (x, y) approaches the origin? x + y f(x, y) = x? + y?
> Use a computer to graph the function using various domains and viewpoints. Get a printout that gives a good view of the “peaks and valleys.” Would you say the function has a maximum value? Can you identify any points on the graph that you might consider
> Use a computer to graph the function using various domains and viewpoints. Get a printout that gives a good view of the “peaks and valleys.” Would you say the function has a maximum value? Can you identify any points on the graph that you might consider
> Describe how the graph of g is obtained from the graph of f. (a). t (x, y) = f (x - 2, y) (b). t (x, y) = f (x, y + 2) (c). t (x, y) = f (x + 3, y – 4)
> Describe how the graph of g is obtained from the graph of f . (a). t (x, y) = f (x, y) + 2 (b). t (x, y) = 2f (x, y) (c). t (x, y) = -f (x, y) (d). t (x, y) = 2 - f (x, y)
> Describe the level surfaces of the function. f (x, y, z) = x2 - y2 - z2
> Find the velocity, acceleration, and speed of a particle with the given position function. Sketch the path of the particle and draw the velocity and acceleration vectors for the specified value of t. r(t) = t i + t2 j + 2 k, t = 1
> If c ∈ Vn, show that the function f given by f (x) = c ∙ x is continuous on Rn.
> Show that the function f given by f (x) = |x | is continuous on Rn. [Hint: Consider |x - a |2 = (x – a) ∙ (x – a).]
> Let (a). Show that f (x, y) → 0 as (x, y) → (0, 0) along any path through s0, 0d of the form y = mxu with 0 (b). Despite part (a), show that f is discontinuous at (0, 0). (c). Show that f is discontinuous on two enti
> Graph and discuss the continuity of the function sin xy if ху # 0 f(x, y) = ху 1 if xy = 0
> Match the function (a) with its graph (labeled A–F below) and (b) with its contour map (labeled I–VI). Give reasons for your choices. z = (1 - x2) (1 - y2) B D E II III IV VI yA (OKO C O O O O).O O O) O O KO C O
> Match the function (a) with its graph (labeled A–F below) and (b) with its contour map (labeled I–VI). Give reasons for your choices. z = sin x - sin y B D E II III IV VI yA (OKO C O O O O).O O O) O O KO C O OD
> Determine the set of points at which the function is continuous. ху if (x, y) # (0, 0) 2 f(x, y) = if (x, y) = (0, 0)
> Determine the set of points at which the function is continuous. x²y³ f(x, y) = { ² 2.x² + if (x, y) + (0, 0) 1 if (x, y) = (0, 0)
> Match the function (a) with its graph (labeled A–F below) and (b) with its contour map (labeled I–VI). Give reasons for your choices. z = sin(xy) B D E II III IV VI yA (OKO C O O O O).O O O) O O KO C O OD O
> Determine the set of points at which the function is continuous. f (x, y, z) = arcsin (x2 + y2 + z2)
> Find the velocity, acceleration, and speed of a particle with the given position function. Sketch the path of the particle and draw the velocity and acceleration vectors for the specified value of t. r(t) = et i + e2t j, t = 0
> Determine the set of points at which the function is continuous. G (x, y) = ln (1 + x – y)
> Determine the set of points at which the function is continuous. e* + e H(x, y) = eу — 1
> Use a computer to graph the function using various domains and viewpoints. Get a printout of one that, in your opinion, gives a good view. If your software also produces level curves, then plot some contour lines of the same function and compare with the
> Graph the function and observe where it is discontinuous. Then use the formula to explain what you have observed. 1 f(x, y) = 1 – x² – y? ,2
> Graph the function and observe where it is discontinuous. Then use the formula to explain what you have observed. f (x, y) = e1/(x-y)
> Sketch both a contour map and a graph of the function and compare them. f(x, y) = V36 – 9x² – 4y²
> Sketch both a contour map and a graph of the function and compare them. f (x, y) = x2 + 9y2
> Find h (x, y) = g (f (x, y)) and the set of points at which h is continuous. g(t) = t + In t, f(x, y) : 1 - ху 1+ x?y? .2,2
> Use a computer graph of the function to explain why the limit does not exist. хуз lim (x, y)(0, 0) x? + y6
> Find the limit, if it exists, or show that the limit does not exist. xy4 lim (x, y)- (0, 0) x + y® ,2 8
> The temperature-humidity index I (or humidex, for short) is the perceived air temperature when the actual temperature is T and the relative humidity is h, so we can write I = f (T, h). The following table of values of I is an excerpt from a table compile
> The wave heights h in the open sea depend on the speed v of the wind and the length of time t that the wind has been blowing at that speed. Values of the function h = f (v, t) are recorded in feet in Table 4. Table 4: (a). What is the value of f (40,
> Two contour maps are shown. One is for a function f whose graph is a cone. The other is for a function t whose graph is a paraboloid. Which is which, and why?
> Level curves (isothermals) are shown for the typical water temperature (in 0C) in Long Lake (Minnesota) as a function of depth and time of year. Estimate the temperature in the lake on June 9 (day 160) at a depth of 10 m and on June 29 (day 180) at a dep
> Shown is a contour map of atmospheric pressure in North America on August 12, 2008. On the level curves (called isobars) the pressure is indicated in millibars (mb). (a). Estimate the pressure at C (Chicago), N (Nashville), S (San Francisco), and V (Va
> The position function of a spaceship is and the coordinates of a space station are (6, 4, 9). The captain wants the spaceship to coast into the space station. When should the engines be turned off? 4 r(t) = (3 + f)i + (2 + In f) j + (7- k t2 + 1,

