Question: The cross section of an unbalanced wide
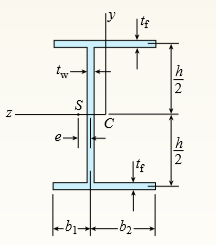
The cross section of an unbalanced wide flange beam is shown in the figure. Derive the following formula for the distance e from the centerline of the web to the shear center S:
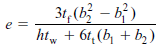
Also, check the formula for the special cases of a channel section (b1 = 0 and b2 = b) and a doubly symmetric beam (b1 = b2 = b/2).
Transcribed Image Text:
3t,(b; – b} ) e = ht, + 61, (b + by)
> Solve Problem 10 by using Mohr’s circle for plane strain. Data from Problem 10: Solve the preceding problem for the following data: εx = 190 × 1026, εy = -230 × 1026, γxy
> Solve Problem 9 by using Mohr’s circle for plane strain. Data from Problem 9: An element of material subjected to plane strain (see figure) has strains of εx = 280 × 1026, εy = 420 ×
> The strains on the surface of an experimental device made of pure aluminum (E = 70 GPa, v = 0.33) and tested in a space shuttle were measured by means of strain gages. The gages were oriented as shown in the figure, and the measured strains were Î&
> On the surface of a structural component in a space vehicle, the strains are monitored by means of three strain gages arranged as shown in the figure. During a certain maneuver, the following strains were recorded: εa = 1100 × 1
> A 60° strain rosette, or delta rosette, consists of three electrical-resistance strain gages arranged as shown in the figure. Gage A measures the normal strain εa in the direction of the x axis. Gages B and C measure the strains &
> A solid circular bar with a diameter of d = 1.25 in is subjected to an axial force P and a torque T (see figure). Strain gages A and B mounted on the surface of the bar give readings εA = 140 × 1026 and εB = 260 &At
> A 45° strain rosette (see figure) mounted on the surface of an automobile frame gives the following readings: gage A = 310 × 1026; gage B = 180 × 1026; and gage C = -160 × 1026. Determine the principal st
> During a test of an airplane wing, the strain gage readings from a 45° rosette (see figure) are as follows: gage A = 520 × 1026 ; gage B = 360 × 1026; and gage C = -80 × 1026. Determine the principal stra
> A hollow steel box beam has the rectangular cross section shown in the figure. Determine the maximum allowable shear force V that may act on the beam if the allowable shear stress is 36 MPa. 20 mm 10 mm 10 mm 450 20 Įmm 200 mm
> Solve the preceding problem for the following data: σx = -150 MPa, σy = -210 MPa, τxy = -16 MPa, and θ = 50°. The material is brass with E = 100 GPa and v = 0.34. Data from Problem 17: An elemen
> An element in plane stress is subjected to stresses σx = -8400 psi, σy = 1100 psi, and τxy = -1700 psi (see figure). The material is aluminum with modulus of elasticity E = 10,000 ksi and Poisson’s ratio
> Solve the preceding problem if the plate is made of aluminum with E = 72 GPa and Poisson’s ratio v = 0.33. The plate is loaded in biaxial stress with normal stress σx = 79 MPa, angle ∅ = 18°, and
> A brass plate with a modulus of elasticity E = 16 × 106 psi and Poisson’s ratio v = 0.34 is loaded in biaxial stress by normal stresses σx and σy (see figure). A strain gage is bonded to the plate at a
> Solve the preceding problem for the following data: εx = 21120 × 1026, εy = 2430 × 1026 , γxy = 780 × 1026, and θ = 45°. Data from Problem 13: An elem
> An element of material in plane strain (see figure) is subjected to strains εx = 480 × 1026, εy = 70 × 1026, and γxy = 420 × 1026. Determine the following quantities: (a) the st
> Solve the preceding problem for the following strains: εx = 120 × 1026, εy = -450 × 1026, and γxy = -360 × 1026. Data from Problem 11: The strains for an element of material
> The strains for an element of material in plane strain (see figure) are as follows: εx = 480 × 1026, εy = 140 × 1026, and γxy = -350 × 1026. Determine the principal strains and
> Solve the preceding problem for the following data: εx = 190 × 1026, εy = 230 × 1026, γxy = 160 × 1026, and θ = 40°. Data from Problem 9: An element o
> An element of material subjected to plane strain (see figure) has strains of εx = 280 × 1026, εy = 420 × 1026, and γxy = 150 × 1026. Calculate the strains for an element oriente
> A simple beam with an overhang supports a uniform load of intensity q = 1200 lb/ft and a concentrated P = 3000 lb load at 8 ft to the right of A and also at C (see figure). The uniform load includes an allowance for the weight of the beam. The allowable
> Solve the preceding problem if b = 225 mm, εx = 845 × 1026, and εy = 211 × 1026. Data from Problem 7: A thin square plate in biaxial stress is subjected to stresses σx and σy, a
> A thin square plate in biaxial stress is subjected to stresses σx and σy, as shown in part a of the figure. The width of the plate is b = 12.0 in Measurements show that the normal strains in the x and y directions are ε
> An element of material in plain strain has the following strains: εx = 0.002 and εy = 0.0015. (a) Determine the principal strains of the element. (b) Determine the maximum shear strain of the element. Confirm the solution using
> An element of material in plain strain has the following strains: εx = -0.001 5 and εy = 0.0015. (a) Determine the strains for an element oriented at an angle θ = 25°. (b) Find the principal strains of th
> An element of aluminum is subjected to triaxial stresses. Calculate the strains in the element in x, y, and z directions if the stresses σx, σy, and σz are –2000 psi, 3500 psi, and 2700 psi, respectively
> A bridge girder AB on a simple span of length L = 14 m supports a distributed load of maximum intensity q at mid-span and minimum intensity q/2 at supports A and B that includes the weight of the girder (see figure). The girder is constructed of three pl
> An element in uniaxial stress is subjected to tensile stresses σx = 14,250 psi, as shown in the figure. Using Mohr’s circle, determine the following. (a) The stresses acting on an element oriented at a counterclockwise angle
> The stresses acting on an element are σx = 750 psi, σy = 600 psi, and τxy = 400 psi. Determine the principal stresses and show them on a sketch of a properly oriented element. To
> A rectangular plate of dimensions 125 mm × 75 mm is subjected to tensile stress σx = 67 kPa and compressive stress σy. If it is known that the normal stress along the diagonal t–t is σt = &a
> At a point on the web of a girder on an overhead bridge crane in a manufacturing facility, the stresses are known to be σx = -4300 psi, σy = 1700 psi, and τxy = 3100 psi. A stress element located at the same point in the
> The surface of an airplane wing is subjected to plane stress with normal stresses σx and σy and shear stress τxy, as shown in the figure. At a counterclockwise angle θ = 32° from the x axis, the no
> A gusset plate on a truss bridge is in plane stress with normal stresses σx and σy and shear stress Ï„xy, as shown in the figure. At counterclockwise angles θ = 32° and θ = 78Â&de
> Solve the preceding problem for the element shown in the figure. Data from Problem 21: An element in plane stress from the frame of a racing car is oriented at a known angle θ (see figure). On this inclined element, the normal and shear s
> An element in plane stress from the frame of a racing car is oriented at a known angle θ (see figure). On this inclined element, the normal and shear stresses have the magnitudes and directions shown in the figure. Determine the normal and s
> Solve the preceding problem for σx = 11 MPa and σy = -20 MPa (see figure). Data from Problem 19: At a point on the surface of an elliptical exercise machine, the material is in biaxial stress with sx = 1400 psi and σy
> A cantilever beam AB of length L = 6.5 ft supports a trapezoidal distributed load of peak intensity q, and minimum intensity q/2, that includes the weight of the beam (see figure). The beam is a steel W12 × 14 wide-flange shape. Calculate th
> At a point on the surface of an elliptical exercise machine, the material is in biaxial stress with σx = 1400 psi and σy = -900 psi, as shown in the figure part a. The figure part b shows an inclined plane aa cut through the same po
> Repeat the previous problem using σx = 12 MPa. Data from Problem 17: A simply supported beam is subjected to point load P at mid-span. The normal stress on an element at mid-span is known to be σx = 1.5 ksi. Determine the element
> A simply supported beam is subjected to point load P at mid-span. The normal stress on an element at mid-span is known to be σx = 1.5 ksi. Determine the element stresses if it is rotated through angle θ = -45°. Show the
> Solve the preceding problem for a plate of dimensions 100 mm × 250 mm subjected to a compressive stress of -2.5 MPa in the long direction and a tensile stress of 12.0 MPa in the short direction (see figure). Data from Problem 15: A rectan
> A rectangular plate of dimensions 3.0in. × 5.0 in is formed by welding two triangular plates (see figure). The plate is subjected to a tensile stress of 500 psi in the long direction and a compressive stress of 350 psi in the short direction
> Repeat the previous problem using θ = -40° and stresses on the rotated element: σx1 = 70 MPa, σy1 = -82 MPa, and τx1y1 = -35 MPa. Data from Problem 13: Two steel rods are welded together (see fi
> Two steel rods are welded together (see figure); the seam is oriented at angle θ = -40°. The stresses on the rotated element are σx1 = 10 ksi, σy1 = -12 ksi, and τx1y1 = -5 ksi. Find the state of p
> Solve the preceding problem if the normal and shear stresses acting on the element are σx = 2100 kPa, σy = 300 kPa, and τxy = -560 kPa, and the seam is oriented at an angle of 22.5° to the element. Data from
> The polyethylene liner of a settling pond is subjected to stresses σx = 350 psi, σy = 112 psi, and τxy = 120 psi, as shown by the plane-stress element in the figure part a. Determine the normal and shear stresses acting o
> Solve the preceding problem if the normal and shear stresses acting on element B are -56 MPa, -17 MPa, and 27 MPa (in the directions shown in the figure) and the angle is 40° (clockwise). Data from Problem 9: The stresses acting on element
> Dimensions of cross section: b = 120 mm, t = 7mm, h = 350 mm, h1 = 330 mm, and V = 60 kN. Data for Problem 6: A wide-flange beam (see figure) is subjected to a shear force V. Using the dimensions of the cross section, calculate the moment of inertia an
> The stresses acting on element B (see figure part a) on the web of a wide-flange beam are found to be -14,500 psi in compression in the horizontal direction and -2530 psi in compression in the vertical direction (see figure part b). Also, shear stresses
> An element in plane stress on the fuselage of an airplane (figure part a) is subjected to compressive stresses with a magnitude of 42 MPa in the horizontal direction and tensile stresses with a magnitude of 9.5 MPa in the vertical direction (see figure p
> The cross section of an unbalanced wide flange beam is shown in the figure. Derive the following formula for the distance h1 from the centerline of one flange to the shear center S: Also, check the formula for the special cases of a T-beam (b2 = t2 = 0)
> Calculate the distance e from the centerline of the web of a C 310 × 45 channel section to the shear center S (see figure). Note: For purposes of analysis, consider the flanges to be rectangles with thickness tf equal to the average flange t
> Determine the plastic moment MP for a beam having the cross section shown in the figure if σY = 210 MPa. 120 150 mm mm Z- 250 mm 30 mm
> A wide-flange beam with an unbalanced cross section has the dimensions shown in the figure. Determine the plastic moment MP if σY = 36 ksi. 10 in. 0.5 in. z- 7 in. 0.5 in. 0.5 in. -5 in. -
> A singly symmetric beam with a T-section (see figure) has cross-sectional dimensions b = 140 mm, a = 190.8mm, tw = 6.99 mm, and tf = 11.2mm. Calculate the plastic modulus Z and the shape factor f. a
> A W 10 × 60 wide-flange beam is subjected to a bending moment M of such magnitude that the flanges yield but the web remains linearly elastic. (a) Calculate the magnitude of the moment M if the yield stress is σY = 36 ksi. (b) What percent of the moment
> Solve the preceding problem for a box beam with dimensions h = 400 mm, h1 = 360 mm, b = 200 mm, and b1 = 160 mm, and with yield stress σY = 220 MPa. Data from Problem 15: The hollow box beam shown in the figure is subjected to a bending mom
> Wide-flange shape, W18 × 71; V = 21 k. Data for Problem 5: A wide-flange beam (see figure) is subjected to a shear force V. Using the dimensions of the cross section, calculate the moment of inertia and then determine the following quantit
> The hollow box beam shown in the figure is subjected to a bending moment M of such magnitude that the flanges yield but the webs remain linearly elastic. (a) Calculate the magnitude of the moment M if the dimensions of the cross section are h = 15 in ,h1
> Solve the preceding problem for a box beam with dimensions h = 200 mm, h1 = 160 mm, b = 150 mm, and b1 = 130 mm. Assume that the beam is constructed of steel with yield stress σY = 220 MPa. Data from Problem 13: A hollow box beam with heigh
> A hollow box beam with height h = 9.5 in, inside height h1 = 8.0 in, width b = 5.25 in, and inside width b1 = 4.5 in is shown in the figure. Assuming that the beam is constructed of steel with yield stress σY = 42 ksi, calculate the yield mome
> Solve the preceding problem for a box beam with dimensions h = 0.5 m, b = 0.18 m, and t = 22 mm. The yield stress of the steel is 210 MPa. Data from Problem 11: A hollow box beam with height h = 16 in, width b = 8 in, and constant wall thickness t = 0
> A hollow box beam with height h = 16 in, width b = 8 in, and constant wall thickness t = 0.75 in is shown in the figure. The beam is constructed of steel with yield stress σY = 32 ksi. Determine the yield moment MY, plastic moment MP, and shap
> Solve the preceding problem for a W 410 × 85 wide-flange beam. Assume that σY = 250 MPa. Obtain the cross-sectional dimensions and section modulus of the beam in Appendix F. Data from Problem 9: Determine the yield moment MY, plastic moment MP, and sha
> Determine the yield moment MY, plastic moment MP, and shape factor f for a W 16 × 100 wide-flange beam if σY = 36 ksi. Obtain the cross- sectional dimensions and section modulus of the beam in Appendix F.
> Solve the preceding problem for a W 250 × 89 wide-flange beam. Obtain the cross- sectional dimensions and section modulus of the beam in Appendix F. Data from Problem 7: Determine the plastic modulus Z and shape factor f for a W 12 × 14 wide-flange bea
> (a) Determine the shape factor f for a hollow circular cross section having inner radius r1 and outer radius r2 (see figure). (b) If the section is very thin, what is the shape factor? z-
> Determine the shape factor f for a cross section in the shape of a double trapezoid having the dimensions shown in the figure. Also, check your result for the special cases of a rhombus (b1 = 0) and a rectangle (b1 = b2) Z-
> Dimensions of cross section: b = 220 mm, t = 12 mm, h = 600 mm, h1 = 570 mm, and V = 200 kN. Data for Problem 4: A wide-flange beam (see figure) is subjected to a shear force V. Using the dimensions of the cross section, calculate the moment of inertia
> The beams shown in the figure are subjected to bending moments M = 250 Nm? Each beam has a rectangular cross section with height h = 44 mm and width b = 10 mm (perpendicular to the plane of the figure). (a) For the beam with a hole at mid height, determi
> Calculate the distance e from the centerline of the web of a C 15 × 40 channel section to the shear center S (see figure). Note: For purposes of analysis, consider the flanges to be rectangles with thickness tf equal to the average flange th
> A simple beam with a W 10 × 30 wide-flange cross section supports a uniform load of intensity q = 3.0 kips/ft on a span of length L = 12 ft (see figure). The dimensions of the cross section are h = 10.5 in, b = 5.81 in, tf = 0.510 in, and tw
> A beam with a channel section is subjected to a bending moment M having its vector at an angle θ to the z axis (see figure). Determine the orientation of the neutral axis and calculate the maximum tensile stress σt and maximum com
> A beam with a rectangular cross section supports an inclined load P having its line of action along a diagonal of the cross section (see figure). Show that the neutral axis lies along the other diagonal. y h b-
> Repeat Problem 6.2-17 but now use a transformed-section approach. Data from Problem 6.2-17: Repeat Problem 1 but now assume that the steel plate is smaller (0.5 in. × 5 in.) and is aligned with the top of the beam as shown in the figure.
> Repeat Problem 1 but now assume that the steel plate is smaller (0.5 in. × 5 in.) and is aligned with the top of the beam as shown in the figure. Data from Problem 1: A composite beam is constructed using a steel plate (0.5 in. Ã&#
> A wood beam in a historic theater is reinforced with two angle sections at the outside lower corners (see figure). If the allowable stress in the wood is 12 MPa and that in the steel is 140 MPa, what is ratio of the maximum permissible moments for the be
> A composite beam is constructed from a wood beam (3 in. × 6 in.) and a steel plate (3 in. wide). The wood and the steel are securely fastened to act as a single beam. The beam is subjected to a positive bending moment Mz = 75 kip-in. Calcula
> A simply supported composite beam with a 3.6 m span supports a triangularly distributed load of peak intensity q0 at mid-span (see figure part a). The beam is constructed of two wood joists, each 50 mm × 280 mm, fastened to two steel plates,
> A simply supported wooden I-beam with a 12-ft span supports a distributed load of intensity q = 90 lb/ft over its length (see figure part a). The beam is constructed with a web of Douglas-fir plywood and flanges of pine glued to the web, as shown in the
> Wide-flange shape, W8 × 28; V = 10 k. Data for Problem 3: A wide-flange beam (see figure) is subjected to a shear force V. Using the dimensions of the cross section, calculate the moment of inertia and then determine the following quantiti
> A simply supported composite beam 3 m long carries a uniformly distributed load of intensity q = 30 kN/m (see figure). The beam is constructed of a wood member, 100 mm wide by 150 mm deep, and is reinforced on its lower side by a steel plate 8 mm thick a
> A bimetallic beam used in a temperature- control switch consists of strips of aluminum and copper bonded together as shown in the figure, which is a cross-sectional view. The width of the beam is 1.0 in., and each strip has a thickness of 1/16 in. Under
> The cross section of a sandwich beam consisting of fiberglass faces and a lightweight plastic core is shown in the figure. The width b of the beam is 50 mm, the thickness t of the faces is 4 mm, and the height hc of the core is 92 mm (total height h = 10
> The cross section of a sandwich beam consisting of aluminum alloy faces and a foam core is shown in the figure. The width b of the beam is 8.0 in., the thickness t of the faces is 0.25 in., and the height hc of the core is 5.5 in. (total height h = 6.0 i
> A plastic-lined steel pipe has the cross- sectional shape shown in the figure. The steel pipe has an outer diameter d3 = 100 mm and an inner diameter d2 = 94 mm. The plastic liner has an inner diameter d1 = 82 mm. The modulus of elasticity of the steel i
> A beam with a guided support and 10-ft span supports a distributed load of intensity q = 660 lb/ft over its first half (see figure part a) and a moment Mo = 300 ft-lb at joint B. The beam consists of a wood member (nominal dimensions 6 in. ×
> A round titanium tube of outside diameter d2 and a copper core of diameter d1 are bonded to form a composite beam, as shown in the figure. (a) Derive formulas for the allowable bending moment M that can be carried by the beam based upon an allowable stre
> A hollow box beam is constructed with webs of Douglas-fir plywood and flanges of pine, as shown in the figure in a cross-sectional view. The plywood is 1 in. thick and 12 in. wide; the flanges are 2 in. × 4 in. (nominal size). The modulus of
> A wood beam with cross-sectional dimensions 200 mm × 300 mm is reinforced on its sides by steel plates 12 mm thick (see figure). The moduli of elasticity for the steel and wood are Es = 190 GPa and Ew = 11 GPa, respectively. Also, the corres
> A composite beam consisting of fiberglass faces and a core of particle board has the cross section shown in the figure. The width of the beam is 2.0Â in., the thickness of the faces is 0.10 in., and the thickness of the core is 0.50 in. The be
> Dimensions of cross section: b = 180 mm, t = 12 mm, h = 420 mm, h1 = 380 mm, and V = 125 kN. Data for Problem 2: A wide-flange beam (see figure) is subjected to a shear force V. Using the dimensions of the cross section, calculate the moment of inertia
> A wood beam is strengthened using two steel plates as shown in Fig. a. The beam has simple supports and an overhang and is subjected to a point load and a uniform load as shown in Fig. b. Calculate the maximum tensile and compressive stresses
> A composite beam is constructed using a steel plate (0.5 in. × 6 in.) with two wood beams (3 in. × 6 in.) on either side. The wood and steel are securely fastened to act as a single beam. The beam is subjected to a positive bend
> A wood beam reinforced by an aluminum channel section is shown in the figure. The beam has a cross section of dimensions 150 mm × 250 mm, and the channel has a uniform thickness of 6.5 mm. If the allowable stresses in the wood and aluminum a
> A wood beam reinforced using two channels is subjected to a positive bending moment Mz = 25 kip-ft. Calculate the largest tensile and compressive stresses in the wood and steel if Ew = 1500 ksi and Es = 30,000 ksi. C 8 x 11.5 Neutral hi 4 in. axis 1
> A reinforced concrete slab (see figure) is reinforced with 13-mm bars spaced 160 mm apart at d = 105 mm from the top of the slab. The modulus of elasticity for the concrete is Ec = 25 GPa, while that of the steel is Es = 200 GPa. Assume that allowable st
> A reinforced concrete T-beam (see figure) is acted on by a positive bending moment of M = 175 kip-ft. Steel reinforcement consists of four bars of 1.41-inch diameter. The modulus of elasticity for the concrete is Ec = 3000 ksi while that of the steel is
> A reinforced concrete beam (see figure) is acted on by a positive bending moment of M = 160 kN m? Steel reinforcement consists of 4Â bars of 28 mm diameter. The modulus of elasticity for the concrete is Ec = 25 GPa while that of the steel is E
> A W 12 × 50 steel wide-flange beam and a segment of a 4-inch thick concrete slab (see figure) jointly resist a positive bending moment of 95 kip-ft. The beam and slab are joined by shear connectors that are welded to the steel beam. (These c
> The cross section of a bimetallic strip is shown in the figure. Assuming that the moduli of elasticity for metals A and B are EA = 168 GPa and EB = 90 GPa, respectively, determine the smaller of the two section moduli for the beam. (Recall that section m

