Question: The following is a portion of a
The following is a portion of a classic data set called the “pilot plot data†in Fitting Equations to
Data by Daniel and Wood, published in 1971. The response y is the acid content of material produced by titration, whereas the regressor x is the organic acid content produced by extraction and weighing.
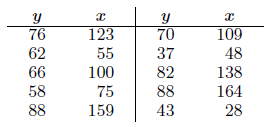
(a) Plot the data; does it appear that a simple linear regression will be a suitable model?
(b) Fit a simple linear regression; estimate a slope and intercept.
(c) Graph the regression line on the plot in (a).
Transcribed Image Text:
76 123 70 109 62 55 37 48 66 100 82 138 58 75 88 164 28 88 159 43
> Define the audit risk model and explain each term in the model
> Describe the three main techniques used to manipulate revenue.
> How do the COSO principles help an organization assess whether internal controls are designed and operating effectively?
> What are the three ways auditors respond to fraud risks?
> Why is an auditor’s independence so essential?
> Describe the types of procedures that constitute risk assessment procedures.
> At what two levels does the auditor assess the risk of material misstatement?
> What is the purpose of the Principles of Professional Conduct? Identify the six principles.
> Explain the difference between known and likely misstatements. Assume the auditor tests a sample of $100,000 of inventory and finds misstatements totaling $5,000. What is the likely misstatement if the account balance is $500,000?
> Explain the five elements that are part of a strategic understanding of the client’s business.
> What are the auditor’s possible defenses against lawsuits filed under the Securities Exchange Act of 1934?
> Explain the concept of professional skepticism and identify its two elements.
> What are the four major sources of auditors’ legal liability?
> Describe whether the auditor is more concerned about the occurrence or completeness objective related to cash receipts.
> What three types of authorizations are commonly used as internal controls for sales? Explain the importance of each.
> What are the purposes of the opinion section in the auditor’s report? Identify the most important information included in the opinion section.
> As part of the engagement team for the audit of JA Tire Manufacturing for the year ended December 31, 2019, you are responsible for auditing the sales and collection cycle. If you have not done so already, visit the textbook website to download the data
> A study was made to determine whether more Italians than Americans prefer white champagne to pink champagne at weddings. Of the 300 Italians selected at random, 72 preferred white champagne, and of the 400 Americans selected, 70 preferred white champagne
> A geneticist is interested in the proportions of males and females in a population who have a certain minor blood disorder. In a random sample of 100 males, 31 are found to be afflicted, whereas only 24 of 100 females tested have the disorder. Can we con
> State the null and alternative hypotheses to be used in testing the following claims and determine generally where the critical region is located: (a) The mean snowfall at Lake George during the month of February is 21.8 centimeters. (b) No more than 20%
> In a study to estimate the proportion of wives who regularly watch soap operas, it is found that 52 of 200 wives in Denver, 31 of 150 wives in Phoenix, and 37 of 150 wives in Rochester watch at least one soap opera. Use a 0.05 level of significance to te
> A survey was conducted in two Virginia cities to determine voter sentiment about two gubernatorial candidates in an upcoming election. Five hundred voters were randomly selected from each city and the following data were recorded: At the 0.05 level of
> A survey was conducted in Indiana, Kentucky, and Ohio to determine the attitude of voters concerning school busing. A poll of 200 voters from each of these states yielded the following results: At the 0.05 level of significance, test the null hypothesi
> To determine current attitudes about prayer in public schools, a survey was conducted in four Virginia counties. The following table gives the attitudes of 200 parents from Craig County, 150 parents from Giles County, 100 parents from Franklin County, an
> A college infirmary conducted an experiment to determine the degree of relief provided by three cough remedies. Each cough remedy was tried on 50 students and the following data recorded: Test the hypothesis that the three cough remedies are equally ef
> The following responses concerning the standard of living at the time of an independent opinion poll of 1000 households versus one year earlier seem to be in agreement with the results of a study published in Across the Board (June 1981): Test the hypo
> According to a Johns Hopkins University study published in the American Journal of Public Health, widows live longer than widowers. Consider the following survival data collected on 100 widows and 100 widowers following the death of a spouse: Can we co
> A study was made by a retail merchant to determine the relation between weekly advertising expenditures and sales. (a) Plot a scatter diagram. (b) Find the equation of the regression line to predict weekly sales from advertising expenditures. (c) Estim
> A criminologist conducted a survey to determine whether the incidence of certain types of crime varied from one part of a large city to another. The particular crimes of interest were assault, burglary, larceny, and homicide. The following table shows th
> A random sample of 200 married men, all retired, was classified according to education and number of children: Test the hypothesis, at the 0.05 level of significance, that the size of a family is independent of the level of education attained by the fa
> A random sample of 90 adults is classified according to gender and the number of hours of television watched during a week: Use a 0.01 level of significance and test the hypothesis that the time spent watching television is independent of whether the v
> In an experiment to study the dependence of hypertension on smoking habits, the following data were taken on 180 individuals: Test the hypothesis that the presence or absence of hypertension is independent of smoking habits. Use a 0.05 level of signifi
> For Exercise 1.19 on page 31, test the goodness of fit between the observed class frequencies and the corresponding expected frequencies of a normal distribution with μ = 1.8 and σ = 0.4, using a 0.01 level of significance. Exer
> For Exercise 1.18 on page 31, test the goodness of fit between the observed class frequencies and the corresponding expected frequencies of a normal distribution with μ = 65 and σ = 21, using a 0.05 level of significance. Exerci
> A coin is thrown until a head occurs and the number X of tosses recorded. After repeating the experiment 256 times, we obtained the following results: Test the hypothesis, at the 0.05 level of significance, that the observed distribution of X may be fi
> Three marbles are selected from an urn containing 5 red marbles and 3 green marbles. After the number X of red marbles is recorded, the marbles are replaced in the urn and the experiment repeated 112 times. The results obtained are as follows: Test the
> A die is tossed 180 times with the following results: Is this a balanced die? Use a 0.01 level of significance. 1 2 3 4 f 28 36 36 30 27 23
> The grades in a statistics course for a particular semester were as follows: Test the hypothesis, at the 0.05 level of significance, that the distribution of grades is uniform. Grade A в с D F 14 18 32 20 16
> A mathematics placement test is given to all entering freshmen at a small college. A student who receives a grade below 35 is denied admission to the regular mathematics course and placed in a remedial class. The placement test scores and the final grade
> A machine is supposed to mix peanuts, hazelnuts, cashews, and pecans in the ratio 5:2:2:1. A can containing 500 of these mixed nuts was found to have 269 peanuts, 112 hazelnuts, 74 cashews, and 45 pecans. At the 0.05 level of significance, test the hypot
> Hydrocarbon emissions from cars are known to have decreased dramatically during the 1980s. A study was conducted to compare the hydrocarbon emissions at idling speed, in parts per million (ppm), for automobiles from 1980 and 1990. Twenty cars of each mod
> An experiment was conducted to compare the alcohol content of soy sauce on two different production lines. Production was monitored eight times a day. The data are shown here. Production line 1: 0.48 0.39 0.42 0.52 0.40 0.48 0.52 0.52 Production line 2
> Two types of instruments for measuring the amount of sulfur monoxide in the atmosphere are being compared in an air-pollution experiment. Researchers 370 Chapter 10 One- and Two-Sample Tests of Hypotheses wish to determine whether the two types of instru
> With reference to Exercise 10.39 on page 358, test the hypothesis that σ21 = σ22 against the alternative that σ21 = σ22, where σ21 and σ22 are the variances for the running times of films
> For Exercise 10.41 on page 358, test the hypothesis at the 0.05 level of significance that σ21 = σ22 against the alternative that σ21 = σ22, where σ21 and σ22 are the variances of the numb
> A study is conducted to compare the lengths of time required by men and women to assemble a certain product. Past experience indicates that the distribution of times for both men and women is approximately normal but the variance of the times for women i
> Large-Sample Test of σ2 = σ20: When n ≥ 30, we can test the null hypothesis that σ2 = σ20, or σ = σ0, by computing which is a value of a random variable whose sampling d
> A soft-drink dispensing machine is said to be out of control if the variance of the contents exceeds 1.15 deciliters. If a random sample of 25 drinks from this machine has a variance of 2.03 deciliters, does this indicate at the 0.05 level of significanc
> Past data indicate that the amount of money contributed by the working residents of a large city to a volunteer rescue squad is a normal random variable with a standard deviation of $1.40. It has been suggested that the contributions to the rescue squad
> Aflotoxins produced by mold on peanut crops in Virginia must be monitored. A sample of 64 batches of peanuts reveals levels of 24.17 ppm, on average, with a variance of 4.25 ppm. Test the hypothesis that σ2 = 4.2 ppm against the alternative that σ2 = 4.2
> Past experience indicates that the time required for high school seniors to complete a standardized test is a normal random variable with a standard deviation of 6 minutes. Test the hypothesis that σ = 6 against the alternative thatσ < 6 if a random samp
> The content of containers of a particular lubricant is known to be normally distributed with a variance of 0.03 liter. Test the hypothesis that σ2 = 0.03 against the alternative that σ2 = 0.03 for the random sample of 10 containers in Exercise 10.23 on
> Show the necessary steps in converting the equation to the equivalent form b1 t = ryn-2 V1-r2
> Suppose that an experimenter postulates a model of the type Yi = β0 + β1x1i + €i i= 1, 2, . . . , n, when in fact an additional variable, say x2, also contributes linearly to the response. The true model is then g
> In Review Exercise 11.62, the student was required to show that simple linear regression model. Does the same hold for a model with zero intercept? Show why or why not. Exercise 11.62: Show, in the case of a least squares fit to the simple linear regr
> Consider the situation of Review Exercise 11.62 but suppose n = 2 (i.e., only two data points are available). Give an argument that the least squares regression line will result in (y1 − ˆy1) = (y2 − Ë&
> Show, in the case of a least squares fit to the simple linear regression model Yi = β0 + β1xi + €i, i= 1, 2, . . . , n, that E (4. – ŷ.) = E es = 0. i=1 1=1
> For a simple linear regression model Yi = β0 + β1xi + €i, i= 1, 2, . . . , n, where the i are independent and normally distributed with zero means and equal variances σ2, show that ¯ Y and
> Assuming that the i are independent and normally distributed with zero means and common variance σ2, show that B0, the least squares estimator of β0 in μY |x = β0 + β1x, is normally distributed
> In a certain type of metal test specimen, the normal stress on a specimen is known to be functionally related to the shear resistance. The following is a set of coded experimental data on the two variables: (a) Estimate the regression line Î&frac
> For the simple linear regression model, prove that E(s2) = σ2.
> Suppose a scientist postulates a model Yi = β0 + β1xi + €i, i = 1, 2, . . . , n, and β0 is a known value, not necessarily zero. (a) What is the appropriate least squares estimator of β1? Justify your answer. (b) What is the variance of the slope estimat
> Physical fitness testing is an important aspect of athletic training. A common measure of the magnitude of cardiovascular fitness is the maximum volume of oxygen uptake during strenuous exercise. A study was conducted on 24 middle-aged men to determine t
> Observations on the yield of a chemical reaction taken at various temperatures were recorded as follows: (a) Plot the data. (b) Does it appear from the plot as if the relationship is linear? (c) Fit a simple linear regression and test for lack of fit.
> Consider the vehicle data from Consumer Reports in Figure 11.30 on page 440. Weight is in tons, mileage in miles per gallon, and drive ratio is also indicated. A regression model was fitted relating weight x to mileage y. A partial SAS printout in Figure
> The business section of the Washington Times in March of 1997 listed 21 different used computers and printers and their sale prices. Also listed was the average hover bid. Partial results from regression analysis using SAS software are shown in Figure 11
> The following data represent the chemistry grades for a random sample of 12 freshmen at a certain college along with their scores on an intelligence test administered while they were still seniors in high school. (a) Compute and interpret the sample co
> An experiment was designed for the Department of Materials Engineering at Virginia Tech to study hydrogen embrittlement properties based on electrolytic hydrogen pressure measurements. The solution used was 0.1 N NaOH, and the material was a certain type
> With reference to Exercise 11.9 on page 399, construct (a) a 95% confidence interval for the average weekly sales when $45 is spent on advertising; (b) a 95% prediction interval for the weekly sales when $45 is spent on advertising. Exercise 11.9: A stu
> The amounts of solids removed from a particular material when exposed to drying periods of different lengths are as shown. (a) Estimate the linear regression line. (b) Test at the 0.05 level of significance whether the linear model is adequate. x (
> A study was made on the amount of converted sugar in a certain process at various temperatures. The data were coded and recorded as follows: (a) Estimate the linear regression line. (b) Estimate the mean amount of converted sugar produced when the code
> The Statistics Consulting Center at Virginia Tech analyzed data on normal woodchucks for the Department of Veterinary Medicine. The variables of interest were body weight in grams and heart weight in grams. It was desired to develop a linear regression e
> With reference to Exercise 11.8 on page 399, construct (a) a 95% confidence interval for the average course grade of students who make a 35 on the placement test; (b) a 95% prediction interval for the course grade of a student who made a 35 on the placem
> The following data were obtained in a study of the relationship between the weight and chest size of infants at birth. (a) Calculate r. (b) Test the null hypothesis that ρ = 0 against the alternative that ρ > 0 at the 0.01 leve
> Test the hypothesis that ρ = 0 in Exercise 11.43 against the alternative that ρ = 0. Use a 0.05 level of significance. Exercise 11.43: Compute and interpret the correlation coefficient for the following grades of 6 students selected at random: Mathemat
> With reference to Exercise 11.13 on page 400, assume a bivariate normal distribution for x and y. (a) Calculate r. (b) Test the null hypothesis that ρ = −0.5 against the alternative that ρ (c) Determine the percent
> With reference to Exercise 11.1 on page 398, assume that x and y are random variables with a bivariate normal distribution. (a) Calculate r. (b) Test the hypothesis that ρ = 0 against the alternative that ρ = 0 at the 0.05 level of
> Compute and interpret the correlation coefficient for the following grades of 6 students selected at random: Mathematics grade 70 92 80 74 65 83 English grade 74 84 63 87 78 90
> For a particular variety of plant, researchers wanted to develop a formula for predicting the quantity of seeds (in grams) as a function of the density of plants. They conducted a study with four levels of the factor x, the number of plants per plot. Fou
> Evaluating nitrogen deposition from the atmosphere is a major role of the National Atmospheric Deposition Program (NADP), a partnership of many agencies. NADP is studying atmospheric deposition and its effect on agricultural crops, forest surface waters,
> It is of interest to study the effect of population size in various cities in the United States on ozone concentrations. The data consist of the 1999 population in millions and the amount of ozone present per hour in ppb (parts per billion). The data are
> The following data were collected to determine the relationship between pressure and the corresponding scale reading for the purpose of calibration. (a) Find the equation of the regression line. (b) The purpose of calibration in this application is to
> A regression model is desired relating temperature and the proportion of impurities passing through solid helium. Temperature is listed in degrees centigrade. The data are as follows: (a) Fit a linear regression model. (b) Does it appear that the propo
> Heat treating is often used to carburize metal parts such as gears. The thickness of the carburized layer is considered an important feature of the gear, and it contributes to the overall reliability of the part. Because of the critical nature of this fe
> Organophosphate (OP) compounds are used as pesticides. However, it is important to study their effect on species that are exposed to them. In the laboratory study Some Effects of Organophosphate Pesticides on Wildlife Species, by the Department of Fisher
> Transistor gain between emitter and collector in an integrated circuit device (hFE) is related to two variables (Myers, Montgomery and Anderson-Cook, 2009) that can be controlled at the deposition process, emitter drive-in time (x1, in minutes) and emitt
> The following data are a result of an investigation as to the effect of reaction temperature x on percent conversion of a chemical process y. (See Myers, Montgomery and Anderson-Cook, 2009.) Fit a simple linear regression, and use a lack-of-fit test to d
> Use an analysis-of-variance approach to test the hypothesis that β1 = 0 against the alternative hypothesis β1 = 0 in Exercise 11.5 on page 398 at the 0.05 level of significance. Exercise 11.5: A study was made on the amount of co
> Suppose we have a linear equation through the origin (Exercise 11.28) μY |x = βx. (a) Estimate the regression line passing through the origin for the following data: (b) Suppose it is not known whether the true regression shou
> Test for linearity of regression in Exercise 11.8 on page 399. Comment. Exercise 11.8: A mathematics placement test is given to all entering freshmen at a small college. A student who receives a grade below 35 is denied admission to the regular mathemat
> Test for linearity of regression in Exercise 11.3 on page 398. Use a 0.05 level of significance. Comment. Exercise 11.3: The amounts of a chemical compound y that dissolved in 100 grams of water at various temperatures x were recorded as follows: (a)
> For the data in Exercise 11.29, find a 95% prediction interval at x = 25.
> The amounts of a chemical compound y that dissolved in 100 grams of water at various temperatures x were recorded as follows: (a) Find the equation of the regression line. (b) Graph the line on a scatter diagram. (c) Estimate the amount of chemical tha
> Use the data set (a) Plot the data. (b) Fit a regression line through the origin. (c) Plot the regression line on the graph with the data. (d) Give a general formula (in terms of the yi and the slope b1) for the estimator of σ2. (e) Give a f
> There are important applications in which due to known scientific constraints, the regression line must go through the origin (i.e., the intercept must be zero). In other words, the model should read and only a simple parameter requires estimation. The
> Consider the regression of mileage for certain automobiles, measured in miles per gallon (mpg) on their weight in pounds (wt). The data are from Consumer Reports (April 1997). Part of the SAS output from the procedure is shown in Figure 11.13. (a) Estim
> With reference to Exercise 11.3 on page 398, use the value of s2 found in Exercise 11.19(a) to compute (a) a 99% confidence interval for the average amount of chemical that will dissolve in 100 grams of water at 50 â—¦ C; (b) a 99% pred
> Using the value of s2 found in Exercise 11.17(a), construct a 95% confidence interval for the amount of converted sugar corresponding to x = 1.6 in Exercise 11.5 on page 398. Exercise 11.17: With reference to Exercise 11.5 on page 398, (a) evaluate s2;
> Using the value of s2 found in Exercise 11.17(a), graph the regression line and the 95% confidence bands for the mean response μY |x for the data of Exercise 11.5 on page 398. Exercise 11.17: With reference to Exercise 11.5 on page 398, (a
> With reference to Exercise 11.6 on page 399, use the value of s2 found in Exercise 11.18(a) to compute (a) a 95% confidence interval for the mean shear resistance when x = 24.5; (b) a 95% prediction interval for a single predicted value of the shear resi

