Question: The least squares fit of polar bear
The least squares fit of polar bear weight to body length is obtained in Example 5. Taking skull length instead of body length, the summary statistics for y = weight and x = skull length, based on Table D.13 of the Data Bank, are
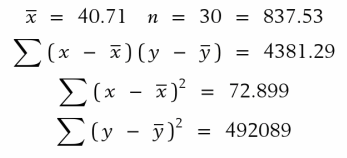
(a) Obtain the equation of the least squares regression line.
(b) Construct a 95% confidence interval for the slope.
(c) A polar b ear skull is found whose skull length = 44 cm when adjusted for missing skin, flesh, and hair. Find a 95% prediction interval for the weight of that polar bear.
> A genetic experiment is undertaken to study the competition between two types of female flies (Drosophila melanogaster) in cages with one male genotype acting as a substrate. The independent variable x is the time spent in cages, and the dependent variab
> An environmental scientist identified a point source for E. Coli at the edge of a stream. She then measured y = E. Coli, in colony forming units per I 00 ml of water, at different distances, in feet, downstream from the point source. Suppose she obtains
> Let X1 , … , Xn, be a random sample from a continuous population whose median is denoted by M. For testing H0 : M = M0, we can use the sign test statistic S = No. of Xi > M0, i = 1, ... , n. H0 is rejected at level a in favor of H1
> Evaluate: (a) Sign test statistic. (b) Signed-rank statistic.
> (a) Calculate Spearman's rank correlation for the data on Chester Whites. (b) Test for independence of calcium and phosphate levels using the rejection region. (c) What is the approximate level of significance?
> A mixture of compounds called phenolics occurs in wood waste products. It has been found that when phenolics are present in large quantities, the waste becomes unsuitable for use as a livestock feed. To compare two species of wood, a dairy scientist meas
> The city of Madison regularly checks the quality of water at swimming beaches located on area lakes. Fifteen times the concentration of fecal coliforms, in number of colony forming units (CFU) per 100 ml of water, was measured during the summer at one be
> In a study of the cognitive capacities of nonhuman primates, 19 monkeys of the same age are randomly divided into two groups of 10 and 9. The groups are trained by two different teaching methods to recollect an acoustic stimulus. The monkeys' scores on a
> Referring to Exercise 15.27, calculate: (a) The sign test statistic. (b) The significance probability when the alternative is that Judge 2 gives higher scores than Judge I. Data from Exercise 15.27: Five finalists in a figure-skating contest are rated
> Using Appendix B, Table 9, find: (a) P[ T+ ≥ 28 ] when n = 8. (b) P [ r+ ≤ 5 ] when n = 7. (c) The point c such that P [ T+ ≤ c ] is approximately .05 when n = 13.
> Five finalists in a figure-skating contest are rated by two judges on a 10-point scale as follows: Calculate the Spearman's rank correlation rSp between the two ratings.
> Using Appendix B, Table 8, find: (a) P [ Ws ≥ 42] when n1 = 5, n2 = 7. (b) P [ Ws ≤ 25 ] when n1 = 6, n2 = 6. (c) P[Ws ≥ 81 or Ws ≤ 4S ] when n1 = 10, n2 = 7. (d) The point c such
> Three male and three female students recorded the number of times they used a credit card in one week. Designate males as population A. Evaluate WA.
> Refer to the output here concerning the time (min) it took four different persons (blocks) to complete three different tasks. (a) Identify the SSE and its degrees of freedom. (b) Are the block means different? Check the calculation of F for blocks from
> Three different chemicals are compared on their ability to make fabric stain resistant. Four bolts of cloth , manufactured weeks apart, are used. Because the results are expected to vary from bolt of cloth to bolt, three small samples are cut from each b
> The iris data described in Example 6 are given in the stem-and-leaf diagrams below. The MINITAB output for the analysis of the iris data is given below. One-way ANOVA : (a) Identify the SSE and its degrees of freedom . Also locates. (b) Check the calcul
> Using the computer. MINITAB can be used for ANOVA. With the data from three treatments entered in columns 1-3 The Output is as follows: Use computer software to analyze the moisture data.
> A campus area merchant recorded the number of bad checks received per month, for five months 4 5 4 7 6 Calculate: (a) The sample variance. (b) The sample standard deviation.
> As part of the multilab study, four fabrics are tested for flammability at the National Bureau of Standards. The following burn times in seconds are recorded after a paper tab is ignited on the hem of a dress made of each fabric. (a) State the statistica
> Refer to the data on travel expenses and the F-test. It is the ordering of the population means, and the sizes of their differences, that is the key finding of study. (a) Calculate 95% simultaneous confidence intervals for the differences in means. (b)
> Compute the sums of squares and construct the ANOVA table for the data given in Exercise 14.31. Use software to verify your ANOVA table. Data from Exercise 14.31: Food scientists investigated whether making a cheese sauce by a continuous process or bat
> Food scientists investigated whether making a cheese sauce by a continuous process or batch process made any difference to taste. They also included a third treatment, a carefully selected ideal product, that served as a control. Treatment I is the ideal
> A large organization is being investigated to determine if its recruitment is sex-biased. Tables 15 and 16, respectively, show the classification of applicants for secretarial and for sales positions according to gender and result of interview. Table 17
> A random sample of 130 business executives was classified according to age and the degree of risk aversion as measured by a psychological test. Do these data demonstrate an association between risk aversion and age?
> By polling a random sample of 350 undergraduate students, a campus press obtains the following frequency counts regarding student attitude toward a proposed change in dormitory regulations. Are attitude toward the proposal and gender associated?
> In a study on the effect of diet and lifestyle on heart disease, 96 patients with severe coronary blockage were randomly assigned, 49 to an experimental group and 4 7 to a control group. The patients in the experimental group had a low-fat vegetarian die
> Using the data for drugs l and 3 in Exercise 13.33, make a 2 * 2 contingency table and test H0 : p1 = p3 versus H 1 : p1 ≠p3 at a = .05 employing: (a) The x2 test. (b) The Z test. Data from Exercise 13.33: To compare the effectivene
> To compare the effectiveness of four drugs in relieving postoperative pain, an experiment was done by randomly assigning 195 surgical patients to the drugs under study. Recorded here are the number of patients assigned to each drug and the number of pati
> Find the standard deviation of the measurements of diameters given in Exercise 2.45. Data from Exercise 2.45: The following measurements of the diameters (in feet) of Indian mounds in southern Wisconsin were gathered by examining reports in the Wisconsi
> Refer to the data in Exercise 13.31. (a) Use the Z test for testing the equality of two population proportions with a two-sided alternative. Verify the relation x2 = Z2 by comparing their numerical values. (b) If the alternative is that the incidence r
> Refer to Exercise 3.48 and the data concerning a vaccine for type B hepatitis. Do these data indicate that there is a different rate of incidence of hepatitis between the vaccinated and nonvaccinated participants? Use the x2 test for homogeneity in a con
> Referring to the data for site 3 and site 4 in Exercise 13.29, make a 2 * 2 table and test H0 : p3 = p4 versus H1 : p3 > p4 at a = .05. (a) Is there strong evidence that the probability a paper will be taken from the drop site is higher for site 3 th
> A community paper in the Spanish language was delivered to many sites in the San Francisco Bay area. As a check on the circulation numbers that are important to advertisers, a survey was conducted at four drop sites. The number of papers delivered to eac
> The following table records the observed number of births at a hospital in four consecutive quarterly periods. It is conjectured that twice as many babies are born during the Jan.-March quarter than any of the other three quarters. At 
> To examine the quality of a random number generator, frequency counts of the individual integers are recorded from an output of 500 integers. The concept of randomness implies that the integers 0, 1, . . . , 9 are equally likely. Based on the observed fr
> Refer to the physical conditioning data given in Data Bank. Use MINITAB or some other package to fit a regression of the final number of sit-ups on the initial number of sit-ups and the gender of the student.
> Recorded here are the scores x1 and x2 in two midterm examinations, the GPA x3, and the final examination score y for 20 students in a statistics class. (a) Ignoring the data of GPA and the first midterm score, fit a simple linear regression of y on x2.
> A forester seeking information on basic tree dimensions obtains the following measurements of the diameters 4.5 feet above the ground and the heights of 12 sugar maple trees ( courtesy of A. Ek). The forester wishes to determine if the diameter measureme
> Refer to the data of speed x and stopping distance y given in Table I. The MINITAB commands for fitting a straight line regression to y’ = √y and x are (a) Obtain the computer output and identify the equation of the fi
> In 20 17, there were eight skyscrapers in the world over 500 meters tall. The ordered heights are 508 530 541 555 594 601 632 828 (a) Calculate the sample variance for the eight skyscrapers. (b) Calculate the sample standard deviation. (c) Drop the lar
> Listed below are the price quotations on an Internet site for a midsize foreign used car along with their age and odometer mileage. Perform a multiple regression analysis of these data. In particular. (a) Determine the equation for predicting the price f
> Consider the data on male wolves in Table D.9 of the Data Bank concerning age (years) and canine length (mm). (a) Obtain the least squares fit of canine length to the predictor age. (b) Obtain the least squares fit of canine length to a quadratic functi
> An experimenter obtains the following residuals after fitting a quadratic expression in x. Do the basic assumptions appear to be violated?
> The following predicted values and residuals are obtained in an experiment conducted to determine the degree to which the yield of an important chemical in the manufacture of penicillin is dependent on sugar concentration (the time order of the experimen
> A second-degree polynomial y = β^o + β^1x + β^2x2 is fitted to a response y, and the following predicted values and residuals are obtained. Do the assumptions appear to be violated?
> Given the data, (a) Fit a quadratic curve using the equations on page 391. (b) Verify your answers using software.
> The data on the maximum height (feet) and top speed (mph) of the 12 highest roller coasters, displayed in the chapter opener, are (a) Use MINITAB or some other software program to determine the proportion of variation in speed due to regression on height
> Use MINITAB or some other software to obtain the scatter diagram, correlation coefficient, and the regression line of the final time to run 1.5 miles on the initial times given in the Data Bank.
> Use MINITAB or some other software program to regress the marine growth on freshwater growth for the fish growth data of the Data Bank. Do separate regression analyses for: (a) All fish. (b) Males. (c) Females. Your analysis should include (i) a scat
> For each data set, calculate s2. (a) 1 4 3 2 2 (b) -2 1 -1 - 3 0 -2 (c) 9 8 8 9 8 8 9
> Refer to Exercise 11.56 and a least squares fit using the data on all of the wolves in Table D.9 of the Data Bank concerning body length (cm) and weight (lb). There is one obvious outlier, row 18 with body length 123 and weight 106. Drop this observation
> Consider the data on all of the wolves in the Data Bank concerning body length ( cm) and weight (lb). Using MINITAB or some other software program: (a) Plot weight versus body length. (b) Obtain the least squares fit of weight to the predictor variable
> Consider the data on wolves in the Data Bank concerning body length (cm) and weight (lb). Calculate the correlation coefficient r and r2 for (a) All wolves. (b) Male wolves. (c) Female wolves. (d) Comment on the differences in your answers. Make a mu
> The calculations involved in a regression analysis become increasingly tedious with larger data sets. Access to a computer proves to be of considerable advantage. We repeat here a computer based analysis of linear regression using the data of Example 4 a
> Again referring to Exercise 11.51, find the sample correlation coefficient between age and selling price. What proportion of the variability in price is explained by the fitted straight line? Comment on the adequacy of the straight line fit. Data from E
> Refer to Exercise 11.51. (a) From the fitted regression line, determine the predicted value for the average selling price of a 5-year-old car and construct a 95% confidence interval. (b) Determine the predicted value for a 5-year-old car to be listed o
> A top Internet site features used cars for sale. The age, x, measured in years and the price, y, expressed in thousands of dollars were recorded from a sample of listings for a popular midsize foreign car. (a) Plot the scatter diagram. (b) Determine the
> Refer to Exercise 11.49. (a) Calculate the sample correlation coefficient. (b) What proportion of the y variability is explained by the fitted regression line? Data from Exercise 11.49: A recent graduate moving to a new job collected a sample of month
> A recent graduate moving to a new job collected a sample of monthly rent ( dollars) and size (square feet) of 2-bedroom apartments in one area of a Midwest city. (a) Plot the scatter diagram and find the least squares fit of a straight line. (b) Do thes
> Refer to Exercise 11.47. (a) Obtain the decomposition of the total y variability into two parts: one explained by linear relation and one not explained . (b) What proportion of the y variability is explained by the straight line regression? (c) Calcul
> A sample of six university students responded to the question "H ow much time, in minutes, did you spend on the social network site yesterday?" One student never used the site and was dropped from the study. 100 45 60 130 30 Calculate, using these five v
> Many college students obtain college degree credits by demonstrating their proficiency on exams developed as part of the College Level Examination Program (CLEP). Based on their scores on the College Qualification Test (CQT), it is helpful if students co
> Refer to Exercise 11.44. (a) Construct a 95% confidence interval for the slope of the regression line. (b) Obtain a 90% confidence interval for the expected y value corresponding to x = 4 days. Data from Exercise 11.44: Last week's total number of hou
> Refer to Exercise 11.44. (a) Find the residuals. (b) Calculate the SSE by (i) summing the squares of the residuals and also (ii) using the formula SSE = Syy – S2xy / Sxx. (c) Estimate the error variance. Data from Exercise 11.44: Las
> Last week's total number of hours worked by a student, y, depends on the number of days, x, he reported to work last week. Suppose the data from nine students provided (a) Plot the scatter diagram. (b) Calculate x, y, Sxx, Syy , and Sxy. (c) Determine t
> Concerns that were raised for the environment near a government facility led to a study of plants. Since leaf area is difficult to measure, the leaf area ( cm2 ) was fit to x = Leaf length * Leaf width using a least squares approach. For data collected
> Students can bike to a park on the other side of a lake by going around one side of the lake or the other. After much discussion about which was faster, they decided to perform an experiment. Among the 12 students available, 6 were randomly selected to f
> Two scales are available at a campus athletic facility. A student wonders if, on average, they give the same reading for weight. She and four others weigh themselves on both scales. The readings are (a) Find a 95% confidence interval for the mean differe
> A sample of river water is divided into two specimens. One is randomly selected to be sent to Lab A and the other is sent to Lab B. This is repeated for a total of nine times. The measurement of suspended solids at Lab B is subtracted from that of Lab A
> A driver is stopped for erratic driving, and the alcohol content of his blood is checked. Specify the sample space and the event A = [ level exceeds legal limit ] if the legal limit is .10%.
> Examine each of these probability assignments and state what makes it improper. (a) Concerning tomorrow's weather, P( Rain) = .4 P ( Cloudy but no rain) = . 5 P( Sunny) = .2 (b) Concerning your passing of the statistics course, P( Pass) = 1.1 P( Fa
> For the data of Exercise 2.57, calculate s2 by using the alternative formula. Data from Exercise 2.57: For the data set 6 2 4
> Identify these events in the corresponding parts of Exercise 4.95. (a) At most 7 commercials. (b) Less than 18 .5 hours. (c) At least 30% visited a site. Data from Exercise 4.95: Describe the sample space for each of the following experiments. (a) T
> In order to keep up with the demand for its new earphones, a manufacturer h ad to purchase a key p art from three different suppliers. Supplier l provides 15% of the parts and 10% are defective. Supplier 2 provides 60% of the parts and 4% are defective.
> Identity theft is a growing problem in the United States. According to a Federal Trade Commission Report about 280,000 identity complaints were filed in a recent year. Among the 43.2 million persons in the 20- 29 year old age group, 56,689 complaints wer
> An e-commerce electronics firm sent 80% of its orders by a parcel service that delivers late only 3% of the time. It sends the other 20% of items by a combination bus service and local transportation that delivers late 6% of the time. Find the (a) The p
> Refer to the Statistics in Context discussion about space junk. Change the probability of hitting to (a) .4 and repeat the calculation of probability for hitting your city. (b) .1 and repeat the calculation of probability for hitting your city.
> Mr. Hope, a character apprehended by Sherlock Holmes, was driven by revenge to commit two murders. He presented two seemingly identical pills, one containing a deadly poison, to an adversary who selected one while Mr. Hope took the other. The entire proc
> Refer to the probability t able given in Exercise 4.112 concerning three events A, B, and C. (a) Find the conditional probability of A given that B does not occur. (b) Find the conditional probability of B given that both A and C occur. (c) Determine
> Let A b e the event that a person is a binge drinker and B be the event that the person is female. For a person selected at random, a recent survey of the National Center for Health Statistics suggests the probabilities P(B) = .50 P(A IB) = .11 P(A IB)
> Refer to Exercise 4.118 for each pair of events given below, determine whether or not the events are independent. (a) A, C (b) AB,C Data from Exercise 4.118: Suppose three events A, B, and Care such that B and C are mutually exclusive and
> Suppose three events A, B, and Care such that B and C are mutually exclusive and (a) Show the events in a Venn diagram. (b) Determine the probabilities of all the intersections and mark them in the Venn diagram. (c) Find the probability that only one o
> Repeat (a) and (b) of Exercise 2.59 for the data set 2.5 1.7 2.1 1.5 1.7 Data from Exercise 2.59: For the data set 8 6 14 4 (a) Calculate the deviations (x - x) and check to see that they add up to 0. (b) Calculate the variance and the standard de
> Rap music was the favorite genre of 6 out of 56 students from a large Midwestern university. Identify a statistical population and the sample.
> Given P(AB) = .4 and P(B) = .5, find P(A IB). If, further, P(A) = .8, are A and B independent?
> Suppose a fair die has its even-numbered faces painted red and the odd-numbered faces are white. Consider the experiment of rolling the die once and the events A = [ 2 or 3 shows up ] B = [ Red face shows up ] Find the following probabilities: (a) P(A)
> Referring to Exercise 4.114 find the probability that: (a) B occurs and C does not occur. (b) At least one of the events A and B occurs . ( c) Exactly two of the events A , B, and C occur. Data from Exercise 4.114: Concerning three events A, B, and C
> Concerning three events A, B, and C, the following probabilities are specified. Draw a Venn diagram and determine the probabilities of all the intersections that appear in the diagram.
> Referring to Exercise 4.112 describe each event in the context of the problem and calculate the probabilities of the following events. (a) Both B and C occur. (b) Either B or C occurs. (c) B occurs and C does not occur. (d) Only one of the three even
> Let the three events A, B, and C represent the cases that a randomly selected student is good at answering multiple choice, essay, and mathematical questions, respectively. The probabilities of the various intersections are given in the accompanying tabl
> Using event relations, express the following events in terms of the three events A, B, and C. (a) All three events occur. (b) At least one of the three events occurs. (c) A and B occur and C does not. (d) Only B occurs.
> From the probabilities exhibited in this Venn diagram, find P(A), P(AB), P(B U C), and P(BC).
> Suppose each of the numbers .2, .4, and .6 represents the probability of one of the events A, AB, and A U B. Connect the probabilities to the appropriate events.
> Express the following statements in the notations of the event operations. (a) A occurs and B does not. (b) N either A nor B occurs. (c) Exactly one of the events A and B occurs.
> For the data set 8 6 14 4 (a) Calculate the deviations (x - x) and check to see that they add up to 0. (b) Calculate the variance and the standard deviation.
> In checking the conditions of a used car, let A denote the event that the car has a faulty transmission, B the event that it has faulty brakes, and C the event that it has a faulty exhaust system. Describe in words what the following events represent: (a
> A three-digit number is formed by arranging the digits 2, 4, and 5 in a random order. (a) List the sample space. (b) Find the probability of getting a number less than 400. (c) What is the probability that an even number is obtained?
> Does the uniform model apply to the following observations? Explain. (a) Day of week on which the most persons depart by airplane from Chicago. (b) Day of week on which the monthly low temperature occurs. (c) Day of week on which the maximum amount of
> Chevalier de Mere, a French nobleman of the seventeenth century, reasoned that in a single throw of a fair die, P ( 1 ) = 1/6, so in two throws, P ( l appears at least once ) = 1/6 + 1/6 = 1/3. What is wrong with the above reasoning?
> Refer to Exercise 4.102. Instead of a completely random choice, suppose a plot is chosen at random from each row and assigned to variety a. Find the probability that the plots receiving a are in the same column. Data from Exercise 4.102: To compare two

