Question: In a study on the effect of
In a study on the effect of diet and lifestyle on heart disease, 96 patients with severe coronary blockage were randomly assigned, 49 to an experimental group and 4 7 to a control group. The patients in the experimental group had a low-fat vegetarian diet, regular exercise, and stress management training, whereas those in the control group had a low-fat diet and moderate exercise. The condition of their coronary blockage was monitored throughout the study period, and the following results were noted.
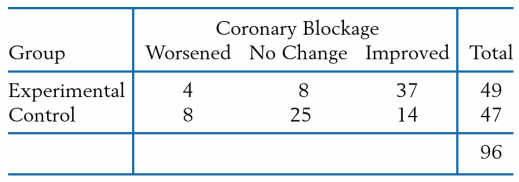
Analyze the data to determine if the changes in coronary blockage were significantly different between the two groups of patients.
> Referring to the earthquake data in Exercise 2.20, (a) Obtain a five-number summary: minimum, Q1, Q2, Q3, maximum. (b) Construct a boxplot. Data from Exercise 2.20: In a recent year, 35 sites around the world experienced earthquakes of magnitude great
> Refer to the data on throwing speed in Exercise 2.42. Make separate boxplots to compare males and females. Data from Exercise 2.42: Physical education researchers interested in the development of the overarm throw measured the horizontal velocity of a t
> Two cities provided the following information on public school teachers' salaries. (a) Construct a boxplot for the salaries in City A. (b) Construct a boxplot, on the same graph, for the salaries in City B. (c) Are there larger differences at the lower
> The weights ( oz) of nineteen babies born in Madison Wisconsin are summarized in the computer output. Obtain the z score for a baby weighing (a) 102 oz (b) 144 oz
> z-value of a measurement = Measurement - x¯ / s When two measurements originate from different sources, converting them to the z scale helps to draw a sensible interpretation of their relative magnitudes. For instance, suppose a student scored 65 in a ma
> Refer to the data on number of returns. (a) Calculate x and s. (b) Find the proportions of the observations that are in the intervals x ± s, x ± 2 s, and x ± 3 s. (c) Compare the results of part (b) with the empirical guidelines.
> Refer to the data on lizards in Exercise 2.19. (a) Calculate x ands. (b) Find the proportion of the observations that are in the intervals x ± s, x ± 2 s, and x ± 3 s. (c) Compare the results of part (b) with
> Which of the following are anecdotal and which are based on a sample? (a) Ellie told her friends that she is saving $31 a month because she changed to a prepaid cell phone. (b) One morning, among a large number of coffee shop patrons, the orders of 47 c
> Refer to the data on bone mineral content in Exercise 2.41. (a) Calculate x ands. (b) Find the proportion of the observations that are in the intervals x ± s, x ± 2 s, and x ± 3 s. (c) Compare the results of p
> Calculations with the test scores data of Exercise 2.22 give x = 150.125 and s = 24.677. (a) Find the proportion of the observations in the intervals x ± 2 s and x ± 3 s. (b) Compare your findings in part (a) with those su
> Should you be surprised if the range is larger than twice the interquartile range? Explain.
> For the extracurricular data of Exercise 2.3, calculate the interquartile range. Data from Exercise 2.3: A student at the University of Wisconsin surveyed 40 students in her dorm concerning their participation in extracurricular activities during the pa
> For the data set of Exercise 2.22, calculate the interquartile range. Data from Exercise 2.22: The following data represent the scores of 40 students on a college qualification test (courtesy of R. W. Johnson).
> 1. If a fixed number c is added to all measurements in a data set, the deviations ( x - x¯) remain unchanged. Consequently, s2 and s remain unchanged. 2. If all measurements in a data set are multiplied by a fixed number d, the deviations ( x - x) get
> The weights (oz) of nineteen babies born in Madison, Wisconsin, are summarized in the computer output. (a) Locate a measure of variation and also calculate the sample variance. (b) Calculate the interquartile range and interpret this value. (c) Give a v
> The monthly number of hours students spend doing community service are summarized in the computer output: (a) Locate a measure of variation and also calculate the sample variance. (b) Calculate the interquartile range and interpret this value. (c) Give
> The performance time (minutes) for Beethoven's Ninth Symphony is obtained from each of seven compact discs. 66.9 66.2 71.0 68.6 65.4 68.4 71.9 (a) Find the sample median. (b) Find the sample mean . (c) Find the sample standard deviation. (d) Use soft
> With reference to checked bags in Exercise 2.13, (a) Find the sample mean . (b) Find the sample standard deviation. Data from Exercise 2.13: A sample of 50 departing airline passengers at the main check-in counter produced the following number of bags
> About 42% of the members of a local hiking club own a dog. Should these people be considered as a random sample of dog ownership for persons living in the city7
> With reference to the data on the length of 10 major league baseball games in Exercise 2.43: (a) Find the sample mean. (b) Find the sample variance. (c) Find the sample standard deviation. Data from Exercise 2.43: On opening day one season, 10 major
> With reference to the radiation leakage data given in Exercise 2.15, calculate : (a) The sample variance. (b) The sample standard deviation. Data from Exercise 2.15: Before microwave ovens are sold, the manufacturer must check to ensure that the radia
> Refer to Exercise 12.16. The estimated standard errors of β1 and β2 are .0606 and .0632, respectively. (a) Obtain a 90% confidence interval for β1. (b) Test H0 : β2 = .5 versus H1 : β1 ≠ .5 with .05. Data from Exercise 12.16: Some researchers illust
> Some researchers illustrate a multiple linear regression equation to predict the yearly output of an oil field. We use their latest 20 years of data and change the units of three of their variables to y = loge (yearly output) where output is measured in
> Consider the data on a response variable and two predictor variables. (a) Fit a multiple regression model with response variable y. (b) Verify your answer using software.
> A genetic experiment is undertaken to study the competition between two types of female flies (Drosophila melanogaster) in cages with one male genotype acting as a substrate. The independent variable x is the time spent in cages, and the dependent variab
> An environmental scientist identified a point source for E. Coli at the edge of a stream. She then measured y = E. Coli, in colony forming units per I 00 ml of water, at different distances, in feet, downstream from the point source. Suppose she obtains
> Let X1 , … , Xn, be a random sample from a continuous population whose median is denoted by M. For testing H0 : M = M0, we can use the sign test statistic S = No. of Xi > M0, i = 1, ... , n. H0 is rejected at level a in favor of H1
> Evaluate: (a) Sign test statistic. (b) Signed-rank statistic.
> (a) Calculate Spearman's rank correlation for the data on Chester Whites. (b) Test for independence of calcium and phosphate levels using the rejection region. (c) What is the approximate level of significance?
> A mixture of compounds called phenolics occurs in wood waste products. It has been found that when phenolics are present in large quantities, the waste becomes unsuitable for use as a livestock feed. To compare two species of wood, a dairy scientist meas
> The city of Madison regularly checks the quality of water at swimming beaches located on area lakes. Fifteen times the concentration of fecal coliforms, in number of colony forming units (CFU) per 100 ml of water, was measured during the summer at one be
> In a study of the cognitive capacities of nonhuman primates, 19 monkeys of the same age are randomly divided into two groups of 10 and 9. The groups are trained by two different teaching methods to recollect an acoustic stimulus. The monkeys' scores on a
> Referring to Exercise 15.27, calculate: (a) The sign test statistic. (b) The significance probability when the alternative is that Judge 2 gives higher scores than Judge I. Data from Exercise 15.27: Five finalists in a figure-skating contest are rated
> Using Appendix B, Table 9, find: (a) P[ T+ ≥ 28 ] when n = 8. (b) P [ r+ ≤ 5 ] when n = 7. (c) The point c such that P [ T+ ≤ c ] is approximately .05 when n = 13.
> Five finalists in a figure-skating contest are rated by two judges on a 10-point scale as follows: Calculate the Spearman's rank correlation rSp between the two ratings.
> Using Appendix B, Table 8, find: (a) P [ Ws ≥ 42] when n1 = 5, n2 = 7. (b) P [ Ws ≤ 25 ] when n1 = 6, n2 = 6. (c) P[Ws ≥ 81 or Ws ≤ 4S ] when n1 = 10, n2 = 7. (d) The point c such
> Three male and three female students recorded the number of times they used a credit card in one week. Designate males as population A. Evaluate WA.
> Refer to the output here concerning the time (min) it took four different persons (blocks) to complete three different tasks. (a) Identify the SSE and its degrees of freedom. (b) Are the block means different? Check the calculation of F for blocks from
> Three different chemicals are compared on their ability to make fabric stain resistant. Four bolts of cloth , manufactured weeks apart, are used. Because the results are expected to vary from bolt of cloth to bolt, three small samples are cut from each b
> The iris data described in Example 6 are given in the stem-and-leaf diagrams below. The MINITAB output for the analysis of the iris data is given below. One-way ANOVA : (a) Identify the SSE and its degrees of freedom . Also locates. (b) Check the calcul
> Using the computer. MINITAB can be used for ANOVA. With the data from three treatments entered in columns 1-3 The Output is as follows: Use computer software to analyze the moisture data.
> A campus area merchant recorded the number of bad checks received per month, for five months 4 5 4 7 6 Calculate: (a) The sample variance. (b) The sample standard deviation.
> As part of the multilab study, four fabrics are tested for flammability at the National Bureau of Standards. The following burn times in seconds are recorded after a paper tab is ignited on the hem of a dress made of each fabric. (a) State the statistica
> Refer to the data on travel expenses and the F-test. It is the ordering of the population means, and the sizes of their differences, that is the key finding of study. (a) Calculate 95% simultaneous confidence intervals for the differences in means. (b)
> Compute the sums of squares and construct the ANOVA table for the data given in Exercise 14.31. Use software to verify your ANOVA table. Data from Exercise 14.31: Food scientists investigated whether making a cheese sauce by a continuous process or bat
> Food scientists investigated whether making a cheese sauce by a continuous process or batch process made any difference to taste. They also included a third treatment, a carefully selected ideal product, that served as a control. Treatment I is the ideal
> A large organization is being investigated to determine if its recruitment is sex-biased. Tables 15 and 16, respectively, show the classification of applicants for secretarial and for sales positions according to gender and result of interview. Table 17
> A random sample of 130 business executives was classified according to age and the degree of risk aversion as measured by a psychological test. Do these data demonstrate an association between risk aversion and age?
> By polling a random sample of 350 undergraduate students, a campus press obtains the following frequency counts regarding student attitude toward a proposed change in dormitory regulations. Are attitude toward the proposal and gender associated?
> Using the data for drugs l and 3 in Exercise 13.33, make a 2 * 2 contingency table and test H0 : p1 = p3 versus H 1 : p1 ≠p3 at a = .05 employing: (a) The x2 test. (b) The Z test. Data from Exercise 13.33: To compare the effectivene
> To compare the effectiveness of four drugs in relieving postoperative pain, an experiment was done by randomly assigning 195 surgical patients to the drugs under study. Recorded here are the number of patients assigned to each drug and the number of pati
> Find the standard deviation of the measurements of diameters given in Exercise 2.45. Data from Exercise 2.45: The following measurements of the diameters (in feet) of Indian mounds in southern Wisconsin were gathered by examining reports in the Wisconsi
> Refer to the data in Exercise 13.31. (a) Use the Z test for testing the equality of two population proportions with a two-sided alternative. Verify the relation x2 = Z2 by comparing their numerical values. (b) If the alternative is that the incidence r
> Refer to Exercise 3.48 and the data concerning a vaccine for type B hepatitis. Do these data indicate that there is a different rate of incidence of hepatitis between the vaccinated and nonvaccinated participants? Use the x2 test for homogeneity in a con
> Referring to the data for site 3 and site 4 in Exercise 13.29, make a 2 * 2 table and test H0 : p3 = p4 versus H1 : p3 > p4 at a = .05. (a) Is there strong evidence that the probability a paper will be taken from the drop site is higher for site 3 th
> A community paper in the Spanish language was delivered to many sites in the San Francisco Bay area. As a check on the circulation numbers that are important to advertisers, a survey was conducted at four drop sites. The number of papers delivered to eac
> The following table records the observed number of births at a hospital in four consecutive quarterly periods. It is conjectured that twice as many babies are born during the Jan.-March quarter than any of the other three quarters. At 
> To examine the quality of a random number generator, frequency counts of the individual integers are recorded from an output of 500 integers. The concept of randomness implies that the integers 0, 1, . . . , 9 are equally likely. Based on the observed fr
> Refer to the physical conditioning data given in Data Bank. Use MINITAB or some other package to fit a regression of the final number of sit-ups on the initial number of sit-ups and the gender of the student.
> Recorded here are the scores x1 and x2 in two midterm examinations, the GPA x3, and the final examination score y for 20 students in a statistics class. (a) Ignoring the data of GPA and the first midterm score, fit a simple linear regression of y on x2.
> A forester seeking information on basic tree dimensions obtains the following measurements of the diameters 4.5 feet above the ground and the heights of 12 sugar maple trees ( courtesy of A. Ek). The forester wishes to determine if the diameter measureme
> Refer to the data of speed x and stopping distance y given in Table I. The MINITAB commands for fitting a straight line regression to y’ = √y and x are (a) Obtain the computer output and identify the equation of the fi
> In 20 17, there were eight skyscrapers in the world over 500 meters tall. The ordered heights are 508 530 541 555 594 601 632 828 (a) Calculate the sample variance for the eight skyscrapers. (b) Calculate the sample standard deviation. (c) Drop the lar
> Listed below are the price quotations on an Internet site for a midsize foreign used car along with their age and odometer mileage. Perform a multiple regression analysis of these data. In particular. (a) Determine the equation for predicting the price f
> Consider the data on male wolves in Table D.9 of the Data Bank concerning age (years) and canine length (mm). (a) Obtain the least squares fit of canine length to the predictor age. (b) Obtain the least squares fit of canine length to a quadratic functi
> An experimenter obtains the following residuals after fitting a quadratic expression in x. Do the basic assumptions appear to be violated?
> The following predicted values and residuals are obtained in an experiment conducted to determine the degree to which the yield of an important chemical in the manufacture of penicillin is dependent on sugar concentration (the time order of the experimen
> A second-degree polynomial y = β^o + β^1x + β^2x2 is fitted to a response y, and the following predicted values and residuals are obtained. Do the assumptions appear to be violated?
> Given the data, (a) Fit a quadratic curve using the equations on page 391. (b) Verify your answers using software.
> The data on the maximum height (feet) and top speed (mph) of the 12 highest roller coasters, displayed in the chapter opener, are (a) Use MINITAB or some other software program to determine the proportion of variation in speed due to regression on height
> Use MINITAB or some other software to obtain the scatter diagram, correlation coefficient, and the regression line of the final time to run 1.5 miles on the initial times given in the Data Bank.
> Use MINITAB or some other software program to regress the marine growth on freshwater growth for the fish growth data of the Data Bank. Do separate regression analyses for: (a) All fish. (b) Males. (c) Females. Your analysis should include (i) a scat
> The least squares fit of polar bear weight to body length is obtained in Example 5. Taking skull length instead of body length, the summary statistics for y = weight and x = skull length, based on Table D.13 of the Data Bank, are (a) Obtain the equation
> For each data set, calculate s2. (a) 1 4 3 2 2 (b) -2 1 -1 - 3 0 -2 (c) 9 8 8 9 8 8 9
> Refer to Exercise 11.56 and a least squares fit using the data on all of the wolves in Table D.9 of the Data Bank concerning body length (cm) and weight (lb). There is one obvious outlier, row 18 with body length 123 and weight 106. Drop this observation
> Consider the data on all of the wolves in the Data Bank concerning body length ( cm) and weight (lb). Using MINITAB or some other software program: (a) Plot weight versus body length. (b) Obtain the least squares fit of weight to the predictor variable
> Consider the data on wolves in the Data Bank concerning body length (cm) and weight (lb). Calculate the correlation coefficient r and r2 for (a) All wolves. (b) Male wolves. (c) Female wolves. (d) Comment on the differences in your answers. Make a mu
> The calculations involved in a regression analysis become increasingly tedious with larger data sets. Access to a computer proves to be of considerable advantage. We repeat here a computer based analysis of linear regression using the data of Example 4 a
> Again referring to Exercise 11.51, find the sample correlation coefficient between age and selling price. What proportion of the variability in price is explained by the fitted straight line? Comment on the adequacy of the straight line fit. Data from E
> Refer to Exercise 11.51. (a) From the fitted regression line, determine the predicted value for the average selling price of a 5-year-old car and construct a 95% confidence interval. (b) Determine the predicted value for a 5-year-old car to be listed o
> A top Internet site features used cars for sale. The age, x, measured in years and the price, y, expressed in thousands of dollars were recorded from a sample of listings for a popular midsize foreign car. (a) Plot the scatter diagram. (b) Determine the
> Refer to Exercise 11.49. (a) Calculate the sample correlation coefficient. (b) What proportion of the y variability is explained by the fitted regression line? Data from Exercise 11.49: A recent graduate moving to a new job collected a sample of month
> A recent graduate moving to a new job collected a sample of monthly rent ( dollars) and size (square feet) of 2-bedroom apartments in one area of a Midwest city. (a) Plot the scatter diagram and find the least squares fit of a straight line. (b) Do thes
> Refer to Exercise 11.47. (a) Obtain the decomposition of the total y variability into two parts: one explained by linear relation and one not explained . (b) What proportion of the y variability is explained by the straight line regression? (c) Calcul
> A sample of six university students responded to the question "H ow much time, in minutes, did you spend on the social network site yesterday?" One student never used the site and was dropped from the study. 100 45 60 130 30 Calculate, using these five v
> Many college students obtain college degree credits by demonstrating their proficiency on exams developed as part of the College Level Examination Program (CLEP). Based on their scores on the College Qualification Test (CQT), it is helpful if students co
> Refer to Exercise 11.44. (a) Construct a 95% confidence interval for the slope of the regression line. (b) Obtain a 90% confidence interval for the expected y value corresponding to x = 4 days. Data from Exercise 11.44: Last week's total number of hou
> Refer to Exercise 11.44. (a) Find the residuals. (b) Calculate the SSE by (i) summing the squares of the residuals and also (ii) using the formula SSE = Syy – S2xy / Sxx. (c) Estimate the error variance. Data from Exercise 11.44: Las
> Last week's total number of hours worked by a student, y, depends on the number of days, x, he reported to work last week. Suppose the data from nine students provided (a) Plot the scatter diagram. (b) Calculate x, y, Sxx, Syy , and Sxy. (c) Determine t
> Concerns that were raised for the environment near a government facility led to a study of plants. Since leaf area is difficult to measure, the leaf area ( cm2 ) was fit to x = Leaf length * Leaf width using a least squares approach. For data collected
> Students can bike to a park on the other side of a lake by going around one side of the lake or the other. After much discussion about which was faster, they decided to perform an experiment. Among the 12 students available, 6 were randomly selected to f
> Two scales are available at a campus athletic facility. A student wonders if, on average, they give the same reading for weight. She and four others weigh themselves on both scales. The readings are (a) Find a 95% confidence interval for the mean differe
> A sample of river water is divided into two specimens. One is randomly selected to be sent to Lab A and the other is sent to Lab B. This is repeated for a total of nine times. The measurement of suspended solids at Lab B is subtracted from that of Lab A
> A driver is stopped for erratic driving, and the alcohol content of his blood is checked. Specify the sample space and the event A = [ level exceeds legal limit ] if the legal limit is .10%.
> Examine each of these probability assignments and state what makes it improper. (a) Concerning tomorrow's weather, P( Rain) = .4 P ( Cloudy but no rain) = . 5 P( Sunny) = .2 (b) Concerning your passing of the statistics course, P( Pass) = 1.1 P( Fa
> For the data of Exercise 2.57, calculate s2 by using the alternative formula. Data from Exercise 2.57: For the data set 6 2 4
> Identify these events in the corresponding parts of Exercise 4.95. (a) At most 7 commercials. (b) Less than 18 .5 hours. (c) At least 30% visited a site. Data from Exercise 4.95: Describe the sample space for each of the following experiments. (a) T
> In order to keep up with the demand for its new earphones, a manufacturer h ad to purchase a key p art from three different suppliers. Supplier l provides 15% of the parts and 10% are defective. Supplier 2 provides 60% of the parts and 4% are defective.
> Identity theft is a growing problem in the United States. According to a Federal Trade Commission Report about 280,000 identity complaints were filed in a recent year. Among the 43.2 million persons in the 20- 29 year old age group, 56,689 complaints wer
> An e-commerce electronics firm sent 80% of its orders by a parcel service that delivers late only 3% of the time. It sends the other 20% of items by a combination bus service and local transportation that delivers late 6% of the time. Find the (a) The p

