Question: The responses of 1254 voters to a
The responses of 1254 voters to a survey about the way the media conducted themselves in the 2016 presidential campaign are shown in the Pareto chart. Find the probability of each event.
a. Randomly selecting a person from the sample who did not give the media an A or a B
b. Randomly selecting a person from the sample who gave the media a grade better than a D
c. Randomly selecting a person from the sample who gave the media a D or an F
d. Randomly selecting a person from the sample who gave the media a C or a D
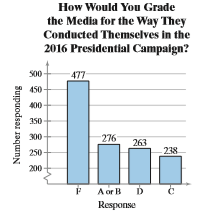
Transcribed Image Text:
How Would You Grade the Media for the Way They Conducted Themselves in the 2016 Presidential Campalgn? S00 477 450 400 350 300 276 263 250 238 200 A or B D Response Number responding
> The age distribution of the residents of Kadoka, South Dakota, is shown at the left. Find the probability of the event. Event D: randomly choosing a resident who is not 75 years old or older Ages Frequency, f 0-14 173 15-29 123 30-44 92 45-59 137 60
> The age distribution of the residents of Kadoka, South Dakota, is shown at the left. Find the probability of the event. Event C: randomly choosing a resident who is not 14 years old or younger Ages Frequency, f 0-14 173 15-29 123 30-44 92 45-59 137
> The age distribution of the residents of Kadoka, South Dakota, is shown at the left. Find the probability of the event. Event B: randomly choosing a resident who is not 45 to 59 years old Ages Frequency, f 0-14 173 15-29 123 30-44 92 45-59 137 60-74
> Determine whether the statement is true or false. If it is false, explain why. If events A and B are mutually exclusive, then P(A or B)= P(A)+ P(B).
> The age distribution of the residents of Kadoka, South Dakota, is shown at the left. Find the probability of the event. Event A: randomly choosing a resident who is not 15 to 29 years old Ages Frequency, f 0-14 173 15-29 123 30-44 92 45-59 137 60-74
> Classify the statement as an example of classical probability, empirical probability, or subjective probability. Explain your reasoning. You think that a football team’s probability of winning its next game is about 0.80.
> Classify the statement as an example of classical probability, empirical probability, or subjective probability. Explain your reasoning. The probability that a randomly selected number from 1 to 100 is divisible by 6 is 0.16.
> Give three observations that can be made from the graph. Amount Spent on Pet Care 10 Туре of care Amount spent (in billions) pon SuppliesOTC medicine Veterinarian care Supaog sogund
> Classify the statement as an example of classical probability, empirical probability, or subjective probability. Explain your reasoning. According to a survey, the probability that an adult chosen at random is in favor of a sprinkling ban is about 0.45.
> Classify the statement as an example of classical probability, empirical probability, or subjective probability. Explain your reasoning. An analyst feels that a certain stock’s probability of decreasing in price over the next week is 0.75.
> Classify the statement as an example of classical probability, empirical probability, or subjective probability. Explain your reasoning. The probability of choosing 6 numbers from 1 to 40 that match the 6 numbers drawn by a state lottery is 1/3,838,380 ≈
> Classify the statement as an example of classical probability, empirical probability, or subjective probability. Explain your reasoning. According to company records, the probability that a washing machine will need repairs during a six-year period is 0.
> Use the frequency distribution at the left, which shows the number of voting-age American citizens (in millions) by age, to find the probability that a citizen chosen at random is in the age range. 65 years old and older Frequency, f (in millions) A
> Use the frequency distribution at the left, which shows the number of voting-age American citizens (in millions) by age, to find the probability that a citizen chosen at random is in the age range. 45 to 64 years old Frequency, f (in millions) Ages
> Use the frequency distribution at the left, which shows the number of voting-age American citizens (in millions) by age, to find the probability that a citizen chosen at random is in the age range. 30 to 44 years old Frequency, f (in millions) Ages
> Determine whether the statement is true or false. If it is false, explain why. The probability that event A or event B will occur is P(A or B)= P(A)+ P(B) + P(A and B)
> Use the frequency distribution at the left, which shows the number of voting-age American citizens (in millions) by age, to find the probability that a citizen chosen at random is in the age range. 18 to 29 years old Frequency, f (in millions) Ages
> A polling organization is asking a sample of U.S. adults how many tattoos they have. The frequency distribution at the left shows the results. Use the frequency distribution. /’ What is the probability that the next person asked has two tattoos?
> Give three observations that can be made from the graph. Least Popular American Drivers The Multitasker 8% - The Swerver 8% The Crawler 8% The Speeder 5% The Left-Lane Hog 11% - The Drifter 5% Other 6% -The Texter The Last-Minute Line-Cutter 13% 22%
> A polling organization is asking a sample of U.S. adults how many tattoos they have. The frequency distribution at the left shows the results. Use the frequency distribution. /’ What is the probability that the next person asked does not have a tattoo?
> A probability experiment consists of rolling a 12-sided die, numbered 1 to 12. Find the probability of the event. Event F: rolling a number divisible by 5
> A probability experiment consists of rolling a 12-sided die, numbered 1 to 12. Find the probability of the event. Event E: rolling a number divisible by 3
> A probability experiment consists of rolling a 12-sided die, numbered 1 to 12. Find the probability of the event. Event D: rolling a number less than 8
> A probability experiment consists of rolling a 12-sided die, numbered 1 to 12. Find the probability of the event. Event C: rolling a number greater than 4
> • The probability that an airplane flight departs on time is 0.89. • The probability that a flight arrives on time is 0.87. • The probability that a flight departs and arrives on time is 0.83. Find the probability that a flight arrives on time given th
> • The probability that an airplane flight departs on time is 0.89. • The probability that a flight arrives on time is 0.87. • The probability that a flight departs and arrives on time is 0.83. Find the probability that a flight departed on time given t
> You are in a class that has 24 students. You want to find the probability that at least two of the students have the same birthday. a. Find the probability that each student has a different birthday. b. Use the result of part (a) to find the probabilit
> Determine whether the statement is true or false. If it is false, explain why. When two events are independent, they are also mutually exclusive.
> A virus infects one in every 200 people. A test used to detect the virus in a person is positive 80% of the time when the person has the virus and 5% of the time when the person does not have the virus. (This 5% result is called a false positive.) Let A
> Give three observations that can be made from the graph. Motor Vehicle Thefts at U.S. Universities and Colleges 1900 1880- 1800 1750 1700 1650 1600 2010 2011 2012 2013 2014 2015 Year Thefts
> Use Bayes’ Theorem to find P(A|B). P(A)= 12%, P(A′)= 88%, P(B|A)= 66%, and P(B|A′)= 19%
> Use Bayes’ Theorem to find P(A|B). P(A)= 73%, P(A′)= 17%, P(B|A)= 46%, and P(B|A′)= 52%
> Use Bayes’ Theorem to find P(A|B). P(A)= 0.62, P(A′)= 0.38, P(B|A)= 0.41, and P(B|A′)= 0.17
> Use Bayes’ Theorem to find P(A|B). P(A)= 0.25, P(A′)= 0.75, P(B|A)= 0.3, and P(B|A′)= 0.5
> Use Bayes’ Theorem to find P(A|B). P(A)= 3/8, P(A′)= 5/8, P(B|A)= 2/3, and P(B|A′)= 3/5
> Use Bayes’ Theorem to find P(A|B). P(A)= 2/3, P(A′)= 1/3, P(B|A)= 1/5, and P(B|A′)= 1/2
> Use the Multiplication Rule. A doctor gives a patient a 60% chance of surviving bypass surgery after a heart attack. If the patient survives the surgery, then the patient has a 50% chance that the heart heals. Find the probability that the patient surviv
> Use the Multiplication Rule. According to a study, 80% of K–12 schools or districts in the United States use digital content such as ebooks, audio books, and digital textbooks. Of these 80%, 4 out of 10 use digital content as part of their curriculum. Fi
> Can two events with nonzero probabilities be both independent and mutually exclusive? Explain your reasoning.
> Determine whether the statement is true or false. If it is false, explain why. When two events are mutually exclusive, they have no outcomes in common.
> Give three observations that can be made from the graph. Monthly Active Users on 5 Social Networking Sites as of September 2016 1750 1500 1250 1000 750 500 250 Site Number of users (in millions) Instagram Twitter Pinterest
> Explain, in your own words, why in the Addition Rule for P(A or B or C), P(A and B and C) is added at the end of the formula.
> In the Venn diagram, P(A or B or C) is represented by the blue areas. Find P(A or B or C). P(A)= 0.38, P(B)= 0.26, P(C)= 0.14, P(A and B)= 0.12, P(A and C)= 0.03, P(B and C)= 0.09, P(A and B and C)= 0.01 B
> In the Venn diagram, P(A or B or C) is represented by the blue areas. Find P(A or B or C). P(A)= 0.40, P(B)= 0.10, P(C)= 0.50, P(A and B)= 0.05, P(A and C)= 0.25, P(B and C)= 0.10, P(A and B and C)= 0.03 B
> The table shows the results of a survey that asked 3203 people whether they wore contacts or glasses. A person is selected at random from the sample. Find the probability of each event. a. The person wears only contacts or only glasses. b. The person i
> The table shows the results of a survey that asked 2850 people whether they were involved in any type of charity work. A person is selected at random from the sample. Find the probability of each event. a. The person is male or frequently involved in ch
> The table shows the results of a survey that asked 506 Maine adults whether they favored or opposed a tax to fund education. A person is selected at random from the sample. Find the probability of each event. a. The person oppose
> The table shows the numbers of male and female students in the U.S. who received bachelor’s degrees in business in a recent year. A student is selected at random. Find the probability of each event. a. The student is male or received
> The responses of 1007 American adults to a survey question about the story of Britons’ vote to leave the European Union are shown in the Pareto chart. Find the probability of each event. a. Randomly selecting an adult who thinks the st
> The percent of college students’ marijuana use for a sample of 95,761 students is shown in the pie chart. Find the probability of each event. a. Randomly selecting a student who never used marijuana b. Randomly selecting a student who
> Use the stem-and-leaf plot or dot plot to list the actual data entries. What is the maximum data entry? What is the minimum data entry? .... 215 220 225 230 215
> Use the frequency histogram to a. determine the number of classes. b. estimate the greatest and least frequencies. c. determine the class width. d. describe any patterns with the data. Employee Salaries 300- 250 200 150 100 50- Salary (in thousan
> Give an example of a. two events that are mutually exclusive and b. two events that are not mutually exclusive.
> The estimated percent distribution of the U.S. population for 2025 is shown in the pie chart. Find the probability of each event. a. Randomly selecting someone who is under 5 years old b. Randomly selecting someone who is 45 years or over c. Randomly s
> You roll a die. Find the probability of each event. a. Rolling a 5 or a number greater than 3 b. Rolling a 2 or an odd number c. Rolling a number less than 4 or an even number
> A card is selected at random from a standard deck of 52 playing cards. Find the probability of each event. a. Randomly selecting a club or a 3 b. Randomly selecting a red suit or a king c. Randomly selecting a 9 or a face card
> Of the cans produced by a company, 96% do not have a puncture, 93% do not have a smashed edge, and 89.3% do not have a puncture and do not have a smashed edge. Find the probability that a randomly selected can does not have a puncture or a smashed edge.
> Of the cartons produced by a company, 5% have a puncture, 8% have a smashed corner, and 0.4% have both a puncture and a smashed corner. Find the probability that a randomly selected carton has a puncture or a smashed corner.
> A teaching conference has an attendance of 6855 people. Of these, 3120 are college professors and 3595 are male. Of the college professors, 1505 are male. Find the probability that a randomly selected attendee is male or a college professor.
> A physics class has 40 students. Of these, 12 students are physics majors and 16 students are female. Of the physics majors, three are female. Find the probability that a randomly selected student is female or a physics major.
> Determine whether the events are mutually exclusive. Explain your reasoning. Event A: Randomly select a member of the U.S. Congress. Event B: Randomly select a male U.S. Senator.
> Determine whether the events are mutually exclusive. Explain your reasoning. Event A: Randomly select a voter who is a registered Republican. Event B: Randomly select a voter who is a registered Democrat.
> Use the stem-and-leaf plot or dot plot to list the actual data entries. What is the maximum data entry? What is the minimum data entry? 13 14 15 16 17 18 19
> Determine whether the events are mutually exclusive. Explain your reasoning. Event A: Randomly select a student with a birthday in April. Event B: Randomly select a student with a birthday in May.
> When two events are mutually exclusive, why is P(A and B)= 0?
> Determine whether the events are independent or dependent. Explain your reasoning. Selecting a king from a standard deck of 52 playing cards, replacing it, and then selecting a queen from the deck
> Use the table to find each conditional probability. The table shows the results of a survey in which 250Â male and 250 female workers ages 25 to 64 were asked if they contribute to a retirement savings plan at work. a. Find the probability th
> Use the table to find each conditional probability. The table shows the numbers of male and female students in the United States who received bachelor’s degrees in business in a recent year. a. Find the probability that a randomly sele
> Determine whether the statement is true or false. If it is false, rewrite it as a true statement. If events A and B are dependent, then P(A and B)= P(A)·P(B).
> Determine whether the statement is true or false. If it is false, rewrite it as a true statement. If two events are independent, then P(A|B)= P(B).
> Explain how to use the complement to find the probability of getting at least one item of a particular type.
> Use the Multiplication Rule. According to a survey, 49% of U.S. adults have purchased a state lottery ticket in the past 12 months. Of these 49%, about 27.5% have annual incomes less than $36,000. a. Find the probability that a randomly selected U.S. ad
> What does the notation P(B|A) mean?
> Use the stem-and-leaf plot or dot plot to list the actual data entries. What is the maximum data entry? What is the minimum data entry? 12 Key: 12|9 = 12.9 12 9 13 3 13 677 14 11113 4 4 14 699 15 000124 15 67 888 9 16 1 16 67
> Use the Multiplication Rule. In a recent year, about 1.6% of all infants born in the U.S. were conceived through in vitro fertilization (IVF). Of the IVF deliveries, about 41.1% resulted in multiple births. a. Find the probability that a randomly select
> Use the Multiplication Rule. The probability that a Caucasian person in the United States has type AB- blood is 1%. Four unrelated Caucasian people in the United States are selected at random. a. Find the probability that all four have type AB- blood.
> Use the Multiplication Rule. The probability that an African American person in the United States has type O+ blood is 47%. Six unrelated African American people in the United States are selected at random. a. Find the probability that all six have type
> Use the Multiplication Rule. In a sample of 1446 U.S. registered voters, 188 said that Richard Nixon was the worst president since World War II. Three registered voters are selected at random without replacement. a. Find the probability that all three r
> Use the Multiplication Rule. In a sample of 1446 U.S. registered voters, 217 said that John Kennedy was the best president since World War II. Two registered voters are selected at random without replacement. a. Find the probability that both registered
> Use the Multiplication Rule. In a sample of 1000 U.S. adults, 300 said they know a murder victim. Four U.S. adults are selected at random without replacement. a. Find the probability that all four adults know a murder victim. b. Find the probability tha
> Use the Multiplication Rule. In a sample of 1000 U.S. adults, 200 think that most Hollywood celebrities are good role models. Two U.S. adults are selected at random without replacement. a. Find the probability that both adults think that most Hollywood c
> Use the Multiplication Rule. In a survey, 510 U.S. adults were asked whether they drive a pickup truck and whether they drive a Ford. The results showed that three in ten adults surveyed drive a Ford. Of the adults surveyed that drive Fords, two in nine
> Use the Multiplication Rule. Research has shown that approximately 1 woman in 600Â carries a mutation of the BRCA1 gene. About 60% of women with this mutation develop breast cancer. Find the probability that a randomly selected woman will carr
> Use the Multiplication Rule. A coin is tossed and a die is rolled. Find the probability of tossing a tail and then rolling a number greater than 2.
> Name some ways to display quantitative data graphically. Name some ways to display qualitative data graphically.
> Give an example of a. two events that are independent. b. two events that are dependent.
> Use the Multiplication Rule. Two cards are selected from a standard deck of 52 playing cards. The first card is not replaced before the second card is selected. Find the probability of selecting a heart and then selecting a club.
> Identify the two events described in the study. Do the results indicate that the events are independent or dependent? Explain your reasoning. According to researchers, high engagement with mobile technology for escapism is linked to depression and anxiet
> Identify the two events described in the study. Do the results indicate that the events are independent or dependent? Explain your reasoning. A study found that there is no relationship between playing violent video games and aggressive or bullying behav
> Identify the two events described in the study. Do the results indicate that the events are independent or dependent? Explain your reasoning. Certain components in coffee have been found to cause the body to produce higher amounts of acid, which can irri
> Identify the two events described in the study. Do the results indicate that the events are independent or dependent? Explain your reasoning. A study found that people who suffer from obstructive sleep apnea are at increased risk of having heart disease.
> Determine whether the events are independent or dependent. Explain your reasoning. A ball is selected from a bin of balls numbered from 1 through 52. It is replaced, and then a second numbered ball is selected from the bin.
> Determine whether the events are independent or dependent. Explain your reasoning. Rolling a six-sided die and then rolling the die a second time so that the sum of the two rolls is five
> Determine whether the events are independent or dependent. Explain your reasoning. Not putting money in a parking meter and getting a parking ticket
> Determine whether the events are independent or dependent. Explain your reasoning. Returning a rented movie after the due date and receiving a late fee
> Determine whether the statement is true or false. If it is false, rewrite it as a true statement. An ogive is a graph that displays relative frequencies.
> Determine whether the events are independent or dependent. Explain your reasoning. A father having hazel eyes and a daughter having hazel eyes
> What is the difference between independent and dependent events?
> Determine whether the statement is true or false. If it is false, rewrite it as a true statement. A probability of 1/10 indicates an unusual event.
> Determine whether the statement is true or false. If it is false, rewrite it as a true statement. You toss a fair coin nine times and it lands tails up each time. The probability it will land heads up on the tenth toss is greater than 0.5.

