[SOLVED] There is a tie for the choice

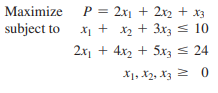
> Use the big M method to solve the Problem.

> Find the transpose of each matrix.

> Use formula (1) for simple interest to find each of the indicated quantities. P = $950; r = 9%; t = 1 year; I = ?

> Repeat Problem 57 if the weekly cost of busing a student from North Division to Washington is $7 and all other data remain the same. Data From Problem 57: A metropolitan school district has two overcrowded high schools and two underenrolled high schools

> A farmer can buy three types of plant food: mix A, mix B, and mix C. Each cubic yard of mix A contains 20 pounds of phosphoric acid, 10 pounds of nitrogen, and 10 pounds of potash. Each cubic yard of mix B contains 10 pounds of phosphoric acid, 10 pounds

> Repeat Problem 50 if it costs $800 per hour to operate the West Summit mine and $200 per hour to operate the North Ridge mine and all other data remain the same. Data from Problem 50: A mining company operates two mines, each producing three grades of o

> Repeat Problem 50 if it costs $300 per hour to operate the West Summit mine and $700 per hour to operate the North Ridge mine and all other data remain the same. Data from Problem 50: A mining company operates two mines, each producing three grades of o

> A mining company operates two mines, each producing three grades of ore. The West Summit mine can produce 2 tons of low-grade ore, 3 tons of medium-grade ore, and 1 ton of high-grade ore in one hour of operation. The North Ridge mine can produce 2 tons o

> Solve the linear programming problems by applying the simplex method to the dual problem. Repeat Problem 47 with C = 4x1 + 7x2 + 5x3 + 6x4 Data from Problem 47:

> Solve the linear programming problems by applying the simplex method to the dual problem.

> (A) Form an equivalent minimization problem with Ã problem constraints (multiply inequalities by -1 if necessary), (B) Form the dual of the equivalent problem. (C) Is the dual problem a standard maximization problem in standard form? Expla

> (A) Form the dual problem. (B) Is the dual problem a standard maximization problem in standard form? Explain

> If you want to solve a minimization problem by applying the geometric method to the original problem, how many variables and problem constraints must be in the original problem?

> Use the given annual interest rate r and the compounding period to find i, the interest rate per compounding period. 2.94% compounded semiannually

> A minimization problem has 3 variables and 5 problem constraints. How many variables and problem constraints are in the dual problem?

> Solve the linear programming problems by applying the simplex method to the dual problem.

> (A) Form the dual problem. (B) Find the solution to the original problem by applying the simplex method to the dual problem.

> Convert the given time period to years, in reduced fraction form, assuming a 360-day year [this assumption does not affect the number of quarters (4), months (12), or weeks (52) in a year]. 7 Quarters

> (A) Form the dual problem. (B) Find the solution to the original problem by applying the simplex method to the dual problem.

> a minimization problem, the corresponding dual problem, and the final simplex tableau in the solution of the dual problem are given. (A) Find the optimal solution of the dual problem. (B) Find the optimal solution of the minimization problem.

> (A) Form the dual problem. (B) Write the initial system for the dual problem. (C) Write the initial simplex tableau for the dual problem and label the columns of the tableau.

> Find the transpose of each matrix.

> (A) Using slack variables, write the initial system for each linear programming problem. (B) Write the simplex tableau, circle the first pivot, and identify the entering and exiting variables. (C) Use the simplex method to solve the problem Repeat Prob

> (A) Using slack variables, write the initial system for each linear programming problem. (B) Write the simplex tableau, circle the first pivot, and identify the entering and exiting variables. (C) Use the simplex method to solve the problem

> find the pivot element, identify the entering and exiting variables, and perform one pivot operation.

> Use the given annual interest rate r and the compounding period to find i, the interest rate per compounding period. 3.84% compounded monthly

> For the simplex tableaux. (A) Identify the basic and nonbasic variables. (B) Find the corresponding basic feasible solution. (C) Determine whether the optimal solution has been found, an additional pivot is required, or the problem has no optimal solut

> Repeat Problem 55 if one of the requirements of the grant is that at least 50% of the interviewers be undergraduate students. Data from Problem 55: A political scientist received a grant to fund a research project on voting trends. The budget includes $

> Repeat Problem 53 if the scientist wants to maximize the daily calcium intake while not allowing the intake of iron or protein to exceed the average daily intake. Data from Problem 53: The natural diet of a certain animal consists of three foods: A, B,

> Repeat Problem 48 if the profit on a five-speed bicycle increases from $70 to $110 and all other data remain the same. If the slack associated with any problem constraint is nonzero, find it. Data from problem 48: A company manufactures three speed, fiv

> Repeat Problem 48 if the profit on a ten-speed bicycle increases from $100 to $110 and all other data remain the same. If the slack associated with any problem constraint is nonzero, find it. Data from problem 48: A company manufactures three speed, fiv

> A company manufactures three speed, five-speed, and ten-speed bicycles. Each bicycle passes through three departments: fabrication, painting & plating, and final assembly. The relevant manufacturing data are given in the table. How many bicycles of

> Repeat Problem 45 if the department store increases its budget to $24,000 and requires that at least half of the ads be placed during prime-time. Data from Problem 45: A department store has up to $20,000 to spend on television advertising for a sale. A

> Repeat Problem 43 under the additional assumption that no more than $30,000 can be invested in money market funds. Data from Problem 43: An investor has at most $100,000 to invest in government bonds, mutual funds, and money market funds. The average yi

> Solve Problem 41 with the additional restriction that the combined total number of components produced each week cannot exceed 420. Discuss the effect of this restriction on the solution to Problem 41. Data from Problem 41: A small company manufactures

> Convert the given time period to years, in reduced fraction form, assuming a 360-day year [this assumption does not affect the number of quarters (4), months (12), or weeks (52) in a year]. 6 Weeks

> There is a tie for the choice of the first pivot column. Use the simplex method to solve each problem two different ways: first by choosing column 1 as the first pivot column, and then by choosing column 2 as the first pivot column. Discuss the relations

> Solve by the simplex method and also by graphing (the geometric method). Compare and contrast the results.

> first solve the linear programming problem by the simplex method, keeping track of the basic feasible solutions at each step. Then graph the feasible region and illustrate the path to the optimal solution determined by the simplex method.

> Solve the linear programming problems using theÂ simplex method.

> Solve the linear programming problems using theÂ simplex method. Repeat Problem 29 with P = 20x1 + 20x2. Data from Problem 29

> Solve the linear programming problems using theÂ simplex method.

> Use the continuous compound interest formula (3) to find each of the indicated values A = $23,600; P = $19,150; t = 60 months; r = ?

> Evaluate the expression. If the answer is not an integer, round to four decimal places. 10P7

> Solve the linear programming problems using theÂ simplex method.

> Solve the linear programming problems using theÂ simplex method. Repeat Problem 17 with P = x1 + 2x2. Data from Problem 17:

> Solve the linear programming problems using theÂ simplex method.

> Evaluate the expression. In how many ways can three variables be chosen from x1, x2, s1, s2, s3, s4, s5, s6, and assigned the value 0?

> Evaluate the expression. In how many ways can three variables be chosen from x1, x2, x3, s1, s2, s3 and assigned the value 0?

> Evaluate the expression.

> A linear programming problem has 40 decision variables x1, x2, c , x40 and 85 problem constraints. How many rows are there in the table of basic solutions of the associated e-system? (Write the answer using scientific notation.)

> A linear programming problem has five decision variables x1, x2, x3, x4, x5 and six problem constraints. How many rows are there in the table of basic solutions of the associated e-system?

> Convert the given time period to years, in reduced fraction form, assuming a 360-day year [this assumption does not affect the number of quarters (4), months (12), or weeks (52) in a year]. 90 Days

> Explain why the linear programming problem has an optimal solution, and find it using the table method.

> Explain why the linear programming problem has no optimal solution.

> Solve the given linear programming problem using the table method.

> If a1x1 + a2x2 ≤ b is one of the problem constraints in a standard maximization problem in standard form with two decision variables, and a1 and a2 are both positive, explain why the optimal value of the objective function exists.

> For a standard maximization problem in standard form, with k decision variables, x1, x2,. . xk, explain why the feasible region is not empty.

> Graph the system of inequalities from the given problem, and list the corner points of the feasible region. Verify that the corner points of the feasible region correspond to the basic feasible solutions of the associated e-system Problem 46.

> Use the continuous compound interest formula (3) to find each of the indicated values A = $32,982; P = $27,200; r = 5.93%; t = ?

> Graph the system of inequalities from the given problem, and list the corner points of the feasible region. Verify that the corner points of the feasible region correspond to the basic feasible solutions of the associated e-system Problem 44.

> Graph the system of inequalities from the given problem, and list the corner points of the feasible region. Verify that the corner points of the feasible region correspond to the basic feasible solutions of the associated e-system Problem 42.

> Convert the given i-system to an e-system using slack variables. Then construct a table of all basic solutions of the e-system. For each basic solution, indicate whether or not it is feasible.

> Refer to the partially completed table below of the 10 basic solutions to the e-system Find basic solution (J).

> Refer to the partially completed table below of the 10 basic solutions to the e-system Find basic solution (H).

> Refer to the partially completed table below of the 10 basic solutions to the e-system Which of the basic solutions (A) through (F) are feasible? Explain.

> Refer to the partially completed table below of the 10 basic solutions to the e-system In basic solution (I), which variables are basic?

> Convert the given time period to years, in reduced fraction form, assuming a 360-day year [this assumption does not affect the number of quarters (4), months (12), or weeks (52) in a year]. 9 Months

> Refer to the partially completed table below of the 10 basic solutions to the e-system In basic solution (E), which variables are nonbasic?

> Refer to the table below of the six basic solutions to the e-system Describe geometrically the set of all points in the plane such that s2

> Refer to the table below of the six basic solutions to the e-system Use the basic feasible solutions to maximize P = 8x1 + 5x2.

> Refer to the table below of the six basic solutions to the e-system Which of the basic solutions are not feasible? Explain.

> Refer to the table below of the six basic solutions to the e-system In basic solution (D), which variables are basic?

> Refer to the table below of the six basic solutions to the e-system In basic solution (B), which variables are nonbasic?

> write the e-system obtained via slack variables for the given linear programming problem.

Question: There is a tie for the choice