[SOLVED] use a graphing calculator to approximate the

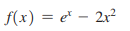
> use the given sign chart to sketch a possible graph of ï¦.

> Find the intervals on which the graph of ï¦ is concave upward, the intervals on which the graph of ï¦ is concave downward, and the x, y coordinates of the inflection points.

> find the x and y coordinates of all inflection points.

> Find the probability of being dealt the given hand from a standard 52-card deck. Refer to the description of a standard 52-card deck on page 384. A 6-card hand that contains exactly two clubs.

> find the x and y coordinates of all inflection points.

> find the indicated derivative for each function.

> match the indicated conditions with one of the graphs (A)â(D) shown in the figure.

> Use the graph of y = (x) to identify (A) The local extrema of (x). (B) The inflection points of (x). (C) The numbers u for which ′(u)is a local extremum of ′(x).

> ï¦(x) is continuous on 1 - â, â2 and has critical numbers at x = a, b, c, and d. Use the sign chart for ï¦â² (x) to determine whether f has a local maximum, a local

> Refer to the following graph of y = ï¦(x): Identify the x coordinates of the points where ï¦(x has a local minimum.

> Refer to Problem 79. If a university student is selected at random, what is the (empirical) probability that (A) The student does not own a car? (B) The student owns a car but not a laptop. Data from problem 79: From a survey involving 1,000 university

> Refer to the Venn diagram below for events A and B in an equally likely sample space S. Find each of the indicated probabilities.

> Refer to the following graph of y = ï¦(x): Identify the x coordinates of the points where ï¦â²(x) does not exist.

> Refer to the following graph of y = ï¦(x): Identify the intervals on which ï¦â² (x) > 0.

> Refer to the following graph of y = ï¦(x): Identify the intervals on which f1x2 is decreasing

> inspect the graph of the function to determine whether it is increasing or decreasing on the given interval.

> The concentration C(t), in milligrams per cubic centimeter, of a particular drug in a patientâs bloodstream is given by where t is the number of hours after the drug is taken orally. Find the critical numbers of C(t), the intervals on

> A manufacturer incurs the following costs in producing x rain jackets in one day for 0 6 x 6 200: fixed costs, $450; unit production cost, $30 per jacket; equipment maintenance and repairs, 0.08x2 dollars. (A) What is the average cost C(x) per jacket if

> The figure approximates the rate of change of the price of eggs over a 70-month period, where E1t2 is the price of a dozen eggs (in dollars) and t is time (in months). (A) Write a brief description of the graph of y = E(t), including a discussion of any

> Find the probability of being dealt the given hand from a standard 52-card deck. Refer to the description of a standard 52-card deck on page 384. A 5-card hand that consists entirely of face cards.

> The graph of the total revenue R(x) (in dollars) from the sale of x cordless electric screwdrivers is shown in the figure. (A) Write a brief description of the graph of the marginal revenue function y = Râ²(x), including a discussion o

> Find the critical numbers, the intervals on which ï¦(x) is increasing, the intervals on which ï¦(x) is decreasing, and the local extrema. Do not graph

> use the given graph of y = ï¦(x) to find the intervals on which ï¦â²(x) > 0, the intervals on which ï¦â²(x) 6 0, and the values of x for which ï¦

> use the given graph of y = ï¦â²(x) to find the intervals on which ï¦ is increasing, the intervals on which ï¦ is decreasing, and the x coordinates of the local extrema of ï

> involve functions ï¦1-ï¦6 and their derivatives, g1-g6. Use the graphs shown in figures (A) and (B) to match each function fi with its derivative gj . ï¦ï¶

> Consider the command in Figure A and the associated statistical plot in Figure B. (A) Explain why the command does not simulate 50 repetitions of rolling a pair of dice and recording their sum. (B) Describe an experiment that is simulated by this comma

> involve functions ï¦1-ï¦6 and their derivatives, g1-g6. Use the graphs shown in figures (A) and (B) to match each function fi with its derivative gj . ï¦ï´

> involve functions ï¦1-ï¦6 and their derivatives, g1-g6. Use the graphs shown in figures (A) and (B) to match each function fi with its derivative gj . ï¦ï²

> ï¦(x) is continuous on (-â, â). Use the given information to sketch the graph of ï¦.

> use a graphing calculator to approximate the critical numbers of ï¦(x) to two decimal places. Find the intervals on which ï¦(x) is increasing, the intervals on which ï¦(x) is decreasing, and the loc

> Find the intervals on which ï¦(x) is increasing and the intervals on which ï¦(x) is decreasing. Then sketch the graph. Add horizontal tangent lines.

> An experiment consists of rolling two fair (not weighted) 4-sided dice and adding the dots on the two sides facing up. Each die is numbered 1–4. Compute the probability of obtaining the indicated sums. An even sum.

> Find the intervals on which ï¦(x) is increasing and the intervals on which ï¦(x) is decreasing. Then sketch the graph. Add horizontal tangent lines.

> Find the intervals on which ï¦(x) is increasing, the intervals on which ï¦(x) is decreasing, and the local extrema.

> Solve the equation P (E) /P (E’) = a/b for P (E). If P (E) = c/d, show that odds in favor of E occurring are c to d – c.

> Find (A) ï¦â²(x), (B) the partition numbers for ï¦â², and (C) the critical numbers of ï¦ .

> Give the local extrema of f and match the graph of ï¦ with one of the sign charts aâh.

> Find the relative rate of change of ï¦(x).

> Use the given equation, which expresses price p as a function of demand x, to find a function ï¦(p) that expresses demand x as a function of price p. Give the domain of ï¦(p).

> An experiment consists of rolling two fair (not weighted) 4-sided dice and adding the dots on the two sides facing up. Each die is numbered 1–4. Compute the probability of obtaining the indicated sums. 7

> Use the given equation, which expresses price p as a function of demand x, to find a function ï¦(p) that expresses demand x as a function of price p. Give the domain of ï¦(p).

> A model for the number of aggravated assaults per 1,000 population in the United States (Table 4) is a(t) = 5.9 - 1.1 ln t where t is years since 1990. Find the relative rate of change for assaults in 2025.

> A model for Mexicoâs population (Table 3) is ï¦(t) = 1.49t + 38.8 where t is years since 1960. Find and graph the percentage rate of change of ï¦(t) for 0 â¤ t â&curr

> Refer to Problem 87. What price will maximize the revenue from selling fries? Data from Problem 87: The price–demand equation for an order of fries at a fast-food restaurant is x + 1,000p = 2,500 Currently, the price of an order of fries is $0.99. If th

> Refer to Problem 87. If the current price of an order of fries is $1.49, will a 10% price decrease cause revenue to increase or decrease? Data from Problem 87: The price–demand equation for an order of fries at a fast-food restaurant is x + 1,000p = 2,5

> Revenue and elasticity. Refer to Problem 85. If the current price of a hamburger is $4.00, will a 10% price increase cause revenue to increase or decrease? Data from Problem 85: The price–demand equation for hamburgers at a fast-food restaurant is x + 4

> The fast-food restaurant in Problem 83 can produce an order of fries for $0.80. If the restaurant’s daily sales are increasing at the rate of 45 orders of fries per day, how fast is its daily cost for fries increasing?

> Find E(p) for x = (p) = Ae-kp, where A and k are positive constants.

> In a group of n people (n ≤ 100), each person is asked to select a number between 1 and 100, write the number on a slip in a hat. What is the probability that at least 2 of the slips in the hat have the same number written on them?

> use the priceâdemand equation to find the values of x for which demand is elastic and for which demand is inelastic.

> If a priceâdemand equation is solved for p, then price is expressed as p = g1x2 and x becomes the independent variable. In this case, it can be shown that the elasticity of demand is given by use the priceâdemand equat

> use the demand equation to find the revenue function. Sketch the graph of the revenue function, and indicate the regions of inelastic and elastic demand on the graph.

> Use the priceâdemand equation to find the values of p for which demand is elastic and the values for which demand is inelastic. Assume that price and demand are both positive.

> An experiment consists of rolling two fair (not weighted) 4-sided dice and adding the dots on the two sides facing up. Each die is numbered 1–4. Compute the probability of obtaining the indicated sums. 5

> Use the priceâdemand equation to find the values of p for which demand is elastic and the values for which demand is inelastic. Assume that price and demand are both positive.

> use the price–demand equation p + 0.004x = 32, 0 ≤ p ≤ 32. If p = $21 and the price is decreased, will revenue increase or decrease?

> use the price–demand equation p + 0.004x = 32, 0 ≤ p ≤ 32. Find all values of p for which demand is inelastic.

Question: use a graphing calculator to approximate the