Question: use the price–demand equation to find
use the price–demand equation to find the values of x for which demand is elastic and for which demand is inelastic.
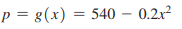
> use the given graph of y = ′(x) to find the intervals on which  is increasing, the intervals on which  is decreasing, and the x coordinates of the local extrema of ï‚
> use the given graph of y = ′(x) to find the intervals on which  is increasing, the intervals on which  is decreasing, and the x coordinates of the local extrema of ï‚
> use the given graph of y = ′(x) to find the intervals on which  is increasing, the intervals on which  is decreasing, and the x coordinates of the local extrema of ï‚
> involve functions 1-6 and their derivatives, g1-g6. Use the graphs shown in figures (A) and (B) to match each function fi with its derivative gj . 
> Consider the command in Figure A and the associated statistical plot in Figure B. (A) Explain why the command does not simulate 50 repetitions of rolling a pair of dice and recording their sum. (B) Describe an experiment that is simulated by this comma
> involve functions 1-6 and their derivatives, g1-g6. Use the graphs shown in figures (A) and (B) to match each function fi with its derivative gj . 
> involve functions 1-6 and their derivatives, g1-g6. Use the graphs shown in figures (A) and (B) to match each function fi with its derivative gj . 
> (x) is continuous on (-∞, ∞). Use the given information to sketch the graph of .
> (x) is continuous on (-∞, ∞). Use the given information to sketch the graph of .
> (x) is continuous on (-∞, ∞). Use the given information to sketch the graph of .
> (x) is continuous on (-∞, ∞). Use the given information to sketch the graph of .
> use a graphing calculator to approximate the critical numbers of (x) to two decimal places. Find the intervals on which (x) is increasing, the intervals on which (x) is decreasing, and the loc
> use a graphing calculator to approximate the critical numbers of (x) to two decimal places. Find the intervals on which (x) is increasing, the intervals on which (x) is decreasing, and the loc
> Find the intervals on which (x) is increasing and the intervals on which (x) is decreasing. Then sketch the graph. Add horizontal tangent lines.
> Find the intervals on which (x) is increasing and the intervals on which (x) is decreasing. Then sketch the graph. Add horizontal tangent lines.
> An experiment consists of rolling two fair (not weighted) 4-sided dice and adding the dots on the two sides facing up. Each die is numbered 1–4. Compute the probability of obtaining the indicated sums. An even sum.
> Find the intervals on which (x) is increasing and the intervals on which (x) is decreasing. Then sketch the graph. Add horizontal tangent lines.
> Find the intervals on which (x) is increasing and the intervals on which (x) is decreasing. Then sketch the graph. Add horizontal tangent lines.
> Find the intervals on which (x) is increasing, the intervals on which (x) is decreasing, and the local extrema.
> Find the intervals on which (x) is increasing, the intervals on which (x) is decreasing, and the local extrema.
> Find the intervals on which (x) is increasing, the intervals on which (x) is decreasing, and the local extrema.
> Find the intervals on which (x) is increasing, the intervals on which (x) is decreasing, and the local extrema.
> Find the intervals on which (x) is increasing, the intervals on which (x) is decreasing, and the local extrema.
> Find the intervals on which (x) is increasing, the intervals on which (x) is decreasing, and the local extrema.
> Find the intervals on which (x) is increasing, the intervals on which (x) is decreasing, and the local extrema.
> Find the intervals on which (x) is increasing, the intervals on which (x) is decreasing, and the local extrema.
> Solve the equation P (E) /P (E’) = a/b for P (E). If P (E) = c/d, show that odds in favor of E occurring are c to d – c.
> Find (A) ′(x), (B) the partition numbers for ′, and (C) the critical numbers of  .
> Find (A) ′(x), (B) the partition numbers for ′, and (C) the critical numbers of  .
> Find (A) ′(x), (B) the partition numbers for ′, and (C) the critical numbers of  .
> Give the local extrema of f and match the graph of  with one of the sign charts a–h.
> Give the local extrema of f and match the graph of  with one of the sign charts a–h.
> Give the local extrema of f and match the graph of  with one of the sign charts a–h.
> Give the local extrema of f and match the graph of  with one of the sign charts a–h.
> Find the relative rate of change of (x).
> Find the relative rate of change of (x).
> Use the given equation, which expresses price p as a function of demand x, to find a function (p) that expresses demand x as a function of price p. Give the domain of (p).
> An experiment consists of rolling two fair (not weighted) 4-sided dice and adding the dots on the two sides facing up. Each die is numbered 1–4. Compute the probability of obtaining the indicated sums. 7
> Use the given equation, which expresses price p as a function of demand x, to find a function (p) that expresses demand x as a function of price p. Give the domain of (p).
> Use the given equation, which expresses price p as a function of demand x, to find a function (p) that expresses demand x as a function of price p. Give the domain of (p).
> Use the given equation, which expresses price p as a function of demand x, to find a function (p) that expresses demand x as a function of price p. Give the domain of (p).
> A model for the number of aggravated assaults per 1,000 population in the United States (Table 4) is a(t) = 5.9 - 1.1 ln t where t is years since 1990. Find the relative rate of change for assaults in 2025.
> A model for Mexico’s population (Table 3) is (t) = 1.49t + 38.8 where t is years since 1960. Find and graph the percentage rate of change of (t) for 0 ≤ t â‰&curr
> Refer to Problem 87. What price will maximize the revenue from selling fries? Data from Problem 87: The price–demand equation for an order of fries at a fast-food restaurant is x + 1,000p = 2,500 Currently, the price of an order of fries is $0.99. If th
> Refer to Problem 87. If the current price of an order of fries is $1.49, will a 10% price decrease cause revenue to increase or decrease? Data from Problem 87: The price–demand equation for an order of fries at a fast-food restaurant is x + 1,000p = 2,5
> Revenue and elasticity. Refer to Problem 85. If the current price of a hamburger is $4.00, will a 10% price increase cause revenue to increase or decrease? Data from Problem 85: The price–demand equation for hamburgers at a fast-food restaurant is x + 4
> The fast-food restaurant in Problem 83 can produce an order of fries for $0.80. If the restaurant’s daily sales are increasing at the rate of 45 orders of fries per day, how fast is its daily cost for fries increasing?
> Find E(p) for x = (p) = Ae-kp, where A and k are positive constants.
> In a group of n people (n ≤ 100), each person is asked to select a number between 1 and 100, write the number on a slip in a hat. What is the probability that at least 2 of the slips in the hat have the same number written on them?
> use the price–demand equation to find the values of x for which demand is elastic and for which demand is inelastic.
> If a price–demand equation is solved for p, then price is expressed as p = g1x2 and x becomes the independent variable. In this case, it can be shown that the elasticity of demand is given by use the price–demand equat
> If a price–demand equation is solved for p, then price is expressed as p = g1x2 and x becomes the independent variable. In this case, it can be shown that the elasticity of demand is given by use the price–demand equat
> use the demand equation to find the revenue function. Sketch the graph of the revenue function, and indicate the regions of inelastic and elastic demand on the graph.
> use the demand equation to find the revenue function. Sketch the graph of the revenue function, and indicate the regions of inelastic and elastic demand on the graph.
> use the demand equation to find the revenue function. Sketch the graph of the revenue function, and indicate the regions of inelastic and elastic demand on the graph.
> Use the price–demand equation to find the values of p for which demand is elastic and the values for which demand is inelastic. Assume that price and demand are both positive.
> Use the price–demand equation to find the values of p for which demand is elastic and the values for which demand is inelastic. Assume that price and demand are both positive.
> Use the price–demand equation to find the values of p for which demand is elastic and the values for which demand is inelastic. Assume that price and demand are both positive.
> An experiment consists of rolling two fair (not weighted) 4-sided dice and adding the dots on the two sides facing up. Each die is numbered 1–4. Compute the probability of obtaining the indicated sums. 5
> Use the price–demand equation to find the values of p for which demand is elastic and the values for which demand is inelastic. Assume that price and demand are both positive.
> use the price–demand equation p + 0.004x = 32, 0 ≤ p ≤ 32. If p = $21 and the price is decreased, will revenue increase or decrease?
> use the price–demand equation p + 0.004x = 32, 0 ≤ p ≤ 32. Find all values of p for which demand is inelastic.
> use the price–demand equation p + 0.004x = 32, 0 ≤ p ≤ 32. Find the elasticity of demand when p = $16. If the $16 price is increased by 9%, what is the approximate percentage change in demand?
> use the price–demand equation p + 0.004x = 32, 0 ≤ p ≤ 32. Find the elasticity of demand when p = $28. If the $28 price is decreased by 6%, what is the approximate percentage change in demand?
> use the price–demand equation to determine whether demand is elastic, is inelastic, or has unit elasticity at the indicated values of p.
> use the price–demand equation to determine whether demand is elastic, is inelastic, or has unit elasticity at the indicated values of p.
> Find the logarithmic derivative.
> Find the logarithmic derivative.
> Find the logarithmic derivative.
>
> Find the logarithmic derivative.
> use the price–demand equation to find E(p), the elasticity of demand.
> use the price–demand equation to find E(p), the elasticity of demand.
> use the price–demand equation to find E(p), the elasticity of demand.
> Find the percentage rate of change of (x) at the indicated value of x. Round to the nearest tenth of a percent.
> Find the percentage rate of change of (x) at the indicated value of x. Round to the nearest tenth of a percent.
> Find the percentage rate of change of (x) at the indicated value of x. Round to the nearest tenth of a percent.
> Find the percentage rate of change of (x) at the indicated value of x. Round to the nearest tenth of a percent.
> Find the relative rate of change of (x) at the indicated value of x. Round to three decimal places.
> Find the relative rate of change of (x) at the indicated value of x. Round to three decimal places.
> An experiment consists of rolling two fair (not weighted) 4-sided dice and adding the dots on the two sides facing up. Each die is numbered 1–4. Compute the probability of obtaining the indicated sums. 3
> Find the relative rate of change of (x) at the indicated value of x. Round to three decimal places.
> Find the relative rate of change of (x) at the indicated value of x. Round to three decimal places.
> Find the relative rate of change of (x) at the indicated value of x. Round to three decimal places.
> Find the relative rate of change of (x).
> Assume that x = x(t) and y = y(t). Find the indicated rate, given the other information. y = x3 - 3; dx/dt = -2 when x = 2; find dy/dt
> The height of a right circular cylinder is twice its radius. If the volume is 1,000 cubic meters, find the radius and height to the nearest hundredth of a meter.
> The radius of a spherical balloon is 3 meters. Find its volume to the nearest tenth of a cubic meter.
> The legs of a right triangle have lengths 54 feet and 69 feet. Find the length of the hypotenuse to the nearest foot.
> A central pivot irrigation system covers a circle of radius 400 meters. Find the area of the circle to the nearest square meter.
> A person who is new on an assembly line performs an operation in T minutes after x performances of the operation, as given by operations per hours, where t is time in hours, find dT/dt after 36 performances of the operation
> Explain how the three events A, B, and C from a sample space S are related to each other in order for the following equation to hold true:
> A circular spinner is divided into 15 sectors of equal area: 6 red sectors, 5 blue, 3 yellow, and 1 green. , consider the experiment of spinning the spinner once. Find the probability that the spinner lands on: Yellow.
> Price–demand. Repeat Problem 45 for x2 + 2xp + 25p2 = 74,500 Data from Problem 45: The price p (in dollars) and demand x for a product are related by 2x2 + 5xp + 50p2 = 80,000 (A) If the price is increasing at a rate of $2 per month when the price is
> Political campaign. Refer to Problem 43. If $20 million has been spent on television advertising and the rate of spending is $6 million per week, at what rate (in percentage points per week) will the polling percentage increase? Data from Problem 43: A
> The price p (in dollars) and demand x (in bushels) for peaches are related by x = 3p2 - 2p + 500 If the current price of $38 per bushel is decreasing at a rate of $1.50 per week, find the rate of change (in bushels per week) of the supply.
> Refer to Problem 38. Find the associated revenue function R(p) and the rate of change (in dollars per week) of the revenue. Data from Problem 38: The price p (in dollars) and demand x for microwave ovens are related by
> The price p (in dollars) and demand x for microwave ovens are related by If the current price of $124 is increasing at a rate of $3 per week, find the rate of change (in ovens per week) of the demand.
> Repeat Problem 35 for s = 50,000 - 20,000e-0.0004x Data from Problem 35: A retail store estimates that weekly sales s and weekly advertising costs x (both in dollars) are related by s = 60,000 - 40,000e-0.0005x The current weekly advertising costs are
> Cost, revenue, and profit rates. Repeat Problem 33 for C = 72,000 + 60x R = 200x - x2 30 P = R - C where production is increasing at a rate of 500 calculators per week at a production level of 1,500 calculators. Data from Problem 33: Suppose that for a

