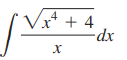[SOLVED] use substitution techniques and Table 1 to

> Find a formula for the function V(d, h) of two variables that gives the volume of a right circular cylinder of diameter d and height h.

> find the indicated function f of a single variable.

> find the indicated value of the given function.

> Find each indefinite integral. Check by differentiating.

> find the indicated value of the given function.

> find the indicated values of ((x, y, z) = 2x - 3y2 + 5z3 – 1 ((-10, 4, -3)

> find the indicated values of ((x, y, z) = 2x - 3y2 + 5z3 – 1 ((0, 0, 2)

> Find the indicated values of the functions g(0, 0)

> Find the indicated values of the functions g (-2, 0)

> Find the indicated values of the functions

> find the indicated value of the function of two or three variables. The height of a right circular cone is 42 inches and the radius is 7 inches. Find the volume.

> Find each indefinite integral and check the result by differentiating.

> Use Table 1 in Appendix C to find each indefinite integral //

> Round function values to four decimal places and the final answer to two decimal places. Use Simpsonâs rule with n = 2 (so there are 2n = 4 subintervals) to approximate

> Round function values to four decimal places and the final answer to two decimal places. Use Simpsonâs rule with n = 1 (so there are 2n = 2 subintervals) to approximate.

> Round function values to four decimal places and the final answer to two decimal places. Use the trapezoidal rule with n = 4 to approximate

> Round function values to four decimal places and the final answer to two decimal places.

> For the voters of Problem 92, graph y = ((t) and the line representing the average number of voters over the interval [0, 10] in the same coordinate system. Describe how the areas under the two curves over the interval [0, 10] are related. Data from Pro

> The number of voters (in thousands) in a metropolitan area is given approximately by where t is time in years. Find the average number of voters during the period from t = 0 to t = 10.

> The concentration of particulate matter (in parts per million) during a 24-hour period is given approximately by where t is time in hours. Find the average concentration during the period from t = 0 to t = 24.

> The marginal revenue for a company that manufactures and sells x graphing calculators per week is given by where R(x) is the revenue in dollars. Find the revenue function and the number of calculators that must be sold (to the nearest unit) to produce

> For the motor oil of Problem 84, graph theÂ priceâdemand equation and the line representing the average price in the same coordinate system over the interval [50, 250]. Describe how the areas under the two curves over the int

> Find each indefinite integral. Check by differentiating.

> At a discount department store, the priceâ demand equation for premium motor oil is given by where x is the number of cans of oil that can be sold at a price of $p. Find the average price over the demand interval [50, 250].

> Graph y = x and the Lorenz curve of Problem 80 over the interval [0, 1]. Discuss the effect of the area bounded by y = x and the Lorenz curve getting larger relative to the equitable distribution of income.

> Find the Gini index of income concentration for the Lorenz curve with equation.

> Find the interest earned at 3.7%, compounded continuously, for 5 years for the continuous income stream with rate of flow ((t) = 200t.

> A company manufactures a portable DVD player. It has fixed costs of $11,000 per week and a marginal cost given by where C(x) is the total cost per week at an output of x players per week. Find the cost function C(x) and determine the production level (

> Graph the price–supply equation and the price-level equation p = 20 of Problem 72 in the same coordinate system. What region represents the producers’ surplus?

> Find the producersâ surplus at a price level of p = $20 for the priceâsupply equation

> Find the area bounded by the graphs of y = ((x) and y = g(x) to two decimal places. Use a graphing calculator to approximate intersection points to two decimal places.

> If ((x) = ax3 + bx2 + cx + d, where a, b, c, and d are any real numbers, use Simpsonâs rule with n = 1 (so there are 2n = 2 subintervals) to show that

> use the chain rule to find the derivative of each function.

> Problems are mixedâsome require the use of Table 1, and others can be solved with techniques considered earlier.

> use Table 1 to find each indefinite integral.

> use substitution techniques and Table 1 to find each indefinite integral.

> write each function as a sum of terms of the form axn , where a is a constant.

> use substitution techniques and Table 1 to find each indefinite integral.

> Show that Simpson’s rule with n = 1 (so there are 2 subintervals) gives the exact value of ∫5 1 (3x2 - 4x + 72 dx.

> Show that Simpson’s rule with n = 3 (so there are 6 subintervals) gives the exact value of ∫5 -1 (3 - 2x) dx.

> Let ((x) = 10 - 3x and suppose that the interval [5, 75] is partitioned into 35 subintervals of length 2. Without calculating T35, explain why the trapezoidal rule gives the negative of the exact area between the graph of f and the x axis from x = 5 to x

> Use Simpsonâs rule with n = 4 (so there are 2n = 8 subintervals) to approximate and use the fundamental theorem of calculus to find the exact value of the definite integral.

> Use the trapezoidal rule with n = 5 to approximate ∫111 x3 dx and use the fundamental theorem of calculus to find the exact value of the definite integral.

> Use Table 1 in Appendix C to find the antiderivative. //

> use the chain rule to find the derivative of each function.

> could the given matrix be the transition matrix of an absorbing Markov chain?

> Use Table 1 in Appendix C to find the antiderivative. //

> Use Table 1 in Appendix C to find each indefinite integral //

> Find the derivative of ï¦(x) and the indefinite integral of g(x).

> write each function as a sum of terms of the form axn , where a is a constant.

> A student enrolled in a steno typing class progressed at a rate of N′(t) = (t + 10)e-0.1t words per minute per week t weeks after enrolling in a 15- week course. If a student had no knowledge of steno typing (that is, if the student could stenotype at

> After a person takes a pill, the drug contained in the pill is assimilated into the bloodstream. The rate of assimilation t minutes after taking the pill is R(t) = te-0.2t Find the total amount of the drug that is assimilated into the bloodstream durin

> Interpret the results of Problem 84 with both a graph and a description of the graph. Data from Problem 84: Find the producers’ surplus (to the nearest dollar) at a price level of p = $26 for the price–supply equation p = S(x) = 5 ln (x + 1) Use x com

> Find the producers’ surplus (to the nearest dollar) at a price level of p = $26 for the price–supply equation p = S(x) = 5 ln (x + 1) Use x computed to the nearest higher unit.

> The rate of change of the monthly sales of a new basketball game is given by S′(t) = 350 ln (t + 1) S(0) = 0 where t is the number of months since the game was released and S(t) is the number of games sold each month. Find S(t). When, to the nearest m

> Interpret the results of Problem 78 with both a graph and a description of the graph. Data from Problem 78: Find the Gini index of income concentration for the Lorenz curve with equation y = x2ex - 1

> Find the Gini index of income concentration for the Lorenz curve with equation y = x2ex - 1

> Find the interest earned at 4.15%, compounded continuously, for 4 years for a continuous income stream with a rate of flow of ((t) = 1,000 - 250t

> Interpret the results of Problem 72 with both a graph and a description of the graph.

> An oil field is estimated to produce oil at a rate of R1t2 thousand barrels per month t months from now, as given by R(t) = 10te-0.1t Use an appropriate definite integral to find the total production (to the nearest thousand barrels) in the first year

> use the chain rule to find the derivative of each function.

> use absolute value on a graphing calculator to find the area between the curve and the x axis over the given interval. Find answers to two decimal places.

> Problems are mixedâsome may require use of the integration by-parts formula along with techniques we have considered earlier; others may require repeated use of the integration-by-parts formula. Assume that g(x) > 0 whenever ln&Acirc

> write each function as a sum of terms of the form axn , where a is a constant.

> Problems are mixedâsome may require use of the integration by-parts formula along with techniques we have considered earlier; others may require repeated use of the integration-by-parts formula. Assume that g(x) > 0 whenever ln&Acirc

Question: use substitution techniques and Table 1 to