Question: Use the definition of a Taylor series
Use the definition of a Taylor series to find the first four nonzero terms of the series for f(x) centered at the given value of a.
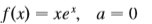
Transcribed Image Text:
> Evaluate the integral. xe 2x (1 + 2x)?
> Use a Maclaurin series to obtain the Maclaurin series for the given function. S(a) — sin(тx/4)
> Use a Maclaurin series to obtain the Maclaurin series for the given function. f(x) = arctan(x²)
> Use the Root Test to determine whether the series is convergent or divergent. Σ (arctan n"
> Use the Root Test to determine whether the series is convergent or divergent. (-2)" Σ n"
> Use the Ratio Test to determine whether the series is convergent or divergent. n! 100"
> Find the radius of convergence and interval of convergence of the series. 2 n"x" -1
> Test the series for convergence or divergence. e 2 一1 1
> Use a Maclaurin series to obtain the Maclaurin series for the given function. S(x)- = x cos(}x²)
> Use the Alternating Series Estimation Theorem or Taylor’s Inequality to estimate the range of values of x for which the given approximation is accurate to within the stated error. Check your answer graphically. cos x = 1 2 (lerror|<
> Evaluate the integral. x tan?x dx
> Use a Maclaurin series to obtain the Maclaurin series for the given function. f(x) x cos 2x
> The Bessel function of order 1 is defined by (a) Show that J1 satisfies the differential equation (b) Show that / (-1)"x²*+1 J,(x) = E n! (n + 1)!2²n*! x*I"(x) + xJ{(x) + (x² – 1)J,(x) = 0
> (a) Show that J0 (the Bessel function of order 0 given in Example 4) satisfies the differential equation (b) Evaluate / correct to three decimal places. X²JF(x) + x.JK(x) + x³J(x) = 0
> Use the binomial series to expand the function as a power series. State the radius of convergence. (1 – x)/4
> Use the binomial series to expand the function as a power series. State the radius of convergence. 1 (2 + x)
> Use the binomial series to expand the function as a power series. State the radius of convergence. V8 + x
> Use the binomial series to expand the function as a power series. State the radius of convergence. V1 - x
> Prove that the series obtained in Exercise 18 represents cosh x for all x. Data from Exercise 18: Find the Maclaurin series for f(x) using the definition of a Maclaurin series. [Assume that f has a power series expansion. Do not show that Rn(x) â
> Prove that the series obtained in Exercise 17 represents sinh x for all x. Data from Exercise 17: Find the Maclaurin series for f(x) using the definition of a Maclaurin series. [Assume that f has a power series expansion. Do not show that Rn(x) â
> Evaluate the integral. z³e² dz
> Use the Alternating Series Estimation Theorem or Taylor’s Inequality to estimate the range of values of x for which the given approximation is accurate to within the stated error. Check your answer graphically. sin x = x - (lerror|
> Prove that the series obtained in Exercise 25 represents sin x for all x. Data from Exercise 25: Find the Taylor series for f(x) centered at the given value of a. [Assume that f has a power series expansion. Do not show that Rn(x) → 0
> Prove that the series obtained in Exercise 13 represents cos x for all x. Data from Exercise 13: Find the Maclaurin series for f(x) using the definition of a Maclaurin series. [Assume that f has a power series expansion. Do not show that Rn(x) â&
> Find the Taylor series for f(x) centered at the given value of a. [Assume that f has a power series expansion. Do not show that Rn(x) → 0.] Also find the associated radius of convergence. S(x) = Vx, a = 16
> Find the Taylor series for f(x) centered at the given value of a. [Assume that f has a power series expansion. Do not show that Rn(x) → 0.] Also find the associated radius of convergence. f(x) = sin x, a = T а —
> Find the Taylor series for f(x) centered at the given value of a. [Assume that f has a power series expansion. Do not show that Rn(x) → 0.] Also find the associated radius of convergence. f(x) = cos x, a= /2 a = "/2
> Find the Taylor series for f(x) centered at the given value of a. [Assume that f has a power series expansion. Do not show that Rn(x) → 0.] Also find the associated radius of convergence. f(x) — е", а — 3 %3D
> Find the Taylor series for f(x) centered at the given value of a. [Assume that f has a power series expansion. Do not show that Rn(x) → 0.] Also find the associated radius of convergence. f(x) — 1/x, а —-3 a
> Find the Taylor series for f(x) centered at the given value of a. [Assume that f has a power series expansion. Do not show that Rn(x) → 0.] Also find the associated radius of convergence. f(x) — In x, а — 2
> Find the Taylor series for f(x) centered at the given value of a. [Assume that f has a power series expansion. Do not show that Rn(x) → 0.] Also find the associated radius of convergence. f(x) = x — х* — х* + 2, а—-2
> Evaluate the integral. Se°cos 20 do
> Find the Taylor series for f(x) centered at the given value of a. [Assume that f has a power series expansion. Do not show that Rn(x) → 0.] Also find the associated radius of convergence. f(x) = x* + 2x³ + x, a = 2
> How many terms of the Maclaurin series for ln(1 + x) do you need to use to estimate ln 1.4 to within 0.001?
> Find the Maclaurin series for f(x) using the definition of a Maclaurin series. [Assume that f has a power series expansion. Do not show that Rn(x) → 0.] Also find the associated radius of convergence. f(x) = cosh x
> Find the Maclaurin series for f(x) using the definition of a Maclaurin series. [Assume that f has a power series expansion. Do not show that Rn(x) → 0.] Also find the associated radius of convergence. f(x) = sinh x
> Find the Maclaurin series for f(x) using the definition of a Maclaurin series. [Assume that f has a power series expansion. Do not show that Rn(x) → 0.] Also find the associated radius of convergence. f(x) - x cos x
> Find the Maclaurin series for f(x) using the definition of a Maclaurin series. [Assume that f has a power series expansion. Do not show that Rn(x) → 0.] Also find the associated radius of convergence. S(x) = 2"
> Find the Maclaurin series for f(x) using the definition of a Maclaurin series. [Assume that f has a power series expansion. Do not show that Rn(x) → 0.] Also find the associated radius of convergence. f(x) = e-24
> Find the Maclaurin series for f(x) using the definition of a Maclaurin series. [Assume that f has a power series expansion. Do not show that Rn(x) → 0.] Also find the associated radius of convergence. f(x) = cos x
> Find the Maclaurin series for f(x) using the definition of a Maclaurin series. [Assume that f has a power series expansion. Do not show that Rn(x) → 0.] Also find the associated radius of convergence. f(x) = In(1 + x)
> Find the Maclaurin series for f(x) using the definition of a Maclaurin series. [Assume that f has a power series expansion. Do not show that Rn(x) → 0.] Also find the associated radius of convergence. -2 f(x) = (1 – x) ?
> Evaluate the integral. e 20 sin 30 d0
> Use the definition of a Taylor series to find the first four nonzero terms of the series for f(x) centered at the given value of a. f(x) — сos?x, а — 0 = cos
> Use the definition of a Taylor series to find the first four nonzero terms of the series for f(x) centered at the given value of a. f(x) — sin x, а — п/6
> Use Taylor’s Inequality to determine the number of terms of the Maclaurin series for ex that should be used to estimate e0.1 to within 0.00001.
> Use the definition of a Taylor series to find the first four nonzero terms of the series for f(x) centered at the given value of a. f(x) — In x, а — 1
> Use the definition of a Taylor series to find the first four nonzero terms of the series for f(x) centered at the given value of a. f(x) — Vх, а —8
> Use the definition of a Taylor series to find the first four nonzero terms of the series for f(x) centered at the given value of a. 1 S(x) a = 2 1 + x'
> Find the Taylor series for f centered at 4 if What is the radius of convergence of the Taylor series? (-1)" n! f(4) 3"(n + 1)
> If f (n)(0) = ( n+1)! for n = 0, 1, 2, ……, find the Maclaurin series for f and its radius of convergence.
> The graph off is shown. (a) Explain why the series is not the Taylor series of f centered at 1. (b) Explain why the series is not the Taylor series of f centered at 2. y f 1 1.6 – 0.8(x – 1) + 0.4(x – 1)? – 0.1(x – 1)³ + ... 2.8 + 0.5(x – 2) + 1.5(
> Evaluate the integral. dz 107
> Test the series for convergence or divergence. п — 1 n-1 n° +1
> Test the series for convergence or divergence. n? – 1 -1 n° + 1
> Use the information from Exercise 16 to estimate sin 38° correct to five decimal places. Data from Exercise 16: (a) Approximate f by a Taylor polynomial with degree n at the number a. (b) Use Taylor’s Inequality to estimate
> Use any test to determine whether the series is absolutely convergent, conditionally convergent, or divergent. (-1)" –1)" -2 п In n
> Use any test to determine whether the series is absolutely convergent, conditionally convergent, or divergent. sin(nT/6) 1 + n/n R-1
> Use any test to determine whether the series is absolutely convergent, conditionally convergent, or divergent. Σ -2In n
> Use any test to determine whether the series is absolutely convergent, conditionally convergent, or divergent. n52n 10**1 n+1
> Use the Ratio Test to determine whether the series is convergent or divergent. 2.4· 6. .... (2n) Σ n!
> Use the Ratio Test to determine whether the series is convergent or divergent. 2.5· 8· 11 3. 5·7.9 2 2·5 2 ·5- 8 3 3. 5 3.5.7 +
> Evaluate the integral. | (In x)°dx
> Use the Ratio Test to determine whether the series is convergent or divergent. 2! 3! 4! 1:3 1.3. 5 1:3. 5·7 п! + (-1)"-1. + 1. 3· 5. .... (2n – 1)
> Use the Ratio Test to determine whether the series is convergent or divergent. (2n)! Σ (л!)? n=1
> Use the Ratio Test to determine whether the series is convergent or divergent. n 100 100" Σ n!
> Use the Ratio Test to determine whether the series is convergent or divergent. の n!
> Use the information from Exercise 5 to estimate cos 80° correct to five decimal places. Data from Exercise 5: Find the Taylor polynomial T3(x) for the function f centered at the number a. Graph f and T3 on the same screen. f(x) cos х, a
> Use the Ratio Test to determine whether the series is convergent or divergent. cos(nп/3) n!
> Use the Ratio Test to determine whether the series is convergent or divergent. 10 (-10)**1 n+1 n-1
> Use the Ratio Test to determine whether the series is convergent or divergent. nT" Σ (-3)ª-| R-1
> Use the Ratio Test to determine whether the series is convergent or divergent. 10" Σ (п + 1)42я1 R-1
> Use the Ratio Test to determine whether the series is convergent or divergent. E ke * k-1
> Evaluate the integral. |x cosh ax dx
> Use the Ratio Test to determine whether the series is convergent or divergent. 00 k= k!
> Calculate 20 or 30 terms of the sequence for p0 = 1 2 and for two values of k such that 1 < k < 3. Graph each sequence. Do the sequences appear to converge? Repeat for a different value of p0 between 0 and 1. Does the limit depend on the choice of p0?
> A sub tangent is a portion of the x-axis that lies directly beneath the segment of a tangent line from the point of contact to the x-axis. Find the curves that pass through the point (c, 1) and whose sub tangents all have length c.
> Find the curve y = f(x) such that f(x) > 0, f(0) − 0, f(1) = 1, and the area under the graph off from 0 to x is proportional to the (n + 1)st power of f(x).
> Find all functions f that satisfy the equation ) dx dx f(x) -1
> Let f be a function with the property that f(0) = 1, f’(0) = 1, and f(a+b) = f(a) f(b) for all real numbers a and b. Show that / for all x and deduce that /
> A student forgot the Product Rule for differentiation and made the mistake of thinking that / However, he was lucky and got the correct answer. The function f that he used was / and the domain of his problem was the interval / .What was the function t?
> Find all functions f such that f is continuous and [f(x)]² = 100 + * {[SM)² + [SOI*} dt for all real x
> Find all curves with the property that if a line is drawn from the origin to any point (x, y) on the curve, and then a tangent is drawn to the curve at that point and extended to meet the x-axis, the result is an isosceles triangle with equal sides meeti
> Find all curves with the property that if the normal line is drawn at any point P on the curve, then the part of the normal line between P and the x-axis is bisected by the y-axis.
> Evaluate the integral. Ste * dt
> Evaluate the integral. ,0.2y dy
> Evaluate the integral. Jx cos 5x dx
> Evaluate the integral using integration by parts with the indicated choices of u and dv. ( Vĩ In x dx; u = In x, dv = /x dx
> A finite Fourier series is given by the sum Show that the mth coefficient am is given by the formula N f(x) = E a, sin nx - a, sin x + a2 sin 2x + · · · + an sin Nx f(x) sin mx dx
> Prove the formula, where m and n are positive integers. 0if m+n п if m — п cos mx cos nx dx
> Prove the formula, where m and n are positive integers. So if m +n " sin mx sin nx dx T if m = n
> Prove the formula, where m and n are positive integers. T" sin mx cos nx dx = 0
> Household electricity is supplied in the form of alternating current that varies from 155 V to 2155 V with a frequency of 60 cycles per second (Hz). The voltage is thus given by the equation where t is the time in seconds. Voltmeters read the RMS (root-m
> Find the volume obtained by rotating the region bounded by the curves about the given axis. у — sec x, у — cos x, 0 <x< п/3; about y —-1
> Find the volume obtained by rotating the region bounded by the curves about the given axis. y = sin x, y = cos x, 0 < x </4; _about y 1
> Find the volume obtained by rotating the region bounded by the curves about the given axis. y = sin?x, y = 0, 0<x< ™; about the x-axis
> Use a graph of the integrand to guess the value of the integral. Then use the methods of this section to prove that your guess is correct. sin 27x cos 5T x dx Jo
> Use a graph of the integrand to guess the value of the integral. Then use the methods of this section to prove that your guess is correct. *2m cos'x dx Jo
> Find the area of the region bounded by the given curves. y tan x, y = tan?x, 0<x T/4
> Find the area of the region bounded by the given curves. y = sin?x, y = sin'x, 0<x< T

