Question: Find the volume obtained by rotating the
Find the volume obtained by rotating the region bounded by the curves about the given axis.
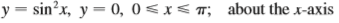
Transcribed Image Text:
y = sin?x, y = 0, 0
> Use the definition of a Taylor series to find the first four nonzero terms of the series for f(x) centered at the given value of a. f(x) — Vх, а —8
> Use the definition of a Taylor series to find the first four nonzero terms of the series for f(x) centered at the given value of a. 1 S(x) a = 2 1 + x'
> Use the definition of a Taylor series to find the first four nonzero terms of the series for f(x) centered at the given value of a.
> Find the Taylor series for f centered at 4 if What is the radius of convergence of the Taylor series? (-1)" n! f(4) 3"(n + 1)
> If f (n)(0) = ( n+1)! for n = 0, 1, 2, ……, find the Maclaurin series for f and its radius of convergence.
> The graph off is shown. (a) Explain why the series is not the Taylor series of f centered at 1. (b) Explain why the series is not the Taylor series of f centered at 2. y f 1 1.6 – 0.8(x – 1) + 0.4(x – 1)? – 0.1(x – 1)³ + ... 2.8 + 0.5(x – 2) + 1.5(
> Evaluate the integral. dz 107
> Test the series for convergence or divergence. п — 1 n-1 n° +1
> Test the series for convergence or divergence. n? – 1 -1 n° + 1
> Use the information from Exercise 16 to estimate sin 38° correct to five decimal places. Data from Exercise 16: (a) Approximate f by a Taylor polynomial with degree n at the number a. (b) Use Taylor’s Inequality to estimate
> Use any test to determine whether the series is absolutely convergent, conditionally convergent, or divergent. (-1)" –1)" -2 п In n
> Use any test to determine whether the series is absolutely convergent, conditionally convergent, or divergent. sin(nT/6) 1 + n/n R-1
> Use any test to determine whether the series is absolutely convergent, conditionally convergent, or divergent. Σ -2In n
> Use any test to determine whether the series is absolutely convergent, conditionally convergent, or divergent. n52n 10**1 n+1
> Use the Ratio Test to determine whether the series is convergent or divergent. 2.4· 6. .... (2n) Σ n!
> Use the Ratio Test to determine whether the series is convergent or divergent. 2.5· 8· 11 3. 5·7.9 2 2·5 2 ·5- 8 3 3. 5 3.5.7 +
> Evaluate the integral. | (In x)°dx
> Use the Ratio Test to determine whether the series is convergent or divergent. 2! 3! 4! 1:3 1.3. 5 1:3. 5·7 п! + (-1)"-1. + 1. 3· 5. .... (2n – 1)
> Use the Ratio Test to determine whether the series is convergent or divergent. (2n)! Σ (л!)? n=1
> Use the Ratio Test to determine whether the series is convergent or divergent. n 100 100" Σ n!
> Use the Ratio Test to determine whether the series is convergent or divergent. の n!
> Use the information from Exercise 5 to estimate cos 80° correct to five decimal places. Data from Exercise 5: Find the Taylor polynomial T3(x) for the function f centered at the number a. Graph f and T3 on the same screen. f(x) cos х, a
> Use the Ratio Test to determine whether the series is convergent or divergent. cos(nп/3) n!
> Use the Ratio Test to determine whether the series is convergent or divergent. 10 (-10)**1 n+1 n-1
> Use the Ratio Test to determine whether the series is convergent or divergent. nT" Σ (-3)ª-| R-1
> Use the Ratio Test to determine whether the series is convergent or divergent. 10" Σ (п + 1)42я1 R-1
> Use the Ratio Test to determine whether the series is convergent or divergent. E ke * k-1
> Evaluate the integral. |x cosh ax dx
> Use the Ratio Test to determine whether the series is convergent or divergent. 00 k= k!
> Calculate 20 or 30 terms of the sequence for p0 = 1 2 and for two values of k such that 1 < k < 3. Graph each sequence. Do the sequences appear to converge? Repeat for a different value of p0 between 0 and 1. Does the limit depend on the choice of p0?
> A sub tangent is a portion of the x-axis that lies directly beneath the segment of a tangent line from the point of contact to the x-axis. Find the curves that pass through the point (c, 1) and whose sub tangents all have length c.
> Find the curve y = f(x) such that f(x) > 0, f(0) − 0, f(1) = 1, and the area under the graph off from 0 to x is proportional to the (n + 1)st power of f(x).
> Find all functions f that satisfy the equation ) dx dx f(x) -1
> Let f be a function with the property that f(0) = 1, f’(0) = 1, and f(a+b) = f(a) f(b) for all real numbers a and b. Show that / for all x and deduce that /
> A student forgot the Product Rule for differentiation and made the mistake of thinking that / However, he was lucky and got the correct answer. The function f that he used was / and the domain of his problem was the interval / .What was the function t?
> Find all functions f such that f is continuous and [f(x)]² = 100 + * {[SM)² + [SOI*} dt for all real x
> Find all curves with the property that if a line is drawn from the origin to any point (x, y) on the curve, and then a tangent is drawn to the curve at that point and extended to meet the x-axis, the result is an isosceles triangle with equal sides meeti
> Find all curves with the property that if the normal line is drawn at any point P on the curve, then the part of the normal line between P and the x-axis is bisected by the y-axis.
> Evaluate the integral. Ste * dt
> Evaluate the integral. ,0.2y dy
> Evaluate the integral. Jx cos 5x dx
> Evaluate the integral using integration by parts with the indicated choices of u and dv. ( Vĩ In x dx; u = In x, dv = /x dx
> A finite Fourier series is given by the sum Show that the mth coefficient am is given by the formula N f(x) = E a, sin nx - a, sin x + a2 sin 2x + · · · + an sin Nx f(x) sin mx dx
> Prove the formula, where m and n are positive integers. 0if m+n п if m — п cos mx cos nx dx
> Prove the formula, where m and n are positive integers. So if m +n " sin mx sin nx dx T if m = n
> Prove the formula, where m and n are positive integers. T" sin mx cos nx dx = 0
> Household electricity is supplied in the form of alternating current that varies from 155 V to 2155 V with a frequency of 60 cycles per second (Hz). The voltage is thus given by the equation where t is the time in seconds. Voltmeters read the RMS (root-m
> Find the volume obtained by rotating the region bounded by the curves about the given axis. у — sec x, у — cos x, 0 <x< п/3; about y —-1
> Find the volume obtained by rotating the region bounded by the curves about the given axis. y = sin x, y = cos x, 0 < x </4; _about y 1
> Use a graph of the integrand to guess the value of the integral. Then use the methods of this section to prove that your guess is correct. sin 27x cos 5T x dx Jo
> Use a graph of the integrand to guess the value of the integral. Then use the methods of this section to prove that your guess is correct. *2m cos'x dx Jo
> Find the area of the region bounded by the given curves. y tan x, y = tan?x, 0<x T/4
> Find the area of the region bounded by the given curves. y = sin?x, y = sin'x, 0<x< T
> Find the average value of the function f(x) = sin2x cos3x on the interval /
> Evaluate the indefinite integral. Illustrate, and check that your answer is reasonable, by graphing both the integrand and its antiderivative (taking C = 0). ( sec“(}x) dx
> Evaluate the indefinite integral. Illustrate, and check that your answer is reasonable, by graphing both the integrand and its antiderivative (taking C = 0). | sin 3x sin 6x dx
> Evaluate the indefinite integral. Illustrate, and check that your answer is reasonable, by graphing both the integrand and its antiderivative (taking C = 0). sin'x cos'x dx
> Prove the Root Test.
> Evaluate the indefinite integral. Illustrate, and check that your answer is reasonable, by graphing both the integrand and its antiderivative (taking C = 0). S x sin?(x²) dx
> Evaluate the integral. Sx tan'x dx
> Evaluate the integral. dx cos x - 1
> Evaluate the integral. *w/4 cos 40 de
> Evaluate the integral. *w/6 1 + cos 2x dx
> Evaluate the integral. *w/2 cos 5t cos 10t dt
> Evaluate the integral. sin 20 sin 60 do
> Evaluate the integral. | sin 8x cos 5x dx
> Evaluate the integral. w/3 csc'x dx Ju/6 (
> Use the sum of the first 10 terms to approximate the sum of the series Use Exercise 46 to estimate the error. Data from Exercise 46: Let / be a series with positive terms and let / Suppose that / converges by the Ratio Test. As usual, we let Rn be the
> Evaluate the integral. csc x dx
> Evaluate the integral. "w/2 csc*0 cot*0 d0 a/4
> Evaluate the integral. *w/2 " cot°o csc'p dp Jm/4
> Evaluate the integral. *w/2 cot'x dx /4
> Evaluate the integral. sin cos'o
> Evaluate the integral. sec x tan x dx
> Evaluate the integral. | tan?x sec x dx
> Evaluate the integral. ( tan'x dx
> Evaluate the integral. w/4 tan't dt
> Evaluate the integral. | dx tan'x sec"x
> (a) Approximate f by a Taylor polynomial with degree n at the number a. (b) Use Taylor’s Inequality to estimate the accuracy of the approximation / when x lies in the given interval. (c) Check your result in part (b) by graphing / S
> Evaluate the integral. | tan'x sec'x dx
> Evaluate the integral. tan'x sec x dx
> Evaluate the integral. w/4 sec°0 tan°0 do
> Evaluate the integral. | tan'x sec'x dx
> Evaluate the integral. | (tan?x + tan“x) dx
> Evaluate the integral. ( tan?0 sec*0 do
> Evaluate the integral. tan x sec'x dx
> Evaluate the integral. |x sin'x dx
> Evaluate the integral. t sin't dt
> Evaluate the integral. sin x cos(r) dx
> Evaluate the integral. | cot x cos'x dx
> Evaluate the integral. sin°(1/t) dt
> Evaluate the integral. | Vcos 0 sin*0 do
> Evaluate the integral. "w/2 (2 – Jo sin 0)² d0
> Evaluate the integral. *w/2 sin'x cos?x dx Jo
> Evaluate the integral. (" sin?t cos*t dt
> Evaluate the integral. " cos“(21) dt
> Evaluate the integral. *2 sin°(40) do
> Evaluate the integral. '피/2 cos²0 d0 Jo
> Evaluate the integral. |t cos (1²) dt
> Evaluate the integral. sin (21) cos (21) dt

