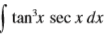Question: Evaluate the integral. /
> Find all functions f that satisfy the equation ) dx dx f(x) -1
> Let f be a function with the property that f(0) = 1, f’(0) = 1, and f(a+b) = f(a) f(b) for all real numbers a and b. Show that / for all x and deduce that /
> A student forgot the Product Rule for differentiation and made the mistake of thinking that / However, he was lucky and got the correct answer. The function f that he used was / and the domain of his problem was the interval / .What was the function t?
> Find all functions f such that f is continuous and [f(x)]² = 100 + * {[SM)² + [SOI*} dt for all real x
> Find all curves with the property that if a line is drawn from the origin to any point (x, y) on the curve, and then a tangent is drawn to the curve at that point and extended to meet the x-axis, the result is an isosceles triangle with equal sides meeti
> Find all curves with the property that if the normal line is drawn at any point P on the curve, then the part of the normal line between P and the x-axis is bisected by the y-axis.
> Evaluate the integral. Ste * dt
> Evaluate the integral. ,0.2y dy
> Evaluate the integral. Jx cos 5x dx
> Evaluate the integral using integration by parts with the indicated choices of u and dv. ( Vĩ In x dx; u = In x, dv = /x dx
> A finite Fourier series is given by the sum Show that the mth coefficient am is given by the formula N f(x) = E a, sin nx - a, sin x + a2 sin 2x + · · · + an sin Nx f(x) sin mx dx
> Prove the formula, where m and n are positive integers. 0if m+n п if m — п cos mx cos nx dx
> Prove the formula, where m and n are positive integers. So if m +n " sin mx sin nx dx T if m = n
> Prove the formula, where m and n are positive integers. T" sin mx cos nx dx = 0
> Household electricity is supplied in the form of alternating current that varies from 155 V to 2155 V with a frequency of 60 cycles per second (Hz). The voltage is thus given by the equation where t is the time in seconds. Voltmeters read the RMS (root-m
> Find the volume obtained by rotating the region bounded by the curves about the given axis. у — sec x, у — cos x, 0 <x< п/3; about y —-1
> Find the volume obtained by rotating the region bounded by the curves about the given axis. y = sin x, y = cos x, 0 < x </4; _about y 1
> Find the volume obtained by rotating the region bounded by the curves about the given axis. y = sin?x, y = 0, 0<x< ™; about the x-axis
> Use a graph of the integrand to guess the value of the integral. Then use the methods of this section to prove that your guess is correct. sin 27x cos 5T x dx Jo
> Use a graph of the integrand to guess the value of the integral. Then use the methods of this section to prove that your guess is correct. *2m cos'x dx Jo
> Find the area of the region bounded by the given curves. y tan x, y = tan?x, 0<x T/4
> Find the area of the region bounded by the given curves. y = sin?x, y = sin'x, 0<x< T
> Find the average value of the function f(x) = sin2x cos3x on the interval /
> Evaluate the indefinite integral. Illustrate, and check that your answer is reasonable, by graphing both the integrand and its antiderivative (taking C = 0). ( sec“(}x) dx
> Evaluate the indefinite integral. Illustrate, and check that your answer is reasonable, by graphing both the integrand and its antiderivative (taking C = 0). | sin 3x sin 6x dx
> Evaluate the indefinite integral. Illustrate, and check that your answer is reasonable, by graphing both the integrand and its antiderivative (taking C = 0). sin'x cos'x dx
> Prove the Root Test.
> Evaluate the indefinite integral. Illustrate, and check that your answer is reasonable, by graphing both the integrand and its antiderivative (taking C = 0). S x sin?(x²) dx
> Evaluate the integral. Sx tan'x dx
> Evaluate the integral. dx cos x - 1
> Evaluate the integral. *w/4 cos 40 de
> Evaluate the integral. *w/6 1 + cos 2x dx
> Evaluate the integral. *w/2 cos 5t cos 10t dt
> Evaluate the integral. sin 20 sin 60 do
> Evaluate the integral. | sin 8x cos 5x dx
> Evaluate the integral. w/3 csc'x dx Ju/6 (
> Use the sum of the first 10 terms to approximate the sum of the series Use Exercise 46 to estimate the error. Data from Exercise 46: Let / be a series with positive terms and let / Suppose that / converges by the Ratio Test. As usual, we let Rn be the
> Evaluate the integral. csc x dx
> Evaluate the integral. "w/2 csc*0 cot*0 d0 a/4
> Evaluate the integral. *w/2 " cot°o csc'p dp Jm/4
> Evaluate the integral. *w/2 cot'x dx /4
> Evaluate the integral. sin cos'o
> Evaluate the integral. sec x tan x dx
> Evaluate the integral. | tan?x sec x dx
> Evaluate the integral. ( tan'x dx
> Evaluate the integral. w/4 tan't dt
> Evaluate the integral. | dx tan'x sec"x
> (a) Approximate f by a Taylor polynomial with degree n at the number a. (b) Use Taylor’s Inequality to estimate the accuracy of the approximation / when x lies in the given interval. (c) Check your result in part (b) by graphing / S
> Evaluate the integral. | tan'x sec'x dx
> Evaluate the integral. w/4 sec°0 tan°0 do
> Evaluate the integral. | tan'x sec'x dx
> Evaluate the integral. | (tan?x + tan“x) dx
> Evaluate the integral. ( tan?0 sec*0 do
> Evaluate the integral. tan x sec'x dx
> Evaluate the integral. |x sin'x dx
> Evaluate the integral. t sin't dt
> Evaluate the integral. sin x cos(r) dx
> Evaluate the integral. | cot x cos'x dx
> Evaluate the integral. sin°(1/t) dt
> Evaluate the integral. | Vcos 0 sin*0 do
> Evaluate the integral. "w/2 (2 – Jo sin 0)² d0
> Evaluate the integral. *w/2 sin'x cos?x dx Jo
> Evaluate the integral. (" sin?t cos*t dt
> Evaluate the integral. " cos“(21) dt
> Evaluate the integral. *2 sin°(40) do
> Evaluate the integral. '피/2 cos²0 d0 Jo
> Evaluate the integral. |t cos (1²) dt
> Evaluate the integral. sin (21) cos (21) dt
> Evaluate the integral. *w/2 ( sin'x dx
> Evaluate the integral. *w/2 sin'0 cos*0 d0
> Evaluate the integral. sin*0 cos“0 d0
> Evaluate the integral. sin?x cos'x dx
> A water storage tank has the shape of a cylinder with diameter 10 ft. It is mounted so that the circular cross-sections are vertical. If the depth of the water is 7 ft, what per cent age of the total capacity is being used?
> Find the area of the crescent-shaped region (called a lune) bounded by arcs of circles with radii r and R. R
> A charged rod of length L produces an electric field at point P(a, b) given by where / is the charge density per unit length on the rod and «0 is the free space permittivity (see the figure). Evaluate the integral to determine an expression
> A torus is generated by rotating the circle x2 + (y-R)2 = r2 about the x-axis. Find the volume enclosed by the torus.
> The parabola y = 1 2 x2 divides the disk x2+y2 < 8 into two parts. Find the areas of both parts.
> For which positive integers k is the following series convergent? (n!)? Σ (kn)! 12 一1
> (a) Use trigonometric substitution to verify that (b) Use the figure to give trigonometric interpretations of both terms on the right side of the equation in part (a). Va? – 1? dt = }a² sin '(x/a) + £x /a? – x² y y=Va² -r
> Find the volume of the solid obtained by rotating about the line x = 1 the region under the curve /
> Find the volume of the solid obtained by rotating about the x-axis the region enclosed by the curves /
> Evaluate the integral Graph the integrand and its indefinite integral on the same screen and check that your answer is reasonable. dx x* /x? – 2
> Find the area of the region bounded by the hyperbola 9x2 - 4y2 = 36 and the line x = 3.
> Evaluate (a) by trigonometric substitution. (b) by the hyperbolic substitution x = a sinh t. x2 (x² + a²)½ dx
> (a) Use trigonometric substitution to show that (b) Use the hyperbolic substitution x = a sinh t to show that These formulas are connected by Formula 3.11.3. dx = In(x + Vx? + a²) + C x² + a² -2 (). dx sinh + C x² + a² a
> Evaluate the integral. cos t = dt V1 + sin?t */2 Jo
> For which of the following series is the Ratio Test inconclusive (that is, it fails to give a definite answer)? (a) 2 (b) E 2" (-3)*-1 (c) E Vn (d) E n-1 1 + n? n-1 2 - |
> Evaluate the integral. JxVī - x* dx
> Evaluate the integral. x? + 1 (x² – 2x + 2)
> Evaluate the integral. S | Vx? + 2x dx
> Evaluate the integral. - dx J (3 + 4x – 4x²)³/2
> Evaluate the integral. x² V3 + 2x – x² dx
> Evaluate the integral. x² dx
> Evaluate the integral. dx Vx? + 2x + 5
> Evaluate the integral. I Vx? + 1 dx
> Evaluate the integral. x2 r0.6 dx V9 - 25х?
> Evaluate the integral. dx V1 + x?
> Evaluate the integral. V1 + x? dx
> Evaluate the integral. dx I [(ax)? – b²]³/2
> Evaluate the integral. dx (2/3 JAs x/9x? – 1 J2/3