Question: Use the sum of the first 10
Use the sum of the first 10 terms to approximate the sum of the series
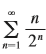
Use Exercise 46 to estimate the error.
Data from Exercise 46:
Let / be a series with positive terms and let / Suppose that / converges by the Ratio Test. As usual, we let Rn be the remainder after n terms, that is,

(a) If / is a decreasing sequence and / show, by summing a geometric series, that
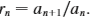
(b) If / is an increasing sequence, show that
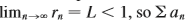
Transcribed Image Text:
2" Ea, = an+1/an. lim, >~ Γ =L< 1, so Σ a, 8.
> Use the Ratio Test to determine whether the series is convergent or divergent. n 100 100" Σ n!
> Use the Ratio Test to determine whether the series is convergent or divergent. の n!
> Use the information from Exercise 5 to estimate cos 80° correct to five decimal places. Data from Exercise 5: Find the Taylor polynomial T3(x) for the function f centered at the number a. Graph f and T3 on the same screen. f(x) cos х, a
> Use the Ratio Test to determine whether the series is convergent or divergent. cos(nп/3) n!
> Use the Ratio Test to determine whether the series is convergent or divergent. 10 (-10)**1 n+1 n-1
> Use the Ratio Test to determine whether the series is convergent or divergent. nT" Σ (-3)ª-| R-1
> Use the Ratio Test to determine whether the series is convergent or divergent. 10" Σ (п + 1)42я1 R-1
> Use the Ratio Test to determine whether the series is convergent or divergent. E ke * k-1
> Evaluate the integral. |x cosh ax dx
> Use the Ratio Test to determine whether the series is convergent or divergent. 00 k= k!
> Calculate 20 or 30 terms of the sequence for p0 = 1 2 and for two values of k such that 1 < k < 3. Graph each sequence. Do the sequences appear to converge? Repeat for a different value of p0 between 0 and 1. Does the limit depend on the choice of p0?
> A sub tangent is a portion of the x-axis that lies directly beneath the segment of a tangent line from the point of contact to the x-axis. Find the curves that pass through the point (c, 1) and whose sub tangents all have length c.
> Find the curve y = f(x) such that f(x) > 0, f(0) − 0, f(1) = 1, and the area under the graph off from 0 to x is proportional to the (n + 1)st power of f(x).
> Find all functions f that satisfy the equation ) dx dx f(x) -1
> Let f be a function with the property that f(0) = 1, f’(0) = 1, and f(a+b) = f(a) f(b) for all real numbers a and b. Show that / for all x and deduce that /
> A student forgot the Product Rule for differentiation and made the mistake of thinking that / However, he was lucky and got the correct answer. The function f that he used was / and the domain of his problem was the interval / .What was the function t?
> Find all functions f such that f is continuous and [f(x)]² = 100 + * {[SM)² + [SOI*} dt for all real x
> Find all curves with the property that if a line is drawn from the origin to any point (x, y) on the curve, and then a tangent is drawn to the curve at that point and extended to meet the x-axis, the result is an isosceles triangle with equal sides meeti
> Find all curves with the property that if the normal line is drawn at any point P on the curve, then the part of the normal line between P and the x-axis is bisected by the y-axis.
> Evaluate the integral. Ste * dt
> Evaluate the integral. ,0.2y dy
> Evaluate the integral. Jx cos 5x dx
> Evaluate the integral using integration by parts with the indicated choices of u and dv. ( Vĩ In x dx; u = In x, dv = /x dx
> A finite Fourier series is given by the sum Show that the mth coefficient am is given by the formula N f(x) = E a, sin nx - a, sin x + a2 sin 2x + · · · + an sin Nx f(x) sin mx dx
> Prove the formula, where m and n are positive integers. 0if m+n п if m — п cos mx cos nx dx
> Prove the formula, where m and n are positive integers. So if m +n " sin mx sin nx dx T if m = n
> Prove the formula, where m and n are positive integers. T" sin mx cos nx dx = 0
> Household electricity is supplied in the form of alternating current that varies from 155 V to 2155 V with a frequency of 60 cycles per second (Hz). The voltage is thus given by the equation where t is the time in seconds. Voltmeters read the RMS (root-m
> Find the volume obtained by rotating the region bounded by the curves about the given axis. у — sec x, у — cos x, 0 <x< п/3; about y —-1
> Find the volume obtained by rotating the region bounded by the curves about the given axis. y = sin x, y = cos x, 0 < x </4; _about y 1
> Find the volume obtained by rotating the region bounded by the curves about the given axis. y = sin?x, y = 0, 0<x< ™; about the x-axis
> Use a graph of the integrand to guess the value of the integral. Then use the methods of this section to prove that your guess is correct. sin 27x cos 5T x dx Jo
> Use a graph of the integrand to guess the value of the integral. Then use the methods of this section to prove that your guess is correct. *2m cos'x dx Jo
> Find the area of the region bounded by the given curves. y tan x, y = tan?x, 0<x T/4
> Find the area of the region bounded by the given curves. y = sin?x, y = sin'x, 0<x< T
> Find the average value of the function f(x) = sin2x cos3x on the interval /
> Evaluate the indefinite integral. Illustrate, and check that your answer is reasonable, by graphing both the integrand and its antiderivative (taking C = 0). ( sec“(}x) dx
> Evaluate the indefinite integral. Illustrate, and check that your answer is reasonable, by graphing both the integrand and its antiderivative (taking C = 0). | sin 3x sin 6x dx
> Evaluate the indefinite integral. Illustrate, and check that your answer is reasonable, by graphing both the integrand and its antiderivative (taking C = 0). sin'x cos'x dx
> Prove the Root Test.
> Evaluate the indefinite integral. Illustrate, and check that your answer is reasonable, by graphing both the integrand and its antiderivative (taking C = 0). S x sin?(x²) dx
> Evaluate the integral. Sx tan'x dx
> Evaluate the integral. dx cos x - 1
> Evaluate the integral. *w/4 cos 40 de
> Evaluate the integral. *w/6 1 + cos 2x dx
> Evaluate the integral. *w/2 cos 5t cos 10t dt
> Evaluate the integral. sin 20 sin 60 do
> Evaluate the integral. | sin 8x cos 5x dx
> Evaluate the integral. w/3 csc'x dx Ju/6 (
> Evaluate the integral. csc x dx
> Evaluate the integral. "w/2 csc*0 cot*0 d0 a/4
> Evaluate the integral. *w/2 " cot°o csc'p dp Jm/4
> Evaluate the integral. *w/2 cot'x dx /4
> Evaluate the integral. sin cos'o
> Evaluate the integral. sec x tan x dx
> Evaluate the integral. | tan?x sec x dx
> Evaluate the integral. ( tan'x dx
> Evaluate the integral. w/4 tan't dt
> Evaluate the integral. | dx tan'x sec"x
> (a) Approximate f by a Taylor polynomial with degree n at the number a. (b) Use Taylor’s Inequality to estimate the accuracy of the approximation / when x lies in the given interval. (c) Check your result in part (b) by graphing / S
> Evaluate the integral. | tan'x sec'x dx
> Evaluate the integral. tan'x sec x dx
> Evaluate the integral. w/4 sec°0 tan°0 do
> Evaluate the integral. | tan'x sec'x dx
> Evaluate the integral. | (tan?x + tan“x) dx
> Evaluate the integral. ( tan?0 sec*0 do
> Evaluate the integral. tan x sec'x dx
> Evaluate the integral. |x sin'x dx
> Evaluate the integral. t sin't dt
> Evaluate the integral. sin x cos(r) dx
> Evaluate the integral. | cot x cos'x dx
> Evaluate the integral. sin°(1/t) dt
> Evaluate the integral. | Vcos 0 sin*0 do
> Evaluate the integral. "w/2 (2 – Jo sin 0)² d0
> Evaluate the integral. *w/2 sin'x cos?x dx Jo
> Evaluate the integral. (" sin?t cos*t dt
> Evaluate the integral. " cos“(21) dt
> Evaluate the integral. *2 sin°(40) do
> Evaluate the integral. '피/2 cos²0 d0 Jo
> Evaluate the integral. |t cos (1²) dt
> Evaluate the integral. sin (21) cos (21) dt
> Evaluate the integral. *w/2 ( sin'x dx
> Evaluate the integral. *w/2 sin'0 cos*0 d0
> Evaluate the integral. sin*0 cos“0 d0
> Evaluate the integral. sin?x cos'x dx
> A water storage tank has the shape of a cylinder with diameter 10 ft. It is mounted so that the circular cross-sections are vertical. If the depth of the water is 7 ft, what per cent age of the total capacity is being used?
> Find the area of the crescent-shaped region (called a lune) bounded by arcs of circles with radii r and R. R
> A charged rod of length L produces an electric field at point P(a, b) given by where / is the charge density per unit length on the rod and «0 is the free space permittivity (see the figure). Evaluate the integral to determine an expression
> A torus is generated by rotating the circle x2 + (y-R)2 = r2 about the x-axis. Find the volume enclosed by the torus.
> The parabola y = 1 2 x2 divides the disk x2+y2 < 8 into two parts. Find the areas of both parts.
> For which positive integers k is the following series convergent? (n!)? Σ (kn)! 12 一1
> (a) Use trigonometric substitution to verify that (b) Use the figure to give trigonometric interpretations of both terms on the right side of the equation in part (a). Va? – 1? dt = }a² sin '(x/a) + £x /a? – x² y y=Va² -r
> Find the volume of the solid obtained by rotating about the line x = 1 the region under the curve /
> Find the volume of the solid obtained by rotating about the x-axis the region enclosed by the curves /
> Evaluate the integral Graph the integrand and its indefinite integral on the same screen and check that your answer is reasonable. dx x* /x? – 2
> Find the area of the region bounded by the hyperbola 9x2 - 4y2 = 36 and the line x = 3.
> Evaluate (a) by trigonometric substitution. (b) by the hyperbolic substitution x = a sinh t. x2 (x² + a²)½ dx
> (a) Use trigonometric substitution to show that (b) Use the hyperbolic substitution x = a sinh t to show that These formulas are connected by Formula 3.11.3. dx = In(x + Vx? + a²) + C x² + a² -2 (). dx sinh + C x² + a² a
> Evaluate the integral. cos t = dt V1 + sin?t */2 Jo
> For which of the following series is the Ratio Test inconclusive (that is, it fails to give a definite answer)? (a) 2 (b) E 2" (-3)*-1 (c) E Vn (d) E n-1 1 + n? n-1 2 - |

