Question: Evaluate the integral / Graph the integrand and
Evaluate the integral
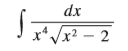
Graph the integrand and its indefinite integral on the same screen and check that your answer is reasonable.
Transcribed Image Text:
dx x* /x? – 2
> Evaluate the integral. sin 20 sin 60 do
> Evaluate the integral. | sin 8x cos 5x dx
> Evaluate the integral. w/3 csc'x dx Ju/6 (
> Use the sum of the first 10 terms to approximate the sum of the series Use Exercise 46 to estimate the error. Data from Exercise 46: Let / be a series with positive terms and let / Suppose that / converges by the Ratio Test. As usual, we let Rn be the
> Evaluate the integral. csc x dx
> Evaluate the integral. "w/2 csc*0 cot*0 d0 a/4
> Evaluate the integral. *w/2 " cot°o csc'p dp Jm/4
> Evaluate the integral. *w/2 cot'x dx /4
> Evaluate the integral. sin cos'o
> Evaluate the integral. sec x tan x dx
> Evaluate the integral. | tan?x sec x dx
> Evaluate the integral. ( tan'x dx
> Evaluate the integral. w/4 tan't dt
> Evaluate the integral. | dx tan'x sec"x
> (a) Approximate f by a Taylor polynomial with degree n at the number a. (b) Use Taylor’s Inequality to estimate the accuracy of the approximation / when x lies in the given interval. (c) Check your result in part (b) by graphing / S
> Evaluate the integral. | tan'x sec'x dx
> Evaluate the integral. tan'x sec x dx
> Evaluate the integral. w/4 sec°0 tan°0 do
> Evaluate the integral. | tan'x sec'x dx
> Evaluate the integral. | (tan?x + tan“x) dx
> Evaluate the integral. ( tan?0 sec*0 do
> Evaluate the integral. tan x sec'x dx
> Evaluate the integral. |x sin'x dx
> Evaluate the integral. t sin't dt
> Evaluate the integral. sin x cos(r) dx
> Evaluate the integral. | cot x cos'x dx
> Evaluate the integral. sin°(1/t) dt
> Evaluate the integral. | Vcos 0 sin*0 do
> Evaluate the integral. "w/2 (2 – Jo sin 0)² d0
> Evaluate the integral. *w/2 sin'x cos?x dx Jo
> Evaluate the integral. (" sin?t cos*t dt
> Evaluate the integral. " cos“(21) dt
> Evaluate the integral. *2 sin°(40) do
> Evaluate the integral. '피/2 cos²0 d0 Jo
> Evaluate the integral. |t cos (1²) dt
> Evaluate the integral. sin (21) cos (21) dt
> Evaluate the integral. *w/2 ( sin'x dx
> Evaluate the integral. *w/2 sin'0 cos*0 d0
> Evaluate the integral. sin*0 cos“0 d0
> Evaluate the integral. sin?x cos'x dx
> A water storage tank has the shape of a cylinder with diameter 10 ft. It is mounted so that the circular cross-sections are vertical. If the depth of the water is 7 ft, what per cent age of the total capacity is being used?
> Find the area of the crescent-shaped region (called a lune) bounded by arcs of circles with radii r and R. R
> A charged rod of length L produces an electric field at point P(a, b) given by where / is the charge density per unit length on the rod and «0 is the free space permittivity (see the figure). Evaluate the integral to determine an expression
> A torus is generated by rotating the circle x2 + (y-R)2 = r2 about the x-axis. Find the volume enclosed by the torus.
> The parabola y = 1 2 x2 divides the disk x2+y2 < 8 into two parts. Find the areas of both parts.
> For which positive integers k is the following series convergent? (n!)? Σ (kn)! 12 一1
> (a) Use trigonometric substitution to verify that (b) Use the figure to give trigonometric interpretations of both terms on the right side of the equation in part (a). Va? – 1? dt = }a² sin '(x/a) + £x /a? – x² y y=Va² -r
> Find the volume of the solid obtained by rotating about the line x = 1 the region under the curve /
> Find the volume of the solid obtained by rotating about the x-axis the region enclosed by the curves /
> Find the area of the region bounded by the hyperbola 9x2 - 4y2 = 36 and the line x = 3.
> Evaluate (a) by trigonometric substitution. (b) by the hyperbolic substitution x = a sinh t. x2 (x² + a²)½ dx
> (a) Use trigonometric substitution to show that (b) Use the hyperbolic substitution x = a sinh t to show that These formulas are connected by Formula 3.11.3. dx = In(x + Vx? + a²) + C x² + a² -2 (). dx sinh + C x² + a² a
> Evaluate the integral. cos t = dt V1 + sin?t */2 Jo
> For which of the following series is the Ratio Test inconclusive (that is, it fails to give a definite answer)? (a) 2 (b) E 2" (-3)*-1 (c) E Vn (d) E n-1 1 + n? n-1 2 - |
> Evaluate the integral. JxVī - x* dx
> Evaluate the integral. x? + 1 (x² – 2x + 2)
> Evaluate the integral. S | Vx? + 2x dx
> Evaluate the integral. - dx J (3 + 4x – 4x²)³/2
> Evaluate the integral. x² V3 + 2x – x² dx
> Evaluate the integral. x² dx
> Evaluate the integral. dx Vx? + 2x + 5
> Evaluate the integral. I Vx? + 1 dx
> Evaluate the integral. x2 r0.6 dx V9 - 25х?
> Evaluate the integral. dx V1 + x?
> Evaluate the integral. V1 + x? dx
> Evaluate the integral. dx I [(ax)? – b²]³/2
> Evaluate the integral. dx (2/3 JAs x/9x? – 1 J2/3
> Evaluate the integral. r Va² – x² dx
> Evaluate the integral. dx (x² + 1)?
> Evaluate the integral. Vx? – 9 dx 2 .3
> Evaluate the integral. dt V4 + t?
> Evaluate the integral. r1/2 x V1 – 4x² dx
> Evaluate the integral. 2/3 /4 - 9х? dx Jo
> Evaluate the integral. dx (x² 3/2
> Evaluate the integral. dt t?V12 – 16
> Evaluate the integral. dx Jo Ta² + x²)/2* a >0
> Evaluate the integral. dx (36— х2
> Evaluate the integral. .2 dx .4
> Evaluate the integral. x2 dx
> Evaluate the integral using the indicated trigonometric substitution. Sketch and label the associated right triangle. /x² – 4 dx X = 2 sec 0
> Evaluate the integral using the indicated trigonometric substitution. Sketch and label the associated right triangle. x x = 2 tan 0 dx Vx2 + 4
> Evaluate the integral using the indicated trigonometric substitution. Sketch and label the associated right triangle. dx x = 2 sin 0 J x4 - x2
> If a ≠0 and n is a positive integer, find the partial fraction decomposition of S(x) x"(х — а)
> If f is a quadratic function such that f(0) = 1 and is a rational function, find the value of f(0). f(x) ·dx x²(x + 1)'
> Suppose that F, G, and Q are polynomials and for all x except when Q(x) = 0. Prove that F(x) = G(x) for all x. F(x) G(x) Q(x) Q(x)
> (a) Use integration by parts to show that, for any positive integer n (b) Use part (a) to evaluate dx dx J (x² + a²)* 2a*(n – 1)(x² + a²)" -| 2n – 3 dx 2a*(n – 1) J 2а"(л — (x² + a²)ª ! dx dx and (x² + 1)² (x² + 1)'
> (a) Find the partial fraction decomposition of the function (b) Use part (a) to find / and graph f and its indefinite integral on the same screen. (c) Use the graph of f to discover the main features of the graph of / 12x – 7x – 13x² + 8 100x – 80x +
> (a) Use a computer algebra system to find the partial fraction decomposition of the function (b) Use part (a) to find / (by hand) and compare with the result of using the CAS to integrate f directly. Comment on any discrepancy. 4x – 27x² + 5x – 32 f(
> Factor x4 + 1 as a difference of squares by first adding and subtracting the same quantity. Use this factorization to evaluate /
> One method of slowing the growth of an insect population without using pesticides is to introduce into the population a number of sterile males that mate with fertile females but produce no offspring. (The photo shows a screw-worm fly, the first pest eff
> Find the volume of the resulting solid if the region under the curve / is rotated about (a) the x-axis and (b) the y-axis.
> Find the area of the region under the given curve from 1 to 2. х2 + 1 y 3x – x?
> Find the area of the region under the given curve from 1 to 2. 1 y = x' + x
> Use the substitution to transform the integrand into a rational function of t and then evaluate the integral. 12 sin 2x dx w/2 Jo 2 + cos x
> Use the substitution to transform the integrand into a rational function of t and then evaluate the integral. /2 dx /3 1 + sin x – cos x
> Use the substitution to transform the integrand into a rational function of t and then evaluate the integral. 1 dx 3 sin x – 4 cos x
> Use the substitution to transform the integrand into a rational function of t and then evaluate the integral. dx 1 - cos x
> The German mathematician Karl Weierstrass (1815–1897) noticed that the substitution t = tan(x/2) will convert any rational function of sin x and cos x into an ordinary rational function of t. (a) If / sketch a right triangle or use trig
> Evaluate the integral by completing the square and using Formula 6. 2х + 1 dx 4x? + 12х — 7
> Evaluate the integral by completing the square and using Formula 6. dx x² – 2x

