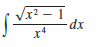Question: Use the substitution x = sec θ, where 0 < θ
> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. V4 + (In x)² dx
> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. x'e-* dx
> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. x*dx 10 – 2
> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. r/4x? – x* dx
> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. dx 3 - e2x
> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. sin 20 de 5 - sin 0
> For the function f whose graph is shown, list the following quantities in increasing order, from smallest to largest, and explain your reasoning. -2 5 (A) f f(x) dx (C) § f(x) dx (E) f'(1) (B) § f(x) dx (D) f(x) dx
> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. | sin'x cos x In(sin x) dx
> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. x sin(x?) cos(3x?) dx
> Let P be a pyramid with a square base of side 2b and suppose that is a sphere with its center on the base of P and S is tangent to all eight edges of P. Find the height of P. Then find the volume of the intersection of S and P.
> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. f v6 + 4y – 4y² dy
> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. ( sin-'VI dx
> Use the substitution u = tan x to evaluate the integral. n/4 tan'x sec'r dx
> Use the substitution u = sec x to evaluate the integral. ( tan'x sec'x dx
> Use the substitution u = sec x to evaluate the integral. | tan'x sec x dx
> Evaluate the integral. fπ/20 sin2x cos2x dx
> Evaluate the integral. f2π0 cos2 (6θ) dθ
> Evaluate the integral. f sin3 (mx) dx
> A wedge is cut out of a circular cylinder of radius 4 by two planes. One plane is perpendicular to the axis of the cylinder. The other intersects the first at an angle of 300 along a diameter of the cylinder. Find the volume of the wedge.
> Make a substitution to express the integrand as a rational function and then evaluate the integral. dx 2Vx + 3 + x
> A sphere of radius 1 overlaps a smaller sphere of radius in such a way that their intersection is a circle of radius r. (In other words, they intersect in a great circle of the small sphere.) Find r so that the volume inside the small sphere and outside
> Make a substitution to express the integrand as a rational function and then evaluate the integral. 16 x, -dx У9 х — 4
> Use long division to evaluate the integral. f10 x3 – 4x -10/ x2 – x – 6, dx
> Use long division to evaluate the integral. f x3 + 4/x2 + 4, dx
> Use long division to evaluate the integral. f r2/r + 4, dr
> Evaluate the integral. F3π/4π/2 sin5x cos3x dx
> Use long division to evaluate the integral. f x/x – 6, dx
> Evaluate the integral. f x2 – x + 6/ x3 + 3x, dx
> Evaluate the integral. f x3 + x2 + 2x + 1/ (x2 + 1) (x2 + 2), dx
> Evaluate the integral. f 2x2 + 5/ (x2 + 1) (x2 + 4), dx
> (a). Set up an integral for the volume of a solid torus (the donut-shaped solid shown in the figure) with radii r and R. (b). By interpreting the integral as an area, find the volume of the torus. -R-
> Water in an open bowl evaporates at a rate proportional to the area of the surface of the water. (This means that the rate of decrease of the volume is proportional to the area of the surface.) Show that the depth of the water decreases at a constant rat
> Some computer algebra systems have commands that will draw approximating rectangles and evaluate the sums of their areas, at least if is a left or right endpoint. (For instance, in Maple use leftbox, rightbox, leftsum, and rightsum.) (a). If f (x) = 1/ (
> First make a substitution and then use integration by parts to evaluate the integral. S cos Jī dx
> Evaluate the integral. f x2 + 2x – 1/ x3 – x, dx
> Evaluate the integral. f32 1/x2 – 1, dx
> Evaluate the integral. f10 x – 4/ x2 – 5x + 6, dx
> Evaluate the integral. f 5x + 1/ (2x + 1) (x – 1), dx
> Write out the form of the partial fraction expansion of the function. Do not determine the numerical values of the coefficients. x? (a) x? + x - 2 (b) x? + x + 2
> Evaluate the integral. fπ/20 cos5x dx
> Write out the form of the partial fraction expansion of the function. Do not determine the numerical values of the coefficients. 2x 1 (a) (x + 3)(3x + 1) (b) x' + 2x? + x
> Evaluate the integral. fx3/√x2 + 1, dx
> Archimedes’ Principle states that the buoyant force on an object partially or fully submerged in a fluid is equal to the weight of the fluid that the object displaces. Thus, for an object of density p0 floating partly submerged in a flu
> Evaluate the integral. f dx/x2√4 – x2
> Suppose that 0 < c < π/2. For what value of is the area of the region enclosed by the curves y = cos x, y = cos (x – c), and x = 0 equal to the area of the region enclosed by the curves y = cos (x – c), x = π, and y = 0?
> Evaluate the integral. f2√30 x3/√16 – x2, dx
> Evaluate the integral. f2√2 1/t3√t2 - 1
> (a). Verify, by differentiation, that f sec3θ dθ = 1/2 (sec θ tan θ+ ln |sec θ + tan θ|) + C (b). Evaluate f10 √x2 + 1, dx.
> Use the substitution x = 2 tan θ, -π/2 1 dx x'Vx? + 4
> Evaluate the integral. f arctan 4t dt
> Use the substitution u = tan x to evaluate the integral. tan'x secéx dx
> Evaluate the integral. f sin3x cos2x dx
> Suppose that for the tank in Exercise 19 the pump breaks down after 4.7 × 105 J of work has been done. What is the depth of the water remaining in the tank? Exercise 19: A tank is full of water. Find the work required to pump the water out
> Evaluate the integral. f ln 3√x dx
> Evaluate the integral. f x2 cos mx dx
> Find a positive continuous function f such that the area under the graph of f from 0 to t is A (t) = t3 for all t > 0.
> Evaluate the integral. f x2 sin πx dx
> Evaluate the integral. f t sin 2t dt
> Evaluate the integral. f rer/2 dr
> Evaluate the integral. f xe-x dx
> (a). Prove the reduction formula f cosnx dx = 1/n cosn-1 x sin x + n – 1/n f cosn-2x dx (b). Use part (a) to evaluate f cos2 x dx. (c). Use parts (a) and (b) to evaluate f cos4x dx.
> (a). Use the reduction formula in Example 6 to show that f sin2x x dx = x/2 – sin2x/4 + C. (b). Use part (a) and the reduction formula to evaluate f sin4x dx.
> Evaluate the indefinite integral. Illustrate, and check that your answer is reasonable, by graphing both the function and its antiderivative (take C = 0). (x? sin 2x dx
> (a). Show that the volume of a segment of height of a sphere of radius r is (See the figure.) (b). Show that if a sphere of radius 1 is sliced by a plane at a distance from the center in such a way that the volume of one segment is twice the volume of
> Evaluate the indefinite integral. Illustrate, and check that your answer is reasonable, by graphing both the function and its antiderivative (take C = 0). VI +x² dx
> Evaluate the indefinite integral. Illustrate, and check that your answer is reasonable, by graphing both the function and its antiderivative (take C = 0). x3/2 In x dx
> Evaluate the indefinite integral. Illustrate, and check that your answer is reasonable, by graphing both the function and its antiderivative (take C = 0).
> (a). Find the number such that the line x = a bisects the area under the curve y = 1/x2, 1 < x < 4. (b). Find the number such that the line y = b bisects the area in part (a).
> First make a substitution and then use integration by parts to evaluate the integral.
> Evaluate the integral. f x cox x dx
> First make a substitution and then use integration by parts to evaluate the integral.
> First make a substitution and then use integration by parts to evaluate the integral.
> First make a substitution and then use integration by parts to evaluate the integral.
> First make a substitution and then use integration by parts to evaluate the integral.
> (a). Graph several members of the family of functions f (x) = (2cx – x2)/c3 for c > 0 and look at the regions enclosed by these curves and the -axis. Make a conjecture about how the areas of these regions are related. (b). Prove your conjecture in part (
> Evaluate the integral. ft0 ex sin (t – s) ds
> Evaluate the integral. f21 (ln x)2 dx
> Evaluate the integral. f10 r3/√4 + r2, dr
> Evaluate the integral. f1/20 cos-1 x dx
> (a). If g (x)= (sin2x)/x2, use your calculator or computer to make a table of approximate values of ft1g (x) dx for t = 2, 5, 10, 100, 1000, and 10,000. Does it appear that f∞1g (x) dx is convergent? (b). Use the Comparison Theorem with f (x) = 1/x2 to s
> Evaluate the integral. F√31 arctan (1/x) dx
> Evaluate the integral using integration by parts with the indicated choices of u and dv.
> Evaluate the integral. f10 y/e2y dy
> Evaluate the integral. f94 ln y/√y dy
> Evaluate the integral. f21 ln x/x2 dx
> Three mathematics students have ordered a 14-inch pizza. Instead of slicing it in the traditional way, they decide to slice it by parallel cuts, as shown in the figure. Being mathematics majors, they are able to determine where to slice so that each gets
> Evaluate the integral. f10 (x2 + 1) e-x dx
> Evaluate the integral. fπ0 t sin 3t dt
> Evaluate the integral. f e-θ cos 2θ dθ
> Evaluate the integral. f e2θ sin 3θ dθ
> Evaluate the integral. f sin-1x dx
> Find the area of the region bounded by the parabola y = x2, the tangent line to this parabola at (1, 1) and the x-axis.
> Evaluate the integral. f p5 ln p dp
> Evaluate the integral using integration by parts with the indicated choices of u and dv.
> Evaluate the indefinite integral. f (3x – 2)20 dx
> Evaluate the indefinite integral. f x2 (x3 + 5)9 dx
> The Fresnel function S (x) = fx0sin (1/2Ï€t2) dt was introduced in Section 5.4. Fresnel also used the function in his theory of the diffraction of light waves. (a). On what intervals C is increasing? (b). On what intervals is C concave upward
> Evaluate the indefinite integral. f x sin (x2) dx
> Evaluate the integral by making the given substitution. f sec2(1/x)/x2 dx, u = 1/x
> Evaluate the integral by making the given substitution. f cos3θ sin θ d θ, u = cos θ