Question: Use the Table of Integrals on Reference
Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral.
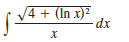
Transcribed Image Text:
V4 + (In x)² dx
> Estimate the area under the graph in the figure by using (a). the Trapezoidal Rule, (b). the Midpoint Rule, and (c). Simpson’s Rule, each with n = 6. у. 1 1 2 3 4 5 6 í
> Use a computer algebra system to evaluate the integral. Compare the answer with the result of using tables. If the answers are not the same, show that they are equivalent. |x*(1 + x')*dx
> A cow is tied to a silo with radius by a rope just long enough to reach the opposite side of the silo, as shown in the figure. Find the area available for grazing by the cow.
> Use a computer algebra system to evaluate the integral. Compare the answer with the result of using tables. If the answers are not the same, show that they are equivalent. sec" dx
> Verify Formula 31 (a) by differentiation and (b) by substituting u = a sin θ.
> Verify Formula 53 in the Table of Integrals (a) by differentiation and (b) by using the substitution t = a + bt.
> (a). Let R be the region that lies between two curves y = f (x) and y = g (x), where f (x) > g (x) and a (b). Find the centroid of the region bounded by the line y = x and the parabola y = x2. x[f(x) – g(x)] dx A A
> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. Se' sin(at – 3) dt
> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. Ver – I dx
> How large should n be to guarantee that the Simpson’s Rule approximation to f10ex2 dx is accurate to within 0.00001?
> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. | 20 sin 30 de
> (a). Find the approximations T10, M10, and S10 for fπ0 sin x dx and the corresponding errors Et, EM, and Es. (b). Compare the actual errors in part (a) with the error estimates given by (3) and (4). (c). How large do we have to choose so that the approxi
> (a). Find the approximations T10 and M10 for f21 e1/x dx. (b). Estimate the errors in the approximations of part (a). (c). How large do we have to choose so that the approximations Tn and Mn to the integral in part (a) are accurate to within 0.0001?
> Find a function f such that f (1) = -1, f (4) = 7, and f'(x) > 3 for all x, or prove that such a function cannot exist.
> (a). Find the approximations T8 and M8 for the integral f10 cos (x2) dx. (b). Estimate the errors in the approximations of part (a). (c). How large do we have to choose n so that the approximations Tn and Mn to the integral in part (a) are accurate to wi
> Use (a) the Trapezoidal Rule, (b) the Midpoint Rule, and (c) Simpson’s Rule to approximate the given integral with the specified value of n. (Round your answers to six decimal places.) Г In(x + 2) dx, п%3 10
> Use (a) the Trapezoidal Rule, (b) the Midpoint Rule, and (c) Simpson’s Rule to approximate the given integral with the specified value of n. (Round your answers to six decimal places.) cos x -dx, n= 8 rs
> Use (a) the Trapezoidal Rule, (b) the Midpoint Rule, and (c) Simpson’s Rule to approximate the given integral with the specified value of n. (Round your answers to six decimal places.) cos Vi dx, Vī dx, n = 10
> A bowl is shaped like a hemisphere with diameter 30 cm. A heavy ball with diameter 10 cm is placed in the bowl and water is poured into the bowl to a depth of h centimeters. Find the volume of water in the bowl.
> Use (a) the Trapezoidal Rule, (b) the Midpoint Rule, and (c) Simpson’s Rule to approximate the given integral with the specified value of n. (Round your answers to six decimal places.) sin t dt, n = 8
> Use (a) the Trapezoidal Rule, (b) the Midpoint Rule, and (c) Simpson’s Rule to approximate the given integral with the specified value of n. (Round your answers to six decimal places.) VI+ Vĩ dx, n= 8
> Use (a) the Trapezoidal Rule, (b) the Midpoint Rule, and (c) Simpson’s Rule to approximate the given integral with the specified value of n. (Round your answers to six decimal places.) *1/2 sin(e"2) dt, n= 8
> Use (a) the Trapezoidal Rule, (b) the Midpoint Rule, and (c) Simpson’s Rule to approximate the given integral with the specified value of n. (Round your answers to six decimal places.) dt n = 6 1+ t + t*'
> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. tan (1/2) -dz ,2
> A paper drinking cup filled with water has the shape of a cone with height and semi-vertical angle θ. (See the figure.) A ball is placed carefully in the cup, thereby displacing some of the water and making it overflow. What is the radius of
> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. dx 2x – 3x?
> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. x' sin x dx
> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. 2y² – 3 dy
> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. e2* arctan(e*) dx
> Use Exercise 40 to find f x4 ex dx. Exercise 40: f xn ex dx = xn ex – n f xn-1 ex dx
> Find the volume common to two spheres, each with radius r, if the center of each sphere lies on the surface of the other sphere.
> Use Exercise 39 to find f (ln x)3 dx. Exercise 39: f (ln x) n dx = x (ln x) n – n f (ln x) n-1 dx
> Prove that, for even powers of sine, 'm/2 1.3.5. . 3-5. (2n – 1) T sin2"x dx 2.4. 6. .... 2n 2
> (a). Use the reduction formula in Example 6 to show that fπ/20 sinnx dx = n – 1/n, fπ/20 sinn-2x dx where n > 2 is an integer. (b). Use part (a) to evaluate fπ/20 sin3x dx and fπ/20 sin5x d
> By completing the square in the quadratic 3 – 2x – x2 and making a trigonometric substitution, evaluate. dx V3 – 2x – x2
> If a, b, c, and d are constants such that find the value of the sum a + b + c + d. ax? + sin bx + sin cx + sin dx lim 8 3x? + 5x* + 7x6
> By completing the square in the quadratic x2 + x + 1 and making a substitution, evaluate dx x? + x+ 1
> Computer algebra systems sometimes need a helping hand from human beings. Try to evaluate f (1+ ln x) √1 + (x ln x)2, dx with a computer algebra system. If it doesn’t return an answer, make a substitution that changes the integral into one that the CAS c
> Use a computer algebra system to evaluate the integral. Compare the answer with the result of using tables. If the answers are not the same, show that they are equivalent. 1 dx VI +
> Use a computer algebra system to evaluate the integral. Compare the answer with the result of using tables. If the answers are not the same, show that they are equivalent. tan'x dx
> Use a computer algebra system to evaluate the integral. Compare the answer with the result of using tables. If the answers are not the same, show that they are equivalent. | sin'x dx
> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. dx x/4x2 + 9
> Let In = fπ/20 sinnx dx. (a). Show that I2n+2 (b). Use Exercise 38 to show that Exercise 38: Prove that, for even powers of sine, fπ/20 sin2nx dx = 1.3.5…. (2n – 1) π/ 2.4.6. . . 2n
> Use a computer algebra system to evaluate the integral. Compare the answer with the result of using tables. If the answers are not the same, show that they are equivalent. +2x хр
> Use a computer algebra system to evaluate the integral. Compare the answer with the result of using tables. If the answers are not the same, show that they are equivalent. dx Je-(3e* + 2)
> Use a computer algebra system to evaluate the integral. Compare the answer with the result of using tables. If the answers are not the same, show that they are equivalent. Sr Vx? + 4 dx
> The figure shows a semicircle with radius 1, horizontal diameter PQ, and tangent lines at P and Q. At what height above the diameter should the horizontal line be placed so as to minimize the shaded area? P.
> A tank is full of water. Find the work required to pump the water out of the spout. In Exercises 21 and 22 use the fact that water weighs 62.5 lb/ft3. 6 ft 8 ft -3 ft frustum of a cone
> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. sec?0 tan?0 de 9 – tan20
> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. x'e-* dx
> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. x*dx 10 – 2
> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. r/4x? – x* dx
> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. dx 3 - e2x
> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. sin 20 de 5 - sin 0
> For the function f whose graph is shown, list the following quantities in increasing order, from smallest to largest, and explain your reasoning. -2 5 (A) f f(x) dx (C) § f(x) dx (E) f'(1) (B) § f(x) dx (D) f(x) dx
> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. | sin'x cos x In(sin x) dx
> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. x sin(x?) cos(3x?) dx
> Let P be a pyramid with a square base of side 2b and suppose that is a sphere with its center on the base of P and S is tangent to all eight edges of P. Find the height of P. Then find the volume of the intersection of S and P.
> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. f v6 + 4y – 4y² dy
> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. ( sin-'VI dx
> Use the substitution u = tan x to evaluate the integral. n/4 tan'x sec'r dx
> Use the substitution u = sec x to evaluate the integral. ( tan'x sec'x dx
> Use the substitution u = sec x to evaluate the integral. | tan'x sec x dx
> Evaluate the integral. fπ/20 sin2x cos2x dx
> Evaluate the integral. f2π0 cos2 (6θ) dθ
> Evaluate the integral. f sin3 (mx) dx
> A wedge is cut out of a circular cylinder of radius 4 by two planes. One plane is perpendicular to the axis of the cylinder. The other intersects the first at an angle of 300 along a diameter of the cylinder. Find the volume of the wedge.
> Make a substitution to express the integrand as a rational function and then evaluate the integral. dx 2Vx + 3 + x
> A sphere of radius 1 overlaps a smaller sphere of radius in such a way that their intersection is a circle of radius r. (In other words, they intersect in a great circle of the small sphere.) Find r so that the volume inside the small sphere and outside
> Make a substitution to express the integrand as a rational function and then evaluate the integral. 16 x, -dx У9 х — 4
> Use long division to evaluate the integral. f10 x3 – 4x -10/ x2 – x – 6, dx
> Use long division to evaluate the integral. f x3 + 4/x2 + 4, dx
> Use long division to evaluate the integral. f r2/r + 4, dr
> Evaluate the integral. F3π/4π/2 sin5x cos3x dx
> Use long division to evaluate the integral. f x/x – 6, dx
> Evaluate the integral. f x2 – x + 6/ x3 + 3x, dx
> Evaluate the integral. f x3 + x2 + 2x + 1/ (x2 + 1) (x2 + 2), dx
> Evaluate the integral. f 2x2 + 5/ (x2 + 1) (x2 + 4), dx
> (a). Set up an integral for the volume of a solid torus (the donut-shaped solid shown in the figure) with radii r and R. (b). By interpreting the integral as an area, find the volume of the torus. -R-
> Water in an open bowl evaporates at a rate proportional to the area of the surface of the water. (This means that the rate of decrease of the volume is proportional to the area of the surface.) Show that the depth of the water decreases at a constant rat
> Some computer algebra systems have commands that will draw approximating rectangles and evaluate the sums of their areas, at least if is a left or right endpoint. (For instance, in Maple use leftbox, rightbox, leftsum, and rightsum.) (a). If f (x) = 1/ (
> First make a substitution and then use integration by parts to evaluate the integral. S cos Jī dx
> Evaluate the integral. f x2 + 2x – 1/ x3 – x, dx
> Evaluate the integral. f32 1/x2 – 1, dx
> Evaluate the integral. f10 x – 4/ x2 – 5x + 6, dx
> Evaluate the integral. f 5x + 1/ (2x + 1) (x – 1), dx
> Write out the form of the partial fraction expansion of the function. Do not determine the numerical values of the coefficients. x? (a) x? + x - 2 (b) x? + x + 2
> Evaluate the integral. fπ/20 cos5x dx
> Write out the form of the partial fraction expansion of the function. Do not determine the numerical values of the coefficients. 2x 1 (a) (x + 3)(3x + 1) (b) x' + 2x? + x
> Evaluate the integral. fx3/√x2 + 1, dx
> Archimedes’ Principle states that the buoyant force on an object partially or fully submerged in a fluid is equal to the weight of the fluid that the object displaces. Thus, for an object of density p0 floating partly submerged in a flu
> Evaluate the integral. f dx/x2√4 – x2
> Suppose that 0 < c < π/2. For what value of is the area of the region enclosed by the curves y = cos x, y = cos (x – c), and x = 0 equal to the area of the region enclosed by the curves y = cos (x – c), x = π, and y = 0?
> Evaluate the integral. f2√30 x3/√16 – x2, dx
> Evaluate the integral. f2√2 1/t3√t2 - 1
> (a). Verify, by differentiation, that f sec3θ dθ = 1/2 (sec θ tan θ+ ln |sec θ + tan θ|) + C (b). Evaluate f10 √x2 + 1, dx.
> Use the substitution x = 2 tan θ, -π/2 1 dx x'Vx? + 4
> Use the substitution x = sec θ, where 0 :- 1 di
> Evaluate the integral. f arctan 4t dt
> Use the substitution u = tan x to evaluate the integral. tan'x secéx dx

