Question: Use the Table of Integrals on Reference
Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral.
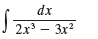
Transcribed Image Text:
dx 2x – 3x?
> If f (0) = g (0) = 0 and f" and g" are continuous, show that fWg"(x) dx = f(a)g'(a) – f'(a)gla) + {" f"()g(1) dx
> (a). Use integration by parts to show that f f (x) dx = xf (x) – f xf'(x) dx (b). If f and g are inverse functions and f' is continuous, prove that [Hint: Use part (a) and make the substitution y = f (x)] (c). In the case where f and
> Suppose that f (1) = 2, f (4) = 7, f'(1) = 5, f'(4) = 3, and f" is continuous. Find the value of f41 x f"(x) dx.
> A rocket accelerates by burning its onboard fuel, so its mass decreases with time. Suppose the initial mass of the rocket at liftoff (including its fuel) is m, the fuel is consumed at rate r, and the exhaust gases are ejected with constant velocity ve (r
> Solve Exercise 20 if the tank is half full of oil that has a density of 900 kg/m3. Exercise 20: A tank is full of water. Find the work required to pump the water out of the spout. In Exercises 21 and 22 use the fact that water weighs 62.5 lb/ft3.
> A particle that moves along a straight line has velocity v (t) = t2e-t meters per second after seconds. How far will it travel during the first seconds?
> Some of the pioneers of calculus, such as Kepler and Newton, were inspired by the problem of finding the volumes of wine barrels. (In fact, Kepler published a book Stereometria doliorum in 1615 devoted to methods for finding the volumes of barrels.) They
> Use integration by parts to prove the reduction formula. f xn ex dx = xn ex – n f xn-1 ex dx
> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. 1 dx x?/4x? – 7
> Use integration by parts to prove the reduction formula. f (ln x) n dx = x (ln x) n – n f (ln x) n-1 dx
> Use the Trapezoidal Rule with n = 10 to approximate f200 cos (πx) dx. Compare your result to the actual value. Can you explain the discrepancy?
> Sketch the graph of a continuous function on [0, 2] for which the Trapezoidal Rule with n = 2 is more accurate than the Midpoint Rule.
> Sketch the graph of a continuous function on [0, 2] for which the right endpoint approximation with n = 2 is more accurate than Simpson’s Rule.
> The intensity of light with wavelength traveling through a diffraction grating with N slits at an angle θ is given by I (θ) = N2 sin2k/k2, where k = (πNd sin θ)/λ and d is the distance between adjacent slits. A helium-neon laser with wavelength λ = 632.8
> The figure shows a pendulum with length L that makes a maximum angle θ0 with the vertical. Using Newton’s Second Law, it can be shown that the period T (the time for one complete swing) is given by where k = sin (1/2&Icir
> A uniform disk with radius 1 m is to be cut by a line so that the center of mass of the smaller piece lies halfway along a radius. How close to the center of the disk should the cut be made? (Express your answer correct to two decimal places.)
> (a). Use the table of integrals to evaluate F (x) = f f (x) dx, where f (x) = 1/x√1 – x2 What is the domain of f and F? (b). Use a CAS to evaluate F (x). What is the domain of the function F that the CAS produces? Is there a discrepancy between this doma
> Shown is the graph of traffic on an Internet service provider’s T1 data line from midnight to 8:00 AM. D is the data throughput, measured in megabits per second. Use Simpson’s Rule to estimate the total amount of data
> Let R be the region that lies between the curves y = xm and y = xn, 0 < x < 1, where m and n are integers with 0 < n < m. (a). Sketch the region R. (b). Find the coordinates of the centroid of R. (c). Try to find values of m and n such that the centroid
> The table (supplied by San Diego Gas and Electric) gives the power consumption P in megawatts in San Diego County from midnight to 6:00 AM on a day in December. Use Simpson’s Rule to estimate the energy used during that time period. (Us
> Water leaked from a tank at a rate of r (t) liters per hour, where the graph of is as shown. Use Simpson’s Rule to estimate the total amount of water that leaked out during the first 6 hours. 4 2 4 6 1 (seconds) 2.
> Estimate f10cos (x2) dx using (a) the Trapezoidal Rule and (b) the Midpoint Rule, each with n = 4. From a graph of the integrand, decide whether your answers are underestimates or overestimates. What can you conclude about the true value of the integral?
> The graph of the acceleration a (t) of a car measured in ft/s2 is shown. Use Simpson’s Rule to estimate the increase in the velocity of the car during the 6-second time interval. a. 12 8 4 6 t (seconds) 4)
> A radar gun was used to record the speed of a runner during the first 5 seconds of a race (see the table). Use Simpson’s Rule to estimate the distance the runner covered during those 5 seconds. t (s) v (m/s) t (s) v (m/s) 3.0 10.51
> Estimate the area under the graph in the figure by using (a). the Trapezoidal Rule, (b). the Midpoint Rule, and (c). Simpson’s Rule, each with n = 6. у. 1 1 2 3 4 5 6 í
> Use a computer algebra system to evaluate the integral. Compare the answer with the result of using tables. If the answers are not the same, show that they are equivalent. |x*(1 + x')*dx
> A cow is tied to a silo with radius by a rope just long enough to reach the opposite side of the silo, as shown in the figure. Find the area available for grazing by the cow.
> Use a computer algebra system to evaluate the integral. Compare the answer with the result of using tables. If the answers are not the same, show that they are equivalent. sec" dx
> Verify Formula 31 (a) by differentiation and (b) by substituting u = a sin θ.
> Verify Formula 53 in the Table of Integrals (a) by differentiation and (b) by using the substitution t = a + bt.
> (a). Let R be the region that lies between two curves y = f (x) and y = g (x), where f (x) > g (x) and a (b). Find the centroid of the region bounded by the line y = x and the parabola y = x2. x[f(x) – g(x)] dx A A
> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. Se' sin(at – 3) dt
> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. Ver – I dx
> How large should n be to guarantee that the Simpson’s Rule approximation to f10ex2 dx is accurate to within 0.00001?
> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. | 20 sin 30 de
> (a). Find the approximations T10, M10, and S10 for fπ0 sin x dx and the corresponding errors Et, EM, and Es. (b). Compare the actual errors in part (a) with the error estimates given by (3) and (4). (c). How large do we have to choose so that the approxi
> (a). Find the approximations T10 and M10 for f21 e1/x dx. (b). Estimate the errors in the approximations of part (a). (c). How large do we have to choose so that the approximations Tn and Mn to the integral in part (a) are accurate to within 0.0001?
> Find a function f such that f (1) = -1, f (4) = 7, and f'(x) > 3 for all x, or prove that such a function cannot exist.
> (a). Find the approximations T8 and M8 for the integral f10 cos (x2) dx. (b). Estimate the errors in the approximations of part (a). (c). How large do we have to choose n so that the approximations Tn and Mn to the integral in part (a) are accurate to wi
> Use (a) the Trapezoidal Rule, (b) the Midpoint Rule, and (c) Simpson’s Rule to approximate the given integral with the specified value of n. (Round your answers to six decimal places.) Г In(x + 2) dx, п%3 10
> Use (a) the Trapezoidal Rule, (b) the Midpoint Rule, and (c) Simpson’s Rule to approximate the given integral with the specified value of n. (Round your answers to six decimal places.) cos x -dx, n= 8 rs
> Use (a) the Trapezoidal Rule, (b) the Midpoint Rule, and (c) Simpson’s Rule to approximate the given integral with the specified value of n. (Round your answers to six decimal places.) cos Vi dx, Vī dx, n = 10
> A bowl is shaped like a hemisphere with diameter 30 cm. A heavy ball with diameter 10 cm is placed in the bowl and water is poured into the bowl to a depth of h centimeters. Find the volume of water in the bowl.
> Use (a) the Trapezoidal Rule, (b) the Midpoint Rule, and (c) Simpson’s Rule to approximate the given integral with the specified value of n. (Round your answers to six decimal places.) sin t dt, n = 8
> Use (a) the Trapezoidal Rule, (b) the Midpoint Rule, and (c) Simpson’s Rule to approximate the given integral with the specified value of n. (Round your answers to six decimal places.) VI+ Vĩ dx, n= 8
> Use (a) the Trapezoidal Rule, (b) the Midpoint Rule, and (c) Simpson’s Rule to approximate the given integral with the specified value of n. (Round your answers to six decimal places.) *1/2 sin(e"2) dt, n= 8
> Use (a) the Trapezoidal Rule, (b) the Midpoint Rule, and (c) Simpson’s Rule to approximate the given integral with the specified value of n. (Round your answers to six decimal places.) dt n = 6 1+ t + t*'
> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. tan (1/2) -dz ,2
> A paper drinking cup filled with water has the shape of a cone with height and semi-vertical angle θ. (See the figure.) A ball is placed carefully in the cup, thereby displacing some of the water and making it overflow. What is the radius of
> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. x' sin x dx
> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. 2y² – 3 dy
> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. e2* arctan(e*) dx
> Use Exercise 40 to find f x4 ex dx. Exercise 40: f xn ex dx = xn ex – n f xn-1 ex dx
> Find the volume common to two spheres, each with radius r, if the center of each sphere lies on the surface of the other sphere.
> Use Exercise 39 to find f (ln x)3 dx. Exercise 39: f (ln x) n dx = x (ln x) n – n f (ln x) n-1 dx
> Prove that, for even powers of sine, 'm/2 1.3.5. . 3-5. (2n – 1) T sin2"x dx 2.4. 6. .... 2n 2
> (a). Use the reduction formula in Example 6 to show that fπ/20 sinnx dx = n – 1/n, fπ/20 sinn-2x dx where n > 2 is an integer. (b). Use part (a) to evaluate fπ/20 sin3x dx and fπ/20 sin5x d
> By completing the square in the quadratic 3 – 2x – x2 and making a trigonometric substitution, evaluate. dx V3 – 2x – x2
> If a, b, c, and d are constants such that find the value of the sum a + b + c + d. ax? + sin bx + sin cx + sin dx lim 8 3x? + 5x* + 7x6
> By completing the square in the quadratic x2 + x + 1 and making a substitution, evaluate dx x? + x+ 1
> Computer algebra systems sometimes need a helping hand from human beings. Try to evaluate f (1+ ln x) √1 + (x ln x)2, dx with a computer algebra system. If it doesn’t return an answer, make a substitution that changes the integral into one that the CAS c
> Use a computer algebra system to evaluate the integral. Compare the answer with the result of using tables. If the answers are not the same, show that they are equivalent. 1 dx VI +
> Use a computer algebra system to evaluate the integral. Compare the answer with the result of using tables. If the answers are not the same, show that they are equivalent. tan'x dx
> Use a computer algebra system to evaluate the integral. Compare the answer with the result of using tables. If the answers are not the same, show that they are equivalent. | sin'x dx
> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. dx x/4x2 + 9
> Let In = fπ/20 sinnx dx. (a). Show that I2n+2 (b). Use Exercise 38 to show that Exercise 38: Prove that, for even powers of sine, fπ/20 sin2nx dx = 1.3.5…. (2n – 1) π/ 2.4.6. . . 2n
> Use a computer algebra system to evaluate the integral. Compare the answer with the result of using tables. If the answers are not the same, show that they are equivalent. +2x хр
> Use a computer algebra system to evaluate the integral. Compare the answer with the result of using tables. If the answers are not the same, show that they are equivalent. dx Je-(3e* + 2)
> Use a computer algebra system to evaluate the integral. Compare the answer with the result of using tables. If the answers are not the same, show that they are equivalent. Sr Vx? + 4 dx
> The figure shows a semicircle with radius 1, horizontal diameter PQ, and tangent lines at P and Q. At what height above the diameter should the horizontal line be placed so as to minimize the shaded area? P.
> A tank is full of water. Find the work required to pump the water out of the spout. In Exercises 21 and 22 use the fact that water weighs 62.5 lb/ft3. 6 ft 8 ft -3 ft frustum of a cone
> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. sec?0 tan?0 de 9 – tan20
> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. V4 + (In x)² dx
> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. x'e-* dx
> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. x*dx 10 – 2
> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. r/4x? – x* dx
> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. dx 3 - e2x
> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. sin 20 de 5 - sin 0
> For the function f whose graph is shown, list the following quantities in increasing order, from smallest to largest, and explain your reasoning. -2 5 (A) f f(x) dx (C) § f(x) dx (E) f'(1) (B) § f(x) dx (D) f(x) dx
> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. | sin'x cos x In(sin x) dx
> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. x sin(x?) cos(3x?) dx
> Let P be a pyramid with a square base of side 2b and suppose that is a sphere with its center on the base of P and S is tangent to all eight edges of P. Find the height of P. Then find the volume of the intersection of S and P.
> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. f v6 + 4y – 4y² dy
> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. ( sin-'VI dx
> Use the substitution u = tan x to evaluate the integral. n/4 tan'x sec'r dx
> Use the substitution u = sec x to evaluate the integral. ( tan'x sec'x dx
> Use the substitution u = sec x to evaluate the integral. | tan'x sec x dx
> Evaluate the integral. fπ/20 sin2x cos2x dx
> Evaluate the integral. f2π0 cos2 (6θ) dθ
> Evaluate the integral. f sin3 (mx) dx
> A wedge is cut out of a circular cylinder of radius 4 by two planes. One plane is perpendicular to the axis of the cylinder. The other intersects the first at an angle of 300 along a diameter of the cylinder. Find the volume of the wedge.
> Make a substitution to express the integrand as a rational function and then evaluate the integral. dx 2Vx + 3 + x
> A sphere of radius 1 overlaps a smaller sphere of radius in such a way that their intersection is a circle of radius r. (In other words, they intersect in a great circle of the small sphere.) Find r so that the volume inside the small sphere and outside
> Make a substitution to express the integrand as a rational function and then evaluate the integral. 16 x, -dx У9 х — 4
> Use long division to evaluate the integral. f10 x3 – 4x -10/ x2 – x – 6, dx
> Use long division to evaluate the integral. f x3 + 4/x2 + 4, dx
> Use long division to evaluate the integral. f r2/r + 4, dr
> Evaluate the integral. F3π/4π/2 sin5x cos3x dx
> Use long division to evaluate the integral. f x/x – 6, dx
> Evaluate the integral. f x2 – x + 6/ x3 + 3x, dx

