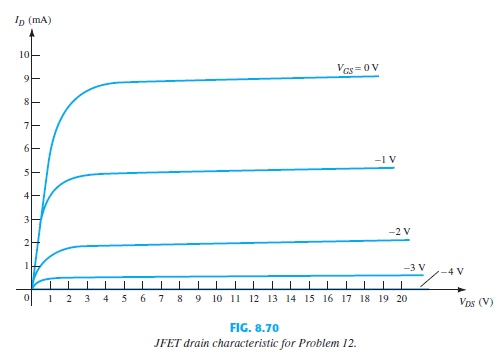
Question: Using the drain characteristic of Fig. 8.

> For the cascade amplifier of Fig. 8.94, calculate the dc bias voltages currents of each stage.

> For the cascade amplifier of Fig. 8.93, using JFETs with specifications IDSS = 12 mA, VP = - 3 V, and gos = 25 mS, calculate the circuit input impedance (Zi) and output impedance (Zo).

> If both JFETs in the cascade amplifier of Fig. 8.93 are changed to those having the specifications IDSS = 12 mA, VP = - 3 V, and gos = 25 mS, calculate the resulting voltage gain for each stage, the overall voltage gain, and the output voltage, Vo.

> If both JFETs in the cascade amplifier of Fig. 8.93 are changed to those having specifications IDSS = 12 mA and VP = - 3 V, calculate the resulting dc bias of each stage.

> For the JFET cascade amplifier of Fig. 8.93, using identical JFETs with IDSS = 8 mA and VP = - 4.5 V, calculate the voltage gain of each stage, the overall gain of the amplifier, and the output voltage Vo.

> For the JFET cascade amplifier in Fig. 8.93, calculate the dc bias conditions for the two identical stages, using JFETs with IDSS = 8 mA and VP = - 4.5 V.

> For a JFET having gm = 6 mS at VGSQ = - 1 V, what is the value of IDSS if VP = - 2.5 V?

> Design the self-bias network of Fig. 8.89 to have a gain of 10. The device should be biased at VGSQ= 1VP.

> Given the information appearing in Fig. 4.127, determine: a. IC. b. VE. c. VCC. d. VCE. e. VB. f. R1.

> Design the fixed-bias network of Fig. 8.88 to have a gain of 8.

> Determine the output voltage for the network of Fig. 8.87 if VI = 0.8 mV and rd = 40 kΩ.

> Determine Vo for the network of Fig. 8.86 if Vi = 4 mV, V GS (Th) = 4 V, and ID (on) = 4 mA, with VGS (on) = 7 V and gos = 20 mS.

> Determine VO for the network of Fig. 8.86 if VI = 20 mV.

> Repeat Problem 41 if k drops to 0.2 * 10-3. Compare results.

> Determine Zi, Zo, and Av for the amplifier of Fig. 8.85 if k = 0.3 * 10-3.

> Determine gm for a MOSFET if VGS (Th) = 3 V and it is biased at VGSQ = 8 V. Assume k = 0.3 * 10-3.

> Calculate the value of gm for a JFET (IDSS = 12 mA, VP = - 3 V) at a bias point of VGS = - 0.5 V.

> Determine Zi, Zo, and Av for the network of Fig. 8.84.

> Determine Vo for the network of Fig. 8.83 if Vi = 1.8 mV.

> Given the information provided in Fig. 4.126, determine: a. IC. b. VE. c. VB. d. R1.

> Repeat Problem 36 if rd = 25 kΩ and compare results.

> Determine Zi, Zo, and Av for the network of Fig. 8.82 if rd = 60 kΩ.

> Determine Vo for the network of Fig. 8.81 if gos = 20 mS.

> Determine Zi, Zo, and Av for the network of Fig. 8.80.

> Repeat Problem 32 if rd = 20 kΩ and compare results.

> Determine Zi, Zo, and Av for the network of Fig. 8.79.

> Determine Zi, Zo, and Av for the network of Fig. 8.78 if rd = 30 kΩ.

> Repeat Problem 29 if rd = 20 kΩ and compare results.

> For a JFET having device parameters gm0 = 5 mS and VP = - 4 V, what is the device current at VGS = 0 V?

> Determine Zi, Zo, and Vo for the network of Fig. 8.77 if Vi = 4 mV

> a. Repeat problem 15 for  = 140 using the general approach (not the approximate). b. What levels are affected the most? Why?

> Repeat Problem 26 if rd = 20 kΩ and compare results.

> Repeat Problem 25 if rd = 20 kΩ and compare results.

> Repeat Problem 25 with the capacitor CS removed and compare results.

> Determine Zi, Zo, and Vo for the network of Fig. 8.76 if Vi = 20 mV.

> Determine Zi, Zo, and Av for the network of Fig. 8.75 if IDSS = 6 mA, VP = - 6 V, and gos = 40 mS.

> a. Find the value of RS to obtain a voltage gain of 2 for the network of Fig. 8.74 using rd = ∞ Ω. b. Repeat part (a) with rd = 30 kΩ. What was the impact of the change in rd on the gain and the a

> Repeat Problem 20 if gos is 10 mS. Compare the results to those of Problem 20.

> Determine Zi, Zo, and Av for the network of Fig. 8.73 if the 20@mF capacitor is removed and the parameters of the network are the same as in Problem 20. Compare results with those of Problem 20.

> Determine Zi, Zo, and Av for the network of Fig. 8.73 if gfs = 3000 mS and gos = 50 ms.

> Determine the pinch-off voltage of a JFET with gm0 = 10 mS and IDSS = 12 mA.

> For the voltage-divider bias configuration of Fig. 4.125, determine: a. IBQ. b. ICQ. c. VCEQ. d. VC. e. VE. f. VB.

> a. Determine Zi, Zo, and Av for the network of Fig. 8.72 if IDSS = 10 mA, VP = —4 V, and rd = 20 kΩ. b. Repeat part (a) with rd = 40 kΩ. What was the impact on the results?

> a. Determine Zi, Zo, and Av for the network of Fig. 8.71 if IDSS and VP are one-half the values of Problems 17. This is IDSS = 5 mA and VP = —3 V. b. Compare the solutions to that of Problem 17.

> Determine Zi, Zo, and Av for the network of Fig. 8.71 if IDSS = 10 mA, VP = - 6 V, and rd = 40 kΩ.

> Sketch the ac equivalent model for a JFET if IDSS = 10 mA, VP = - 4 V, VGSQ = - 2 V, and gos = 25 mS.

> Sketch the ac equivalent model for a JFET if gfs = 5.6 mS and gos = 15 mS.

> a. Plot gm versus VGS for an n-channel JFET with IDSS = 12 mA and VP = - 6 V. b. Plot gm versus ID for the same n-channel JFET as part (a).

> For a 2N4220 n-channel JFET [gfs (minimum) = 750 mS, gos (maximum) = 10 mS]: a. What is the value of gm? b. What is the value of rd?

> Using the transfer characteristic of Fig. 8.69: a. What is the value of gm0? b. Determine gm at VGS = - 0.5 V graphically. c. What is the value of gm at VGSQ = - 0.5 V using Eq. (8.6)? Compare with the solution to part (b). d. Graphically determine gm at

> If a JFET having a specified value of rd = 100 kΩ has an ideal voltage gain of Av (FET) = - 200, what is the value of gm?

> For the network of Fig. 5.153, what value of RC will cut the voltage gain to half the value obtained in problem 13?

> Calculate gm0 for a JFET having device parameters IDSS = 12 mA and VP = - 4 V.

> Given the measurement VS = 1.7 V for the network of Fig. 7.82, determine: a. IDQ. b. VGSQ. c. IDSS. d. VD. e. VDS.

> For the network of Fig. 7.81, determine: a. VGSQ and IDQ. b. VDS, VD, VG, and VS.

> Determine IDQ for the network of Fig. 7.80 using a purely mathematical approach. That is, establish a quadratic equation for ID and choose the solution compatible with the network characteristics. Compare to the solution obtained in Problem 6.

> For the self-bias configuration of Fig. 7.80: a. Sketch the transfer curve for the device. b. Superimpose the network equation on the same graph. c. Determine IDQ and VGSQ. d. Calculate VDS, VD, VG, and VS.

> Determine VD and VGS for the fixed-bias configuration of Fig. 7.79.

> Determine VD and VGS for the fixed-bias configuration of Fig. 7.78.

> Repeat Problem 16 using the universal JFET bias curve.

> Repeat Problem 12 using the universal JFET bias curve.

> Repeat Problem 1 using the universal JFET bias curve.

> Using the characteristics of Fig. 4.121, determine the following for an emitter-bias configura- tion if a Q-point is defined at ICQ = 4 mA and VCEQ = 10 V. a. RC if VCC = 24 V and RE = 1.2 kΩ. b.  at the operating point. c. RB. d. Power dissipated by th

> For the network of Fig. 7.102, determine: a. IDQ and VGSQ. b. VDS. c. VD.

> For the network of Fig. 7.101, determine: a. IDQ and VGSQ. b. VDS. c. VD.

> The network of Fig. 7.100 is not operating properly. What is the specific cause for its failure?

> Although the readings of Fig. 7.99 initially suggest that the network is behaving properly, determine a possible cause for the undesirable state of the network.

> Given the measured value of VD in Fig. 7.77, determine: a. ID b. VDS c. VGG

> What do the readings for each configuration of Fig. 7.98 suggest about the operation of the network?

> Design a network such as appears in Fig. 7.39 using an enhancement-type MOSFET with PROBLEMS 479 VGS (Th) = 4 V and k = 0.5 * 10-3 A>V2 to have a Q-point of ID= 6 mA. Use a supply of 16 V and standard values.

> Design a voltage-divider bias network using a depletion-type MOSFET with IDSS = 10 mA and VP = - 4 V to have a Q-point at IDQ = 2.5 mA using a supply of 24 V. In addition, set VG = 4 V and use RD = 2.5RS with R1 = 22 MΩ. Use standard values.

> Design a self-bias network using a JFET transistor with IDSS = 8 mA and VP = - 6 V to have a Q-point at IDQ = 4 mA using a supply of 14 V. Assume that RD = 3RS and use standard values.

> For the combination network of Fig. 7.97, determine: a. VB and VG. b. VE. c. IE, IC, and ID. d. IB. e. VC, VS, and VD. f. VCE. g. VDS.

> Determine the saturation current (ICsat) for the network of Fig. 4.122.

> For the network of Fig. 7.96, determine: a. VG. b. VGSQ and IDQ. c. IE. d. IB. e. VD. f. VC.

> For the voltage-divider configuration of Fig. 7.95, determine: a. IDQ and VGSQ. b. VD and VS.

> For the network of Fig. 7.94, determine: a. IDQ. b. VGSQ and VDSQ. c. VD and VS. d. VDS.

> For the network of Fig. 7.93, determine: a. IDQ and VGSQ. b. VDS and VS.

> For the self-bias configuration of Fig. 7.92, determine: a. IDQ and VGSQ. b. VDS and VD.

> For the fixed-bias configuration of Fig. 7.76, determine: a. IDQ and VGSQ using a purely mathematical approach. b. Repeat part (a) using a graphical approach and compare results. c. Find VDS, VD, VG, and VS using the results of part (a).

> Determine VD and VGS for the network of Fig. 7.91 using the provided information.

> For the network of Fig. 7.90. a. Find IDQ. b. Determine VDQ and VDSQ. c. Find the power supplied by the source and dissipated by the device.

> Given VDS = 4 V for the network of Fig. 7.89, determine: a. ID. b. VD and VS. c. VGS.

> For the network of Fig. 7.88, determine: a. IDQ and VGSQ. b. VDS and VS.

> Given the information provided in Fig. 4.124, determine: a. . b. VCC. c. RB.

> Determine the value of RS for the network of Fig. 7.87 to establish VD = 10 V.

> For the network of Fig. 7.86, VD = 12 V. Determine: a. ID. b. VS and VDS. c. VG and VGS. d. VP.

> a. Repeat Problem 12 with RS = 0.51 kΩ (about 50% of the value of that of Problem 12). What is the effect of a smaller RS on IDQ and VGSQ? b. What is the minimum possible value of RS for the network of Fig. 7.85?

> For the network of Fig. 7.85, determine: a. VG. b. IDQ and VGSQ. c. VD and VS. d. VDSQ.

> Find VS for the network of Fig. 7.84.

> For the network of Fig. 7.83, determine: a. ID. b. VDS. c. VD. d. VS.

> For the fixed-bias configuration of Fig. 7.75: a. Sketch the transfer characteristics of the device. b. Superimpose the network equation on the same graph. c. Determine IDQ and VDSQ. d. Using Shockley’s equation, solve for IDQ and then

> In general, comment on the polarity of the various voltages and direction of the currents for an n-channel JFET versus a p-channel JFET.

> Given IDSS = 12 mA and  VP  = 6 V, sketch a probable distribution of characteristic curves for the JFET (similar to Fig. 6.11).

> a. Describe in your own words why IG is effectively  A for a JFET transistor. b. Why is the input impedance to a JFET so high? c. Why is the terminology field effect appropriate for this important three-terminal device?

> Given the characteristics of Fig. 6.54: a. Sketch the transfer characteristics directly from the drain characteristics. b. Using Fig. 6.54 to establish the values of IDSS and VP, sketch the transfer characteristics using Shockley’s equa

> a. Describe in your own words how the construction of the hot-carrier diode is significantly different from the conventional semiconductor diode. b. In addition, describe its mode of operation.

> Chief financial officers of U.S. companies were surveyed about areas in which job applicants make mistakes. Here are the areas and the frequency of responses: interview (452); resume (297); cover letter (141); reference checks (143); interview follow-up

> Listed below are the earnings (in millions of dollars) of the celebrities with the five highest incomes in a recent year. The celebrities in order are Steven Spielberg, Howard Stern, George Lucas, Oprah Winfrey, and Jerry Seinfeld. Can this “Top 5” list

> To find the mean wage of restaurant workers in the United States, an economist found the mean wage for each of the 50 states, and then calculated the mean of those 50 numbers.