Question: Write out the form of the partial
Write out the form of the partial fraction decomposition of the function (as in Example 7). Do not determine the numerical values of the coefficients.
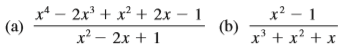
Transcribed Image Text:
x² – 1 x* – 2x + x? + 2x – 1 (a) (b) x³ + x + x x² – 2x + 1
> Make a substitution to express the integrand as a rational function and then evaluate the integral. e* (e* – 2)(e²* + 1) ,2x
> Make a substitution to express the integrand as a rational function and then evaluate the integral. sec?t -dt tan?t + 3 tan t + 2
> Make a substitution to express the integrand as a rational function and then evaluate the integral. sin x dx I cos'x – 3 cos x
> Make a substitution to express the integrand as a rational function and then evaluate the integral. ,2x e2х + Зе* + 2
> Make a substitution to express the integrand as a rational function and then evaluate the integral. dx
> Make a substitution to express the integrand as a rational function and then evaluate the integral. 1 - dx [Hint: Substitute u =
> Make a substitution to express the integrand as a rational function and then evaluate the integral. dx (1 + JF)²
> Show that the function is a solution of the differential equation S(x) = § (-1)*x 2n Σ (2n)! (-1)"x²" f"(x) + f(x) = 0
> (a) Approximate f by a Taylor polynomial with degree n at the number a. (b) Use Taylor’s Inequality to estimate the accuracy of the approximation / when x lies in the given interval. (c) Check your result in part (b) by graphing / S
> (a) Find the Taylor polynomials up to degree 3 for f(x) = tan x centered at a = 0. Graph f and these polynomials on a common screen. (b) Evaluate f and these polynomials at / and / (c) Comment on how the Taylor polynomials converge to f(x).
> Make a substitution to express the integrand as a rational function and then evaluate the integral. .3 Vx? dx + 1
> Make a substitution to express the integrand as a rational function and then evaluate the integral. 1 dx Jo 1+ x
> Make a substitution to express the integrand as a rational function and then evaluate the integral. dx x² + xF 2.
> Make a substitution to express the integrand as a rational function and then evaluate the integral. dx 2 Vx + 3 + x
> Make a substitution to express the integrand as a rational function and then evaluate the integral. dx x/x - 1
> Evaluate the integral. ' + 2x² + 3x – 2 dx (x² + 2x + 2)²
> Evaluate the integral. x? — Зх + 7 (x? — 4х + 6)?
> Evaluate the integral. x* + 3x? + 1 x* + 5x + 5x
> Evaluate the integral. 5x + 7x? + x + 2 dx x(x² + 1)²
> Evaluate the integral. x* + x – 1 x³ + 1
> Use the result of Example 7 to compute arctan 0.2 correct to five decimal places.
> Evaluate the integral. x' + 2x x* + 4x² + 3
> Evaluate the integral. dx x2 + 4x + 13 Jo
> Evaluate the integral. dx x³ – 1 3
> Evaluate the integral. x - 2x? + 2x – 5 dx x* + 4x² + 3
> Evaluate the integral. x + 4 dx J x? + 2x + 5
> Evaluate the integral. x3 + 6х — 2 dx x* + 6x²
> Evaluate the integral. x' + 4x + 3 dx x* + 5x? + 4
> Evaluate the integral. x? + x + 1 dx (x² + 1)²
> Evaluate the integral. 4x dx x² + x + 1 .3 x' +
> Evaluate the integral. x? - x + 6 dx x' + 3x
> Use a power series to approximate the definite integral to six decimal places. ro.3 dx 1+ x*
> Evaluate the integral. 10 dx (x – 1)(x² + 9) .2
> Evaluate the integral. x* + 9x? + x + 2 dx x² + 9
> Evaluate the integral. dt (1? – 1)?
> Evaluate the integral. x(3 — 5х) dx J (3x – 1)(x – 1)²
> Evaluate the integral. x? 1 + x + dx Jo (x + 1)°(x + 2)
> Evaluate the integral. Зx2 + 6х + 2 dx х? + 3х + 2
> Evaluate the integral. 4y? — Ту — 12 dy Л у(у + 2)(у — 3)
> Evaluate the integral. x' + 4x? + x - 1 dx x' + x?
> Evaluate the integral. x - 4x + 1 · dx 1 x² – 3x + 2
> Evaluate the integral. 1 (x + a)(x + b)
> Use a power series to approximate the definite integral to six decimal places. c0.2 x In(1 + x²) dx
> Evaluate the integral. x - 4 dx -o?? - 5x + 6
> Evaluate the integral. 2 dx Jo 2x + 3x + 1
> Evaluate the integral. y dy (y + 4)(2y – 1)
> Evaluate the integral. 5х + 1 - dx (2х + 1)(х — 1)
> Write out the form of the partial fraction decomposition of the function (as in Example 7). Do not determine the numerical values of the coefficients. 16 + 1 (a) 16 + t³ x* + 1 (b) (x² – x)(x* + 2x² + 1)
> Write out the form of the partial fraction decomposition of the function (as in Example 7). Do not determine the numerical values of the coefficients. (a) x? – 4 (b) (x² – x + 1)(x² + 2)²
> Write out the form of the partial fraction decomposition of the function (as in Example 7). Do not determine the numerical values of the coefficients. x' +1 (b) x³ – 3x² + 2x 1 (a) x? + x*
> Write out the form of the partial fraction decomposition of the function (as in Example 7). Do not determine the numerical values of the coefficients. х — 6 (a) x² + x – 6 x? (b) x? + x + 6
> Write out the form of the partial fraction decomposition of the function (as in Example 7). Do not determine the numerical values of the coefficients. 4 + x 1- x (a) (1 + 2х)(3 — х) (b) x' + x*
> Use a power series to approximate the definite integral to six decimal places. 1/2 " arctan(x/2) dx
> The functions y = ex2 and y = x2 ex2 don’t have elementary antiderivatives, but / does. Evaluate /
> Evaluate the integral. sin x cos x sin'x + cos“x
> Evaluate the integral. – sin x dx
> Evaluate the integral. sec x cos 2x sin x + sec x
> Evaluate the integral. Sx sin'x cos x dx
> Evaluate the integral. 1+ sin x dx SI 1- sin x
> Evaluate the integral. xe* dx /1 + e*
> Evaluate the integral. dx Vx² + 1
> Evaluate the integral. dx х In x — х
> Use a power series to approximate the definite integral to six decimal places. r0.3 Jo 1+ x3 dx
> Evaluate the integral. :+ arcsin. dx VI - x² 1 –
> Evaluate the integral. In(x + 1) ax x?
> Evaluate the integral. e 2x dx 1x 1+ e*
> Evaluate the integral. 1 dx 1+ 2e* — е *
> Evaluate the integral. 1 + x² dx 2
> Evaluate the integral. x? dx хв + 3x3 + 2
> Evaluate the integral. 1 dx /x + 1 + Vx
> Evaluate the integral. m/3_In(tan x) – dx Ja/4 sin x cos x
> Evaluate the integral. sin 2x dx J1+ cos“x
> Evaluate the integral. -dx I + x^^ Vx + 1
> Evaluate the indefinite integral as a power series. What is the radius of convergence? tan x dx
> Evaluate the integral. dx
> Evaluate the integral. de 1 + cos?e
> Evaluate the integral. de 1 + cos 0
> Evaluate the integral. dx J x*/4x? – 1
> Evaluate the integral. dx x* - 16
> Evaluate the integral. x In x dx /x² 1
> Evaluate the integral. fxk + c dx
> Evaluate the integral. dx x^x + x^
> Evaluate the integral. dx x + x/r
> Evaluate the integral. | (x + sin x)² dx
> Evaluate the indefinite integral as a power series. What is the radius of convergence? |x? In(1 + x) dx
> Evaluate the integral. |x' sinh mx dx х* si
> Evaluate the integral. dx Jx(x* + 1)
> Evaluate the integral. 1 x/4x2 + 1
> Evaluate the integral. 1 dx J x?V4x + 1
> Evaluate the integral. 1 dx J x/4x + 1
> Evaluate the integral. x/2 - VI - x² dx
> Evaluate the integral. Sx(x – 1) *dx
> Evaluate the integral. (x – 1)e* dx .2 x
> Evaluate the integral. fx'e "dx
> Evaluate the integral. SVi+e" dx
> Evaluate the indefinite integral as a power series. What is the radius of convergence? i - 1+ t
> Evaluate the integral. dx 1 + x³
> Evaluate the integral. tan'x dx
> Evaluate the integral. |O tan'o do
> Evaluate the integral. | sin 6x cos 3x dx

