Question:
(a). We define the improper integral (over the entire plane R2)
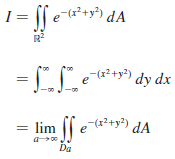
where Da is the disk with radius a and center the origin. Show that

(b). An equivalent definition of the improper integral in part (a) is
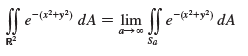
where Sa is the square with vertices (±a, ±a). Use this to show that
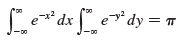
(c). Deduce that
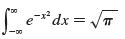
(d). By making the change of variable t = √2 x, show that
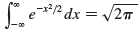
(This is a fundamental result for probability and statistics.)
Transcribed Image Text:
-(r²+y?) dA I = -(4²+y?) dy dx = lim | x²+y?) dA 2+3?) Da -(r²+y*) dA = -(r+y?) dA = lim a 00 R Sa e²dx dy = " e*dx = /m " e*? dx = V2 -x²/2
> Use cylindrical coordinates. Find the mass and center of mass of the solid S bounded by the paraboloid z = 4x2 + 4y2 and the plane z = a (a > 0) if S has constant density K.
> Use the Midpoint Rule for triple integrals (Exercise 24) to estimate the value of the integral. Divide B into eight sub-boxes of equal size. ∭B √x e xyz dV, where B = {(x, y, z) | 0 < x < 4, 0 < y < 1, 0 < z < 2} Exercise 24: (a). In the Midpoint Rule
> Use the Midpoint Rule for triple integrals (Exercise 24) to estimate the value of the integral. Divide B into eight sub-boxes of equal size. ∭B cos (xyz) dV, where B = {(x, y, z) | 0 < x < 1, 0 < y < 1, 0 < z < 1} Exercise 24: (a). In the Midpoint Rule
> Use cylindrical coordinates. Find the volume of the solid that lies between the paraboloid z = x2 + y2 and the sphere x2 + y2 + z2 = 2.
> Use cylindrical coordinates. Find the volume of the solid that is enclosed by the cone z = √(x^2 + y^2 ) and the sphere x2 + y2 + z2 = 2.
> Use cylindrical coordinates. Find the volume of the solid that lies within both the cylinder x2 + y2 = 1 and the sphere x2 + y2 + z2 = 4.
> Use cylindrical coordinates. Evaluate ∭E x2 dV, where E is the solid that lies within the cylinder x2 + y2 = 1, above the plane z = 0, and below the cone z2 = 4x2 + 4y2.
> Use cylindrical coordinates. Evaluate ∭E (x – y) dV, where E is the solid that lies between the cylinders x2 + y2 = 1 and x2 + y2 = 16, above the xy-plane, and below the plane z = y + 4.
> Plot the point whose cylindrical coordinates are given. Then find the rectangular coordinates of the point. (a). (√(2 ), 3π/4, 2) (b). (1, 1, 1)
> Use cylindrical coordinates. Evaluate ∭E (x + y + z) dV, where E is the solid in the first octant that lies under the paraboloid z = 4 - x2 - y2.
> Evaluate the integral where max {x2, y2} means the larger of the numbers x2 and y2. ,max(r".y") dy dx lo Jo
> Use cylindrical coordinates. Evaluate ∭E z dV, where E is enclosed by the paraboloid z = x2 + y2 and the plane z = 4.
> Use cylindrical coordinates. Evaluate ∭E √(x^2+ y^2 ) dV, where E is the region that lies inside the cylinder x2 + y2 = 16 and between the planes z = -5 and z = 4.
> Evaluate the triple integral. ∭E sin y dV, where E lies below the plane z = x and above the triangular region with vertices (0, 0, 0), (π, 0, 0), and (0, π, 0)
> Evaluate the triple integral. ∭E z/(x^2+y^2 ) dV, where E = {(x, y, z) | 1 < y < 4, y < z < 4, 0 < x < z j
> Evaluate the integral in Example 1, integrating first with respect to y, then z, and then x. Example 1: B = {(x, y, z) | 0 < x< 1, -1<y< 2, 0< z < 3}
> Evaluate the iterated integral. ∫_0^π ∫_0^1 ∫_0^(√(1-z^2 )) z sin x dy dz dx
> Sketch the solid whose volume is given by the iterated integral. ∫_0^2 ∫_0^(2-y) ∫_0^(4-y^2) dx dz dy
> Sketch the solid whose volume is given by the iterated integral. ∫_0^1 ∫_0^(1-x) ∫_0^(2-2z)〖dy dz dx〗
> (a). In the Midpoint Rule for triple integrals we use a triple Riemann sum to approximate a triple integral over a box B, where f (x, y, z) is evaluated at the center (x ̅i, y ̅j, z ̅k) of the box Bijk. Use the Midpoint Rule to estimate ∭B √(x^2 + y^2
> (a). Express the volume of the wedge in the first octant that is cut from the cylinder y2 1 z2 − 1 by the planes y = x and x = 1 as a triple integral. (b). Use either the Table of Integrals (on Reference Pages 6–10) or a computer algebra system to find t
> Evaluate lim┬(n→∞)n^(-2) ∑_(i=1)^n ∑_(j=1)^(n^2) 1/√(n^2+ni+j)
> Use a triple integral to find the volume of the given solid. The solid enclosed by the cylinder x2 + z2 = 4 and the planes y = -1 and y + z = 4
> Use a triple integral to find the volume of the given solid. The solid enclosed by the cylinder y = x2 and the planes z = 0 and y + z = 1
> Find, to four decimal places, the area of the part of the surface z = (1 + x2) / (1 + y2) that lies above the square |x | + |y | < 1. Illustrate by graphing this part of the surface.
> Evaluate the integral ∭E (xy + z2) dV, where E = {(x, y, z) | 0 < x < 2, 0 < y < 1, 0 < z < 36 using three different orders of integration.
> Find, to four decimal places, the area of the part of the surface z = 1 + x2y2 that lies above the disk x2 + y2 < 1.
> Evaluate the triple integral. ∭E z dV, where E is bounded by the cylinder y2 + z2 = 9 and the planes x = 0, y = 3x, and z = 0 in the first octant.
> Evaluate the triple integral. ∭E x dV, where E is bounded by the paraboloid x = 4y2 + 4z2 and the plane x = 4
> (a). Use the Midpoint Rule for double integrals with m = n = 2 to estimate the area of the surface z = xy + x2 + y2, 0 < x < 2, 0 < y < 2. (b). Use a computer algebra system to approximate the surface area in part (a) to four decimal places. Compare wit
> Find the area of the surface. The part of the surface z = xy that lies within the cylinder x2 + y2 = 1
> Find the area of the surface. The surface z =2/3 (x3/2 + y3/2), 0 < x < 1, 0 < y < 1
> If the ellipse x2/a2 + y2/b2 = 1 is to enclose the circle x2 + y2 = 2y, what values of a and b minimize the area of the ellipse?
> Find the area of the surface. The part of the hyperbolic paraboloid z = y2 - x2 that lies between the cylinders x2 + y2 = 1 and x2 + y2 = 4
> Find the area of the surface. The part of the cylinder x2 + z2 = 4 that lies above the square with vertices (0, 0), (1, 0), (0, 1), and (1, 1)
> Evaluate the integral by reversing the order of integration. ∫_0^2 ∫_(y/2)^1y cos (x3 – 1) dx dy
> Evaluate the integral by reversing the order of integration. ∫_0^1 ∫_(√x)^1√(y^3+1) dy dx
> Evaluate the integral by reversing the order of integration. ∫_0^1 ∫_(x^2)^1√y sin y dy dx
> Sketch the region of integration and change the order of integration. ∫_0^1 ∫_arctanx^(π/4) f (x,y) dy dx
> Find the mass and center of mass of the lamina that occupies the region D and has the given density function ρ. D is the triangular region with vertices (0, 0), (2, 1), (0, 3); ρ (x, y) = x + y
> Sketch the region of integration and change the order of integration. ∫_1^2 ∫_0^lnxf (x,y) dy dx
> Sketch the region of integration and change the order of integration. ∫_(-2)^2 ∫_0^(√(4-y^2 ) f (x,y) dx dy
> Sketch the region of integration and change the order of integration. ∫_0^(π/2) ∫_0^cosxf (x,y) dy dx
> Sketch the region of integration and change the order of integration. ∫_0^2 ∫_(x^2)^4 f (x,y) dy dx
> Sketch the region of integration and change the order of integration. ∫_0^1 ∫_0^y f (x,y) dx dy
> Calculate the iterated integral ∫(-3)^3 ∫_0^(π/2) (y+y^2 cos x ) dx dy
> Use a computer algebra system to find the exact volume of the solid. Enclosed by z = 1 - x2 - y2 and z = 0
> Use a computer algebra system to find the exact volume of the solid. Between the paraboloids z = 2x2 + y2 and z = 8 - x2 - 2y2 and inside the cylinder x2 + y2 = 1
> Use the result of Exercise 40 part (c) to evaluate the following integrals. Exercise 40 part (c): Deduce that (a). ∫_0^∞ x^2 e^(-x^2 ) dx (b). ∫_0^∞ √x e-x dx
> Find the area of the surface. The part of the surface 2y + 4z - x2 = 5 that lies above the triangle with vertices (0, 0), (2, 0), and (2, 4)
> Use polar coordinates to combine the sum into one double integral. Then evaluate the double integral. Sa l ty dy dx + ftvdy dx + 4-x2 xy dy dx ху.
> Calculate the iterated integral ∫_0^1 ∫_1^2(x+e^(-y) dx dy
> (a). Newton’s method for approximating a root of an equation f (x) = 0 (see Section 4.8) can be adapted to approximating a solution of a system of equations f (x, y) = 0 and g (x, y) = 0. The surfaces z = f (x, y) and z = t (x, y) inter
> Each of these extreme value problems has a solution with both a maximum value and a minimum value. Use Lagrange multipliers to find the extreme values of the function subject to the given constraint. f(x, y) %3 ху; 4х? + y? %3D 8 = 8
> Express the double integral in terms of a single integral with respect to r. Then use your calculator to evaluate the integral correct to four decimal places. ∬D e^(x^2+y^2 )^2 dA, where D is the disk with center the origin and radius 1
> Evaluate the iterated integral by converting to polar coordinates. ∫_0^2 ∫_0^(√(2x-x^2 ) √(x^2+y^2 ) dy dx
> Evaluate the iterated integral by converting to polar coordinates. ∫_0^(1/2) ∫_(√3 y)^(√(1-y^2 ) xy^2 dx dy
> Evaluate the iterated integral by converting to polar coordinates. ∫_0^a ∫_(-√(a^2-y^2 ))^(√(a^2-y^2 ) (2x + y) dx dy
> Find the mass and center of mass of the lamina that occupies the region D and has the given density function ρ. D = {(x, y) | 1 < x < 3, 1 < y < 4}; ρ (x, y) = ky2
> Evaluate the iterated integral by converting to polar coordinates. ∫_0^2 ∫_0^(√(4-x^2 ) e^(-x^2-y^2 ) dy dx
> Find the volume of the given solid. Bounded by the planes z = x, y = x, x + y = 2, and z = 0
> Use polar coordinates to find the volume of the given solid. Inside both the cylinder x2 + y2 = 4 and the ellipsoid 4x2 + 4y2 + z2 = 64
> Use a computer algebra system to find the mass, center of mass, and moments of inertia of the lamina that occupies the region D and has the given density function. D is enclosed by the right loop of the four-leaved rose r = cos 2θ; θ (x, y) = x2 + y2
> (a). Find the maximum value of f (x1, x2, . . . , xn) = √(n&x_1 x_2…x_n ) given that x1, x2, . . ., xn are positive numbers and x1 + x2 + ∙ ∙ ∙ + xn = c, wher
> If you attempt to use Formula 2 to find the area of the top half of the sphere x2 + y2 + z2 = a2, you have a slight problem because the double integral is improper. In fact, the integrand has an infinite discontinuity at every point of the boundary circl
> Show that the area of the part of the plane z = ax + by + c that projects onto a region D in the xy-plane with area A (D) is √(a^2 + b^2 + 1) A (D).
> Find the area of the surface. The part of the plane 6x + 4y + 2z = 1 that lies inside the cylinder x2 + y2 = 25
> Find the exact area of the surface z = 1 + x + y + x2 -2 < x < 1 -1 < y < 1 Illustrate by graphing the surface.
> Find the exact area of the surface z = 1 + 2x + 3y + 4y2, 1 < x < 4, 0 < y < 1.
> (a). Use the Midpoint Rule for double integrals (see Section 15.1) with four squares to estimate the surface area of the portion of the paraboloid z = x2 + y2 that lies above the square [0, 1] × [0, 1]. (b). Use a computer algebra system to approximate t
> Find the area of the surface correct to four decimal places by expressing the area in terms of a single integral and using your calculator to estimate the integral. The part of the surface z = cos (x2 + y2) that lies inside the cylinder x2 + y2 = 1
> Find the area of the surface correct to four decimal places by expressing the area in terms of a single integral and using your calculator to estimate the integral. The part of the surface z = 1/ (1 + x2 + y2) that lies above the disk x2 + y2 < 1
> Find the maximum and minimum values of f subject to the given constraints. Use a computer algebra system to solve the system of equations that arises in using Lagrange multipliers. (If your CAS finds only one solution, you may need to use additional comm
> Find the center of mass of the lamina in Exercise 11 if the density at any point is proportional to the square of its distance from the origin. Exercise 11: A lamina occupies the part of the disk x2 + y2 < 1 in the first quadrant. Find its center of ma
> Find the area of the surface. The part of the sphere x2 + y2 + z2 = a2 that lies within the cylinder x2 + y2 = ax and above the xy-plane
> Find the area of the surface. The part of the sphere x2 + y2 + z2 = 4 that lies above the plane z = 1
> Find the area of the surface. The part of the plane 5x + 3y = z + 6 = 0 that lies above the rectangle [1, 4] × [2, 6]
> Find the mass and center of mass of the lamina that occupies the region D and has the given density function ρ. D is bounded by the curves y = e-x, y = 0, x = 0, x = 1; ρ (x, y) = xy
> Find the mass and center of mass of the lamina that occupies the region D and has the given density function ρ. D is bounded by y = x + 2 and y = x2; ρ (x, y) = kx2
> Find the mass and center of mass of the lamina that occupies the region D and has the given density function ρ. D is bounded by y = 1 - x2 and y − 0; ρ (x, y) = ky
> Find the mass and center of mass of the lamina that occupies the region D and has the given density function ρ. D is the triangular region enclosed by the lines y = 0, y = 2x, and x + 2y = 1; ρ (x, y) = x
> Find the mass and center of mass of the lamina that occupies the region D and has the given density function ρ. D = {(x, y) | 0 < x < a, 0 < y < b}; ρ (x, y) = 1 + x2 + y2
> Find the maximum and minimum values of f subject to the given constraints. Use a computer algebra system to solve the system of equations that arises in using Lagrange multipliers. (If your CAS finds only one solution, you may need to use additional comm
> Use polar coordinates to find the volume of the given solid. Below the cone z = √(x^2 + y^2 ) and above the ring 1 < x2 + y2 < 4
> Electric charge is distributed over the disk x2 + y2 < 1 so that the charge density at (x, y) is (x, y) = √(x^2 + y^2 ) (measured in coulombs per square meter). Find the total charge on the disk.
> Use polar coordinates to find the volume of the given solid. Under the paraboloid z = x2 + y2 and above the disk x2 + y2 < 25
> Find the moments of inertia Ix, Iy, I0 for the lamina of Exercise 6. Exercise 6: Find the mass and center of mass of the lamina that occupies the region D and has the given density function ρ. D is the triangular region enclosed by the lines y = 0, y =
> Find the moments of inertia Ix, Iy, I0 for the lamina of Exercise 3. Exercise 3: Find the mass and center of mass of the lamina that occupies the region D and has the given density function ρ. D = {(x, y) | 1 < x < 3, 1 < y < 4}; ρ (x, y) = ky2
> A lamina occupies the region inside the circle x2 + y2 = 2y but outside the circle x2 + y2 = 1. Find the center of mass if the density at any point is inversely proportional to its distance from the origin.
> Find the center of mass of a lamina in the shape of an isosceles right triangle with equal sides of length a if the density at any point is proportional to the square of the distance from the vertex opposite the hypotenuse.
> Find the center of mass of the lamina in Exercise 13 if the density at any point is inversely proportional to its distance from the origin. Exercise 13: The boundary of a lamina consists of the semicircles y = √(1 - x^2 ) and y = √(4 - x^2 ) together w
> The boundary of a lamina consists of the semicircles y = √(1 - x^2 ) and y = √(4 - x^2 ) together with the portions of the x-axis that join them. Find the center of mass of the lamina if the density at any point is proportional to its distance from the o
> The plane 4x - 3y + 8z = 5 intersects the cone z2 = x2 + y2 in an ellipse. (a). Graph the cone and the plane, and observe the elliptical intersection. (b). Use Lagrange multipliers to find the highest and lowest points on the ellipse.
> A lamina occupies the part of the disk x2 + y2 < 1 in the first quadrant. Find its center of mass if the density at any point is proportional to its distance from the x-axis.
> Find the mass and center of mass of the lamina that occupies the region D and has the given density function ρ. D is enclosed by the curves y = 0 and y = cos x, -π/2 < x < π/2; ρ (x, y) = y
> Evaluate the given integral by changing to polar coordinates. ∬R sin (x2 + y2) dA, where R is the region in the first quadrant between the circles with center the origin and radii 1 and 3.
> Evaluate the given integral by changing to polar coordinates. ∬R (2x – y) dA, where R is the region in the first quadrant enclosed by the circle x2 + y2 = 4 and the lines x = 0 and y = x
> Evaluate the given integral by changing to polar coordinates. ∬D x2y dA, where D is the top half of the disk with center the origin and radius 5.
> Evaluate the iterated integral. ∫_0^1 ∫_0^(e^y) √(1+e^y) dw dv
> A region R is shown. Decide whether to use polar coordinates or rectangular coordinates and write∬R f (x, y) dA as an iterated integral, where f is an arbitrary continuous function on R. y. 3 х -3+

