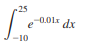[SOLVED] Evaluate the integrals in Problem. /

> Find the area bounded by the graphs of the indicated equations over the given intervals (when stated). Compute answers to three decimal places. [Hint: Area is always a positive quantity.]

> Refer to Figures A and B. Set up definite integrals that represent the indicated shaded areas over the given intervals. Referring to Figure A, explain how you would use definite integrals to find the area between the graph of y = ï¦(x)

> Refer to Figures A and B. Set up definite integrals that represent the indicated shaded areas over the given intervals. Over interval [b, d] in Figure B

> Refer to Figures A and B. Set up definite integrals that represent the indicated shaded areas over the given intervals. Over interval [a, b] in Figure B

> A chain of car muffler and brake repair shops maintains a training program for its mechanics. All new mechanics begin training in muffler repairs. Every 3 months, the performance of each mechanic is reviewed. Past records indicate that after each quarter

> Refer to Figures A and B. Set up definite integrals that represent the indicated shaded areas over the given intervals. Over interval [a, c] in Figure A

> Refer to Figures A and B. Set up definite integrals that represent the indicated shaded areas over the given intervals. Over interval [c, d] in Figure A

> Base your answers on the Gini index of income concentration(See Table 2) In which of Canada, Germany, or Japan is income most equally distributed? Most unequally distributed?

> Base your answers on the Gini index of income concentration(See Table 2) In which of China, India, or Iran is income most equally distributed? Most unequally distributed?

> Find the area bounded by the graphs of the indicated equations over the given interval. Compute answers to three decimal places.

> Refer to the matrices P and Q of Problem 59. For k a positive integer, let Tk = I + Q + Q2 + g+ Qk . (A) Explain why Tk + 1 = TkQ + I. (B) Using a graphing calculator and part (A) to quickly compute the matrices Tk, discover and describe the connectio

> Refer to Figures AâD. Set up definite integrals that represent the indicated shaded area. Explain why dx represents the area between the graph of y = h(x) and the x axis from x = a to x = b in Figure C.

> Use geometric formulas to find the unsigned area between the graph of y = ï¦(x) and the x axis over the indicated interval.

> The number of children in a large city was found to increase and then decrease rather drastically. If the number of children (in millions) over a 6-year period was given by what was the average number of children in the city over the 6-year period? [Ass

> A drug is injected into the bloodstream of a patient through her right arm. The drug concentration in the blood stream of the left arm t hours after the injection is given by What is the average drug concentration in the bloodstream of the left arm dur

> The rate at which the area of a skin wound is increasing is given (in square centimeters per day) by A′(t) = -0.9e-0.1t . The initial wound has an area of 9 square centimeters. How much will the area change during the first 5 days? The second 5 days?

> In Problem 87, if the rate is found to be then approximately how many barrels of oil will the field produce during the first 5 years of production? The second 5Â years of production?

> Repeat Problem 85 with an order of 1,200 units every 4Â months. What is the average number of units on hand for a 4-month period? Data from Problem 85: A store orders 600 units of a product every 3 months. If the product is steadily depleted

> If the rate of labor use in Problem 83 is then approximately how many labor-hours will be required to assemble the 9th through the 27th control units? [Hint: Let a = 8 and b = 27.]

> Given the demand function find the average price (in dollars) over the demand interval [400, 600].

> Show that S = [x 1 - x 0 0], 0 â¤ x â¤ 1, is a stationary matrix for the transition matrix Discuss the generalization of this result to any absorbing Markov chain with two absorbing states and two nonadsorb

> The rate at which the total amount of money put into an advertising campaign is changing is given by Aâ²(t) where t is the number of days since the campaign began. What does represent?

> The total cost (in dollars) of printing x dictionaries is C(x) = 20,000 + 10x. (A) Find the average cost per unit if 1,000 dictionaries are produced. (B) Find the average value of the cost function over the interval [0, 1,000]. (C) Discuss the differe

> The total accumulated costs C1t2 and revenues R1t2 (in thousands of dollars), respectively, for a coal mine satisfy C′(t) = 3 and R′(t) = 15e-0.1t where t is the number of years that the mine has been in operation. Find the useful life of the mine, to

> Refer to Problem 73. (A) Find a cubic regression equation for the data, and graph it and the data set in the same viewing window. (B) Use the regression equation and a numerical integration routine on a graphing calculator to approximate the number of

> Maintenance costs for an apartment house generally increase as the building gets older. From past records, the rate of increase in maintenance costs (in dollars per year) for a particular apartment complex is given approximately by where x is the age of

> Referring to Problem 69, compute the increase in cost going from a production level of 0 bikes per month to 600 bikes per month. Set up a definite integral and evaluate it. Data from Problem 69: A company manufactures mountain bikes. The research depart

> The fundamental theorem of calculus can be proved by showing that, for every positive integer n, there is a Riemann sum for f on [a, b] that is equal to F(b) â F(a). By the mean value theorem within each subinterval [xk - 1, xk] that be

> Use a numerical integration routine to evaluate each definite integral

> Evaluate the integrals.

> Verify the results in Problem 54 by computing Pk on a graphing calculator for large values of k.

> Evaluate the integrals.

> (A) Find the average value of each function over the indicated interval. (B) Use a graphing calculator to graph the function and its average value over the indicated interval in the same viewing window.

> Evaluate the integrals in Problem.

> Repeat Problem 53 for Data From Problem 53: Step 1 Using a transition diagram, rearrange the columns and rows of P to produce a standard form for this chain. Step 2 Find the limiting matrix for this standard form. Step 3 Using a transition diagram, rev

> Evaluate the integrals in Problem.

> Evaluate the integrals in Problem

> Evaluate the integrals in Problem.

> Use a graphing calculator to approximate the limiting matrix for the indicated standard form.

> Evaluate the integrals in Problem.

> (A) Calculate the change in F(x) from x = 10 to x = 15. (B) Graph F′(x) and use geometric formulas (see the endpapers at the back of the book) to calculate the area between the graph of F′(x) and the x axis from x = 10 to x = 15. (C) Verify that your a

> Use geometric formulas to find the unsigned area between the graph of y = ï¦(x) and the x axis over the indicated interval.

> Refer to the rectangles A, B, C, D, and E in the following figure. Which rectangles are both left and right rectangles?

> Refer to the rectangles A, B, C, D, and E in the following figure. Which rectangles are right rectangles?

> perform a mental calculation to find the answer and include the correct units. A square is circumscribed around a circle of radius 1 foot. Is the area inside the square but outside the circle less than 1 square foot?

> perform a mental calculation to find the answer and include the correct units. Find the total area enclosed by 5 non-overlapping rectangles, if each rectangle has width 3 feet and the heights of the rectangles are 2, 4, 6, 8, and 10 feet, respectively.

> Use a graphing calculator to approximate the limiting matrix for the indicated standard form.

> perform a mental calculation to find the answer and include the correct units. Find the total area enclosed by 6 non-overlapping rectangles, if each rectangle is 10 centimeters high and 3 centimeters wide.

> For the data in Problem 77, use left and right sums over three equal subintervals to approximate the area under the graph of Nâ²(x) from x = 0 to x = 6. Replace the question marks with values of L3 and R3 as appropriate: Data from Probl

> Refer to Problem 75. Use left and right sums over five equal subintervals to approximate the area under the graph of Aâ²(t) from t = 5 to t = 10. Calculate an error bound for this estimate. Data From Problem 75: The rate of healing, A&a

> For a new employee in Problem 73, use left and right sums to estimate the area under the graph of N(t) from t = 20 to t = 100. Use four equal subintervals for each. Replace the question marks with the values of L4 or R4 as appropriate:

> The left sum Ln or the right sum Rn is used to approximate the definite integral to the indicated accuracy. How large must n be chosen in each case? (Each function is increasing over the indicated interval.)

> the left sum Ln or the right sum Rn is used to approximate the definite integral to the indicated accuracy. How large must n be chosen in each case? (Each function is increasing over the indicated interval.)

> use derivatives to determine whether f is increasing or decreasing on the given interval. Use L4 or R4, whichever is appropriate, to give an overestimate of the signed area on the given interval.

> Use derivatives to determine whether ï¦ is increasing or decreasing on the given interval. Use L4 or R4, whichever is appropriate, to give an overestimate of the signed area on the given interval.

> Use L5 and R5 to approximate Compute error bounds for each. (Round answers to two decimal places.) Describe in geometric terms what the definite integral over the interval [1, 6] represents.

> Refer to the following figure showing two parcels of land along a river: Refer to Problem 61. Use R10 to estimate the combined areaÂ of both parcels, and calculate an error bound for this estimate. How many subdivisions of the baseline would

> discuss the validity of each statement. If the statement is always true, explain why. If not, give a counterexample. If a Markov chain is regular, then it is absorbing.

> could the given matrix be the transition matrix of an absorbing Markov chain?

> Discuss the validity of each statement. If the statement is always true, explain why. If it is not always true, give a counterexample. If ƒ is a decreasing function on [a, b], then the area under the graph of  is greater than the left sum Ln and less th

> Discuss the validity of each statement. If the statement is always true, explain why. If it is not always true, give a counterexample. If (x)= 2x on [0, 10] and n is a positive integer, then there is some Riemann sum Sn that equals the exact area under

> Discuss the validity of each statement. If the statement is always true, explain why. If it is not always true, give a counterexample.

> calculate the definite integral, given that

> calculate the definite integral by referring to the figure with the indicated areas.

> discuss the validity of each statement. If the statement is always true, explain why. If not, give a counterexample. If a Markov chain is absorbing, then it has a unique stationary matrix.

> calculate the definite integral by referring to the figure with the indicated areas.

Question: Evaluate the integrals in Problem. /