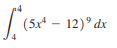[SOLVED] Evaluate the integrals in Problem /

> Refer to Figures A and B. Set up definite integrals that represent the indicated shaded areas over the given intervals. Over interval [b, d] in Figure B

> Refer to Figures A and B. Set up definite integrals that represent the indicated shaded areas over the given intervals. Over interval [a, b] in Figure B

> A chain of car muffler and brake repair shops maintains a training program for its mechanics. All new mechanics begin training in muffler repairs. Every 3 months, the performance of each mechanic is reviewed. Past records indicate that after each quarter

> Refer to Figures A and B. Set up definite integrals that represent the indicated shaded areas over the given intervals. Over interval [a, c] in Figure A

> Refer to Figures A and B. Set up definite integrals that represent the indicated shaded areas over the given intervals. Over interval [c, d] in Figure A

> Base your answers on the Gini index of income concentration(See Table 2) In which of Canada, Germany, or Japan is income most equally distributed? Most unequally distributed?

> Base your answers on the Gini index of income concentration(See Table 2) In which of China, India, or Iran is income most equally distributed? Most unequally distributed?

> Find the area bounded by the graphs of the indicated equations over the given interval. Compute answers to three decimal places.

> Refer to the matrices P and Q of Problem 59. For k a positive integer, let Tk = I + Q + Q2 + g+ Qk . (A) Explain why Tk + 1 = TkQ + I. (B) Using a graphing calculator and part (A) to quickly compute the matrices Tk, discover and describe the connectio

> Refer to Figures AâD. Set up definite integrals that represent the indicated shaded area. Explain why dx represents the area between the graph of y = h(x) and the x axis from x = a to x = b in Figure C.

> Use geometric formulas to find the unsigned area between the graph of y = ï¦(x) and the x axis over the indicated interval.

> The number of children in a large city was found to increase and then decrease rather drastically. If the number of children (in millions) over a 6-year period was given by what was the average number of children in the city over the 6-year period? [Ass

> A drug is injected into the bloodstream of a patient through her right arm. The drug concentration in the blood stream of the left arm t hours after the injection is given by What is the average drug concentration in the bloodstream of the left arm dur

> The rate at which the area of a skin wound is increasing is given (in square centimeters per day) by A′(t) = -0.9e-0.1t . The initial wound has an area of 9 square centimeters. How much will the area change during the first 5 days? The second 5 days?

> In Problem 87, if the rate is found to be then approximately how many barrels of oil will the field produce during the first 5 years of production? The second 5Â years of production?

> Repeat Problem 85 with an order of 1,200 units every 4Â months. What is the average number of units on hand for a 4-month period? Data from Problem 85: A store orders 600 units of a product every 3 months. If the product is steadily depleted

> If the rate of labor use in Problem 83 is then approximately how many labor-hours will be required to assemble the 9th through the 27th control units? [Hint: Let a = 8 and b = 27.]

> Given the demand function find the average price (in dollars) over the demand interval [400, 600].

> Show that S = [x 1 - x 0 0], 0 â¤ x â¤ 1, is a stationary matrix for the transition matrix Discuss the generalization of this result to any absorbing Markov chain with two absorbing states and two nonadsorb

> The rate at which the total amount of money put into an advertising campaign is changing is given by Aâ²(t) where t is the number of days since the campaign began. What does represent?

> The total cost (in dollars) of printing x dictionaries is C(x) = 20,000 + 10x. (A) Find the average cost per unit if 1,000 dictionaries are produced. (B) Find the average value of the cost function over the interval [0, 1,000]. (C) Discuss the differe

> The total accumulated costs C1t2 and revenues R1t2 (in thousands of dollars), respectively, for a coal mine satisfy C′(t) = 3 and R′(t) = 15e-0.1t where t is the number of years that the mine has been in operation. Find the useful life of the mine, to

> Refer to Problem 73. (A) Find a cubic regression equation for the data, and graph it and the data set in the same viewing window. (B) Use the regression equation and a numerical integration routine on a graphing calculator to approximate the number of

> Maintenance costs for an apartment house generally increase as the building gets older. From past records, the rate of increase in maintenance costs (in dollars per year) for a particular apartment complex is given approximately by where x is the age of

> Referring to Problem 69, compute the increase in cost going from a production level of 0 bikes per month to 600 bikes per month. Set up a definite integral and evaluate it. Data from Problem 69: A company manufactures mountain bikes. The research depart

> The fundamental theorem of calculus can be proved by showing that, for every positive integer n, there is a Riemann sum for f on [a, b] that is equal to F(b) â F(a). By the mean value theorem within each subinterval [xk - 1, xk] that be

> Use a numerical integration routine to evaluate each definite integral

> Evaluate the integrals.

> Verify the results in Problem 54 by computing Pk on a graphing calculator for large values of k.

> Evaluate the integrals.

> (A) Find the average value of each function over the indicated interval. (B) Use a graphing calculator to graph the function and its average value over the indicated interval in the same viewing window.

> Evaluate the integrals in Problem.

> Repeat Problem 53 for Data From Problem 53: Step 1 Using a transition diagram, rearrange the columns and rows of P to produce a standard form for this chain. Step 2 Find the limiting matrix for this standard form. Step 3 Using a transition diagram, rev

> Evaluate the integrals in Problem.

> Use a graphing calculator to approximate the limiting matrix for the indicated standard form.

> Evaluate the integrals in Problem.

> (A) Calculate the change in F(x) from x = 10 to x = 15. (B) Graph F′(x) and use geometric formulas (see the endpapers at the back of the book) to calculate the area between the graph of F′(x) and the x axis from x = 10 to x = 15. (C) Verify that your a

> Use geometric formulas to find the unsigned area between the graph of y = ï¦(x) and the x axis over the indicated interval.

> Refer to the rectangles A, B, C, D, and E in the following figure. Which rectangles are both left and right rectangles?

> Refer to the rectangles A, B, C, D, and E in the following figure. Which rectangles are right rectangles?

> perform a mental calculation to find the answer and include the correct units. A square is circumscribed around a circle of radius 1 foot. Is the area inside the square but outside the circle less than 1 square foot?

> perform a mental calculation to find the answer and include the correct units. Find the total area enclosed by 5 non-overlapping rectangles, if each rectangle has width 3 feet and the heights of the rectangles are 2, 4, 6, 8, and 10 feet, respectively.

> Use a graphing calculator to approximate the limiting matrix for the indicated standard form.

> perform a mental calculation to find the answer and include the correct units. Find the total area enclosed by 6 non-overlapping rectangles, if each rectangle is 10 centimeters high and 3 centimeters wide.

> For the data in Problem 77, use left and right sums over three equal subintervals to approximate the area under the graph of Nâ²(x) from x = 0 to x = 6. Replace the question marks with values of L3 and R3 as appropriate: Data from Probl

> Refer to Problem 75. Use left and right sums over five equal subintervals to approximate the area under the graph of Aâ²(t) from t = 5 to t = 10. Calculate an error bound for this estimate. Data From Problem 75: The rate of healing, A&a

> For a new employee in Problem 73, use left and right sums to estimate the area under the graph of N(t) from t = 20 to t = 100. Use four equal subintervals for each. Replace the question marks with the values of L4 or R4 as appropriate:

> The left sum Ln or the right sum Rn is used to approximate the definite integral to the indicated accuracy. How large must n be chosen in each case? (Each function is increasing over the indicated interval.)

> the left sum Ln or the right sum Rn is used to approximate the definite integral to the indicated accuracy. How large must n be chosen in each case? (Each function is increasing over the indicated interval.)

> use derivatives to determine whether f is increasing or decreasing on the given interval. Use L4 or R4, whichever is appropriate, to give an overestimate of the signed area on the given interval.

> Use derivatives to determine whether ï¦ is increasing or decreasing on the given interval. Use L4 or R4, whichever is appropriate, to give an overestimate of the signed area on the given interval.

> Use L5 and R5 to approximate Compute error bounds for each. (Round answers to two decimal places.) Describe in geometric terms what the definite integral over the interval [1, 6] represents.

> Refer to the following figure showing two parcels of land along a river: Refer to Problem 61. Use R10 to estimate the combined areaÂ of both parcels, and calculate an error bound for this estimate. How many subdivisions of the baseline would

> discuss the validity of each statement. If the statement is always true, explain why. If not, give a counterexample. If a Markov chain is regular, then it is absorbing.

> could the given matrix be the transition matrix of an absorbing Markov chain?

> Discuss the validity of each statement. If the statement is always true, explain why. If it is not always true, give a counterexample. If ƒ is a decreasing function on [a, b], then the area under the graph of  is greater than the left sum Ln and less th

> Discuss the validity of each statement. If the statement is always true, explain why. If it is not always true, give a counterexample. If (x)= 2x on [0, 10] and n is a positive integer, then there is some Riemann sum Sn that equals the exact area under

> Discuss the validity of each statement. If the statement is always true, explain why. If it is not always true, give a counterexample.

> calculate the definite integral, given that

> calculate the definite integral by referring to the figure with the indicated areas.

> discuss the validity of each statement. If the statement is always true, explain why. If not, give a counterexample. If a Markov chain is absorbing, then it has a unique stationary matrix.

> calculate the definite integral by referring to the figure with the indicated areas.

> calculate the indicated Riemann sum Sn for the function (x) = x2 - 5x - 6. Partition 31, 74 into six subintervals of equal length, and let c1 = 2, c2 = 2, c3 = 4, c4 = 4, c5 = 6, and c6 = 6.

> calculate the indicated Riemann sum Sn for the function (x) = x2 - 5x - 6. Partition 30, 34 into three subintervals of equal length, and let c1 = 0.2, c2 = 1.5, and c3 = 2.8.

> calculate the indicated Riemann sum Sn for the function (x) = 25 - 3x2 . Partition 3-5, 54 into five subintervals of equal length, and for each subinterval [xk - 1, xk], let ck = (xk - 1 + xk) /2.

> calculate the indicated Riemann sum Sn for the function (x) = 25 - 3x2 . Partition 30, 124 into four subintervals of equal length, and for each subinterval [xk - 1, xk], let ck = (xk - 1 + 2xk) /3.

Question: Evaluate the integrals in Problem /