Question: Evaluate the limit and justify each step
Evaluate the limit and justify each step by indicating the appropriate Limit Law(s).
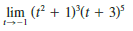
Transcribed Image Text:
lim (r + 1)'(t + 3)5 1--1
> The equation of motion of a particle is s = t3 – 3t, where s is in meters and is in seconds. Find (a). the velocity and acceleration as functions of t, (b). the acceleration after 2 s, and (c). the acceleration when the velocity is 0.
> Find the points on the curve where the tangent is horizontal or vertical. If you have a graphing device, graph the curve to check your work.
> Find the points on the curve where the tangent is horizontal or vertical. If you have a graphing device, graph the curve to check your work.
> Coffee is being poured into the mug shown in the figure at a constant rate (measured in volume per unit time). Sketch a rough graph of the depth of the coffee in the mug as a function of time. Account for the shape of the graph in terms of concavity. Wha
> Find an equation of the tangent line to the curve at the point corresponding to the given value of the parameter.
> Find an equation of the tangent line to the curve at the point corresponding to the given value of the parameter.
> Find an equation of the tangent line to the curve at the point corresponding to the given value of the parameter.
> Find equations of the tangent line and normal line to the curve at the given point. y = (1 + 2x)2 (1, 9)
> The flash unit on a camera operates by storing charge on a capacitor and releasing it suddenly when the flash is set off. The following data describe the charge Q remaining on the capacitor (measured in microcoulombs, µC) at time (measured i
> Air is being pumped into a spherical weather balloon. At any time t, the volume of the balloon is V (t) and its radius is r (t). (a). What do the derivatives dV/dr and dV/dt represent? (b). Express dV/dt in terms of dr/dt.
> A particle moves along a straight line with displacement s (t) velocity v (t), and acceleration a (t). Show that a (t) = v (t) = dv/ds Explain the difference between the meanings of the derivatives dv/dt and dv/ds.
> Under certain circumstances a rumor spreads according to the Equation P (t) = 1/1 + ae-kt where P (t) is the proportion of the population that knows the rumor at time t and a and k are positive constants. [In Section 7.5 we will see that this is a reason
> The motion of a spring that is subject to a frictional force or a damping force (such as a shock absorber in a car) is often modeled by the product of an exponential function and a sine or cosine function. Suppose the equation of motion of a point on suc
> In Example 4 in Section 1.3 we arrived at a model for the length of daylight (in hours) in Philadelphia on the tth day of the year: Use this model to compare how the number of hours of daylight is increasing in Philadelphia on March 21 and May 21.
> (a). Find the average rate of change of the area of a circle with respect to its radius r as r changes from (i). 2 to 3 (ii). 2 to 2.5 (iii). 2 to 2.1 (b). Find the instantaneous rate of change when r = 2. (c). Show that the rate of change of the area
> If x2 + xy + y3 = 1, find the value of y" at the point where x = 1.
> In the study of ecosystems, predator-prey models are often used to study the interaction between species. Consider populations of tundra wolves, given by W (t), and caribou, given by C (t), in northern Canada. The interaction has been modeled by the equa
> In a fish farm, a population of fish is introduced into a pond and harvested regularly. A model for the rate of change of the fish population is given by the equation where r0 is the birth rate of the fish, Pc is the maximum population that the pond can
> Refer to the law of laminar flow given in Example 7. Consider a blood vessel with radius 0.01 cm, length 3 cm, pressure difference 3000 dynes/cm2, and viscosity η = 0.027. (a). Find the velocity of the blood along the centerline r = 0, at radius r = 0.00
> Trace or copy the graph of the given function f. (Assume that the axes have equal scales.) Then use the method of Example 1 to sketch the graph of f' below it.
> Match the graph of each function in (a)–(d) with the graph of its derivative in I–IV. Give reasons for your choices.
> (a). The volume of a growing spherical cell is V = 4/3πr3, where the radius is measured in micrometers (1 µm = 10-6 m). Find the average rate of change of with respect to when changes from (i). 5 to 8 µm (ii). 5 to 6 µm (iii). 5 to 5.1 µm (b). Find the i
> A particle moves according to a law of motion s = f (t), t > 0, where is measured in seconds and in feet. (a). Find the velocity at time t. (b). What is the velocity after 3 s? (c). When is the particle at rest? (d). When is the particle moving in the po
> A particle moves according to a law of motion s = f (t), t > 0, where is measured in seconds and in feet. (a). Find the velocity at time t. (b). What is the velocity after 3 s? (c). When is the particle at rest? (d). When is the particle moving in the po
> If xy + ey = e, find the value of y" at the point where x = 0.
> (a). Sodium chlorate crystals are easy to grow in the shape of cubes by allowing a solution of water and sodium chlorate to evaporate slowly. If V is the volume of such a cube with side length x, calculate dV/dx when x = 3 mm and explain its meaning. (b)
> Let f (x) = 2x – tan x, -π/2 < x < π/2. On what interval is f concave downward?
> The graph of a function is shown in the figure. Make a rough sketch of an antiderivative F, given that F (0) = 1.
> The graph of a function f is shown. Which graph is an antiderivative of f and why?
> Shown is the graph of the population function P (t) for yeast cells in a laboratory culture. Use the method of Example 1 to graph the derivative P' (t). What does the graph of P' tell us about the yeast population?
> Find the derivative of the function. y = r/r2 + 1
> Suppose f'(x) = xe-x2. (a). On what interval is f increasing? On what interval is f decreasing? (b). Does f have a maximum value? Minimum value?
> Trace or copy the graph of the given function f. (Assume that the axes have equal scales.) Then use the method of Example 1 to sketch the graph of f' below it.
> Trace or copy the graph of the given function f. (Assume that the axes have equal scales.) Then use the method of Example 1 to sketch the graph of f' below it.
> Trace or copy the graph of the given function f. (Assume that the axes have equal scales.) Then use the method of Example 1 to sketch the graph of f' below it.
> Trace or copy the graph of the given function f. (Assume that the axes have equal scales.) Then use the method of Example 1 to sketch the graph of f' below it.
> (a). A company makes computer chips from square wafers of silicon. It wants to keep the side length of a wafer very close to 15 mm and it wants to know how the area A (x) of a wafer changes when the side length x changes. Find A'(15) and explain its mean
> The graph of the derivative f' of a continuous function f is shown. (a). On what intervals f is increasing? Decreasing? (b). At what values of x does f have a local maximum? Local minimum? (c). On what intervals is f concave upward? Concave downward? (
> Let K (t) be a measure of the knowledge you gain by studying for a test for t hours. Which do you think is larger, K (8) – K (7) or k (3) – K (2)? Is the graph of K concave upward or concave downward? Why?
> A particle is moving along a horizontal straight line. The graph of its position function (the distance to the right of a fixed point as a function of time) is shown. (a). When is the particle moving toward the right and when is it moving toward the le
> The table gives population densities for ring-necked pheasants (in number of pheasants per acre) on Pelee Island, Ontario. (a). Describe how the rate of change of population varies. (b). Estimate the inflection points of the graph. What is the signific
> A graph of a population of yeast cells in a new laboratory culture as a function of time is shown. (a). Describe how the rate of population increase varies. (b). When is this rate highest? (c). On what intervals is the population function concave upwar
> The graphs of a function f and its derivative f' are shown. Which is bigger, f' (-1) or f"(1)?
> Use the given graph of f to estimate the intervals on which the derivative f' is increasing or decreasing.
> The graph of the derivative f' of a function f is shown. (a). On what intervals is f increasing? Decreasing? (b). At what values of x does f have a local maximum? Local minimum? (c). If it is known that f (0) = 0, sketch a possible graph of f.
> The graph of the derivative f' of a function f is shown. (a). On what intervals is f increasing? Decreasing? (b). At what values of x does f have a local maximum? Local minimum? (c). If it is known that f (0) = 0, sketch a possible graph of f.
> (a). Find y' by implicit differentiation. (b). Solve the equation explicitly for and differentiate to get y' in terms of x. (c). Check that your solutions to parts (a) and (b) are consistent by substituting the expression for into your solution for part
> If a ball is thrown vertically upward with a velocity of 80 ft/s, then its height after seconds is s = 80t – 16t2. (a). What is the maximum height reached by the ball? (b). What is the velocity of the ball when it is 96 ft above the ground on its way up?
> The turkey in Example 1 is removed from the oven when its temperature reaches 1850F and is placed on a table in a room where the temperature is 750F. After 10 minutes the temperature of the turkey is and after 20 minutes it is 1600F. Use a linear approxi
> Let F (x) = x2 – 1/|x – 1|. (a) Find (i). limx→1+ F (x) (ii). limx→1- F (x) (b). Does limx→1 F (x) exist? (c). Sketch the graph of F.
> Find the limit, if it exists. If the limit does not exist, explain why. 2x + 12 lim I-6 |x + 6||
> Prove that limx→0+ √x esinπ/x = 0.
> If 2x < g (x) < x4 – x2 + 2 for all x, evaluate limx→1 g (x).
> If 4x – 9 < f (x) < x2 – 4x + 7 for x > 0, find limx→4 f (x).
> Use the Squeeze Theorem to show that limx→0 √x3 + x2 sin π/x = 0 Illustrate by graphing the functions f, g and h (in the notation of the Squeeze Theorem) on the same screen.
> (a). Estimate the value of limx→0 x/ 1 + 3x – 1 by graphing the function f (x) = x/ (√1 + 3x – 1). (b). Make a table of values of f (x) for x close to 0 and guess the value of the limit. (c). Use the Limit Laws to prove that your guess is correct.
> Evaluate the limit, if it exists. lim x → -4 √x2 + 9 – 5/ x + 4
> Evaluate the limit, if it exists. lim t → 0 (1/t√1 + t – 1/t)
> The point P (1, 0) lies on the curve y = sin (10π/x). (a). If Q is the point (x, sin (10π/x)), find the slope of the secant line PQ (correct to four decimal places) for x = 2, 1.5, 1.4, 1.3, 1.2, 1.1, 0.5, 0.6, 0.7, 0.8, and 0.9. Do the slopes appear to
> Evaluate the limit, if it exists. lim t → 0 (1/t – 1/t2 + t)
> Evaluate the limit, if it exists. lim x → 16 4 - √x / 16x – x2
> Evaluate the limit, if it exists. lim x → -1 x2 + 2x + 1/ x4 - 1
> Explain what it means to say that limx→1- = f (x) = 3 and limx→1+ = f (x) = 7 In this situation is it possible that limx→1 = f (x) = 5 exists? Explain.
> Evaluate the limit, if it exists. lim h → 0 √1 + h - 1/h
> Evaluate the limit, if it exists. lim x → 2 x + 2 / x3 + 8
> Evaluate the limit, if it exists. lim h → 0 (2 + h)3 – 8 / h
> Evaluate the limit, if it exists. lim x → -1 x2 – 4x / x2 – 3x - 4
> Evaluate the limit, if it exists. lim x → -3 t2 - 9 + 1/ 2x2 + 7t + 3
> Evaluate the limit, if it exists. lim x → -1 2x2 + 3x + 1/ x2 - 2x – 3
> (a). What is wrong with the following equation? x2 + x – 6/ x - 2 = x + 3 (b). In view of part (a), explain why the equation lim x →2 x2 + x - 6 x - 2 = lim x→2 (x + 3) is correct.
> Given that limx→2 f (x) = 4 limx→2 g (x) = -2 limx→2 h (x) = 0 find the limits that exist. If the limit does not exist, explain why. (a) lim [f(x) + 5g(x)] (b) lim [g(x)]° (c) lim F(x) 3f(x) (d)
> Use the graph of the function f to state the value of each limit, if it exists. If it does not exist, explain why. (a) lim f(x) (b) lim f(x) (c) lim f(x) 1 f(x): 1 + %3D
> Sketch the graph of the function and use it to determine the values of for which limx→a f (x) exists. (1+х if x << -1 f(x) = {x if –1<x<1 2 — х if x> 1
> If a rock is thrown upward on the planet Mars with a velocity of 10 m/s, its height in meters seconds later is given by y = 10t – 1.8t2 (a). Find the average velocity over the given time intervals: (i). [1, 2] (ii). [1, 1.5] (iii). [1, 1.1] (iv). [1, 1
> For the function whose graph is given, state the value of each quantity, if it exists. If it does not exist, explain why. 4- -2 2 4 す (a) lim g(t) (b) lim g(t) (c) lim g(t) (d) lim g(t) (e) lim g(t) (f) lim g(1) -2+ (g) g(2) (h) lim g(t)
> For the function f whose graph is given, state the value of each quantity, if it exists. If it does not exist, explain why. 4. 2- 4 2. (a) lim f(x) (b) lim f(x) (c) lim f(x) (d) lim f(x) (e) f(3)
> The displacement (in centimeters) of a particle moving back and forth along a straight line is given by the equation of motion s = 2 sin πt + 3 cos πt, where is measured in seconds. (a). Find the average velocity during each time period: (i). [1, 2] (ii
> The table shows the position of a cyclist. (a). Find the average velocity for each time period: (i). [1, 3] (ii). [2, 3] (iii). [3, 5] (iv). [3, 4] (b) Use the graph of as a function of to estimate the instantaneous velocity when t = 3. t (second
> If a ball is thrown into the air with a velocity of 40 ft/s, its height in feet seconds later is given by y = 40t – 16t2. (a). Find the average velocity for the time period beginning when t = 2 and lasting (i). 0.5 second (ii). 0.1 second (iii). 0.05 se
> The point P (0, 5, 0) lies on the curve y = cos πx. (a). If Q is the point (x, cos πx), use your calculator to find the slope of the secant line (correct to six decimal places) for the following values of x: (i). 0 (ii). 0.4 (iii). 0.49 (iv). 0.499 (v
> Find an equation of the tangent line to the curve at the given point. y = √x, (1, 1)
> A cardiac monitor is used to measure the heart rate of a patient after surgery. It compiles the number of heartbeats after t minutes. When the data in the table are graphed, the slope of the tangent line represents the heart rate in beats per minute. T
> If and are positive numbers, prove that the equation a/x3 + 2x2 – 1 + b/x3 + x – 2 = 0 has at least one solution in the interval (-1, 1).
> The figure shows a fixed circle C1 with equation (x -1)2 + y2 = 1 and a shrinking circle C2 with radius r and center the origin. P is the point (0, r), Q is the upper point of intersection of the two circles, and R is the point of intersection of the lin
> Find a formula for a function that has vertical asymptotes x = 1 and x = 3 and horizontal asymptote y = 1.
> Find a formula for a function that satisfies the following conditions: lim f(x) = 0, lim f(x) = -0, f(2) = 0, %3D lim f(x) = 0, lim f(x) = -0 %3D I-3+
> Use the Intermediate Value Theorem to show that there is a root of the given equation in the specified interval. ex = 3 – 2x, (0, 1)
> A Tibetan monk leaves the monastery at 7:00 AM and takes his usual path to the top of the mountain, arriving at 7:00 PM. The following morning, he starts at 7:00 AM at the top and takes the same path back, arriving at the monastery at 7:00 PM. Use the In
> Is there a number that is exactly 1 more than its cube?
> Is there a number a such that limx→2 3x2 +ax + a+ 3/x2 + x - 2 exists? If so, find the value of a and the value of the limit.
> (a) Prove that the equation has at least one real root. (b) Use your graphing device to find the root correct to three decimal places. √x - 5 = 1/x + 3
> For the function whose graph is given, state the value of each quantity, if it exists. If it does not exist, explain why. -4 -2 2 4 6 (a) lim h(x) (b) lim h(x) (c) lim h(x) --3- I--3+ --3 (d) h(-3) (e) lim h(x) (f) lim h(x) (g) lim h(x) (h) h(0) (i
> (a) Prove that the equation has at least one real root. (b) Use your graphing device to find the root correct to three decimal places. 100e-x/100 = 0.01x2
> (a). Prove that the equation has at least one real root. (b). Use your calculator to find an interval of length 0.01 that contains a root. ln x = 3 – 2x
> Use the Intermediate Value Theorem to show that there is a root of the given equation in the specified interval. x4 + x - 3 = 0 (1, 2)
> Let f (x) = [[cos x]], -Ï€ (a). Sketch the graph of (b). Evaluate each limit, if it exists. (c). For what values of a does limx→ a f (x) exist? (i) lim f(x) (ii) lịm f(x) I-(m/2)- (iii) lim f(x) 1-(m/2)+ (iv) lim f(x) 1/
> (a). A tank contains 5000 L of pure water. Brine that contains 30 g of salt per liter of water is pumped into the tank at a rate of 25 L/min. Show that the concentration of salt after t minutes (in grams per liter) is (b). What happens to the concentra
> (a). Show that the absolute value function F (x) = |x| is continuous everywhere. (b). Prove that if f is a continuous function on an interval, then so is |f|. (c). Is the converse of the statement in part (b) also true? In other words, if |f| is continuo
> Show that the function is continuous on (-∞, ∞). [x* sin(1/x) if x # 0 f(x) = if x= 0
> The graph shows the influence of the temperature T on the maximum sustainable swimming speed of Coho salmon. (a). What is the meaning of the derivative S'(T)? What are its units? (b). Estimate the values of S'(15) and S'(25) and interpret them. SA

