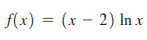[SOLVED] Find  (x) and find the equation of

> Find ï¦â²(x) and find the value(s) of x where the tangent line is horizontal.

> Find ï¦â²(x) and find the equation of the line tangent to the graph of ï¦ï at the indicated value of x.

> find the indicated derivative and simplify.

> A single card is drawn from a standard 52-card deck. Calculate the probability of each event. A king or a heart is drawn.

> find the indicated derivative and simplify.

> Find the indicated derivative and simplify.

> Find ï¦â²(x)and the equation of the line tangent to the graph of ï¦ at the indicated value of x. Find the value(s) of x where the tangent line is horizontal.

> Find ï¦â²(x) and simplify.

> An experiment consists of tossing three fair (not weighted) coins, except that one of the three coins has a head on both sides. Compute the probability of obtaining the indicated results. More than 1tail

> Find ï¦â²(x) and simplify.

> Replace ? with an expression that will make the indicated equation valid.

> Find (A) the derivative of T(x) / B(x) without using the quotient rule, and (B) Tâ²(x) / Bâ²(x). Note that the answer to part (B) is different from the answer to part (A).

> Use these frequencies to calculate the approximate empirical probabilities and odds for the events (A) The sum is a prime number or is exactly divisible by 4. (B) The sum is an odd number or exactly divisible by 3

> Exercises write the expression as a quotient of integers, reduced to lowest terms.

> Find (A) the derivative of F(x) S(x) without using the product rule, and (B) Fâ²(x) Sâ²(x). Note that the answer to part (B) is different from the answer to part (A)

> One hour after a dose of x milligrams of a particular drug is administered to a person, the change in body temperature T(x), in degrees Fahrenheit, is given approximately by The rate Tâ²(x) at which T changes with respect to the size of

> According to economic theory, the supply x of a quantity in a free market increases as the price p increases (see the figure). Suppose that the number x of DVD players a retail chain is willing to sell per week at a price of $p is given by (A) Find dx

> A communications company has installed a new cable television system in a city. The total number N (in thousands) of subscribers t months after the installation of the system is given by (A) Find Nâ²(t). (B) Find N(16) and Nâ&#1

> Find each indicated derivative and simplify.

> An experiment consists of tossing three fair (not weighted) coins, except those one of the three coins has a head on both sides. Compute the probability of obtaining the indicated results. 0 Heads

> Find each indicated derivative and simplify.

> Find ï¦â²(x) in two ways: (1) using the product or quotient rule and (2) simplifying first.

> Find ï¦â² (x) and find the value(s) of x where ï¦â² (x) = 0.

> Find ï¦ (x) and find the equation of the line tangent to the graph of ï¦ at x = 2.

> (A) What are the odds for rolling a sum of 10 in a single roll of two fair dice? (B) If you bet $1 that a sum of 10 will turn up, what should the house pay (plus returning your $1 bet) if a sum of 10 turns up in order for the game to be fair? A pair of

> Find ï¦ (x) and find the equation of the line tangent to the graph of ï¦ at x = 2.

> (A) Find ï¦(x) using the quotient rule, and (B) Explain how ï¦(x) can be found easily without using the quotient rule.

> Find the indicated derivatives and simplify.

> find the indicated derivatives and simplify.

> Find the indicated derivatives and simplify.

> Find hâ²(x), where ï¦(x) is an unspecified differentiable function.

> An experiment consists of tossing three fair (not weighted) coins, except those one of the three coins has a head on both sides. Compute the probability of obtaining the indicated results. 2 Heads

> Find hâ²(x), where ï¦(x) is an unspecified differentiable function.

> Find ï¦(x) and simplify.

> Compute the odds against obtaining. An odd number or a number divisible by 3 in a single roll of a die.

> Find ï¦(x) and simplify.

> Find (A) the derivative of T(x) / B(x) without using the quotient rule, and (B) Tâ²(x) / Bâ²(x). Note that the answer to part (B) is different from the answer to part (A).

> solve for the variable without using a calculator. ln x = 2

> solve for the variable without using a calculator. log10 x = -3

> An experiment consists of rolling two fair dice and adding the dots on the two sides facing up. Using the sample space shown in Figure 2 (page 398) and, assuming each simple event is as likely as any other, find the probability of the sum of the dots ind

> solve for the variable without using a calculator. y = log4 64

> An investment of $25,000 earns interest at an annual rate of 8.4% compounded continuously. (A) Find the instantaneous rate of change of the amount in the account after 2 years. (B) Find the instantaneous rate of change of the amount in the account at t

> A mathematical model for the average of a group of people learning to type is given by N(t) = 10 + 6 ln t t ≥ 1 where N(t) is the number of words per minute typed after t hours of instruction and practice (2 hours per day, 5 days per week). What is t

> Blood pressure. Refer to Problem 71. Find the weight (to the nearest pound) at which the rate of change of blood pressure with respect to weight is 0.3 millimeter of mercury per pound. Data from Problem 71: An experiment was set up to find a relationshi

> Repeat Problem 69 for a starting colony of 1,000 bacteria such that a single bacterium divides every 0.25 hour. Data from Problem 69: A single cholera bacterium divides every 0.5 hour to produce two complete cholera bacteria. If we start with a colony o

> The estimated resale value R (in dollars) of a company car after t years is given by R(t) = 20,000(0.86)t What is the rate of depreciation (in dollars per year) after 1 year? 2 years? 3 years?

> Use the result of Problem 65 and the four-step process to show that if (x)= ecx, then (x)= cecx.

> use graphical approximation methods to find the points of intersection of ï¦(x) and g(x) (to two decimal places).

> use graphical approximation methods to find the points of intersection of ï¦(x) and g(x) (to two decimal places). [Note that there are two points of intersection and that ex is greater than x5 for large values of x.]

> Compute the odds against obtaining. 2 heads when a single coin is tossed twice.

> find dy/dx for the indicated function y. y = e3 - 3x

> find dy/dx for the indicated function y. y = -log2 x + 10 ln x

> find dy/dx for the indicated function y. y = x5 - 5x

> find dy/dx for the indicated function y. y = log x + 4x2 + 1

> find dy/dx for the indicated function y. y = 4x

Question: Find  (x) and find the equation of