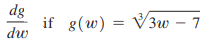[SOLVED] find the indicated derivative and simplify. /

> Use implicit differentiation to find yâ² and evaluate yâ² at the indicated point.

> What is the probability of getting at least 1 black card in a 7-card hand dealt from a standard 52-card deck?

> Use implicit differentiation to find yâ² and evaluate yâ² at the indicated point.

> Use implicit differentiation to find y′ and evaluate y′ at the indicated point. 5x3 - y - 1 = 0; (1, 4)

> Find y′ in two ways: (A) Differentiate the given equation implicitly and then solve for y′. (B) Solve the given equation for y and then differentiate directly. x + ln y = 1

> Find y′ in two ways: (A) Differentiate the given equation implicitly and then solve for y′. (B) Solve the given equation for y and then differentiate directly. 4x2 - ey = 10

> Find y′ in two ways: (A) Differentiate the given equation implicitly and then solve for y′. (B) Solve the given equation for y and then differentiate directly. x3 + y3 = 1

> Find y′ in two ways: (A) Differentiate the given equation implicitly and then solve for y′. (B) Solve the given equation for y and then differentiate directly. 2x + 9y = 12

> In Problems a sample space S is described. Would it be reasonable to make the equally likely assumption? Explain. A nickel and dime are tossed. We are interested in the number of heads that appear, so an appropriate sample space is S = 50, 1, 26.

> Replace ? with an expression that will make the indicated equation valid.

> Find ï¦â²(x)

> Find ′(x) (x) = 5 - 6x5

> A yeast culture at room temperature (68°F) is placed in a refrigerator set at a constant temperature of 38°F. After t hours, the temperature T of the culture is given approximately by T = 30e-0.58t + 38 t ≥ 0 What is the rate of change of temperature o

> The use of iodine crystals is a popular way of making small quantities of water safe to drink. Crystals placed in a 1-ounce bottle of water will dissolve until the solution is saturated. After saturation, half of the solution is poured into a quart conta

> The number x of bicycle helmets people are willing to buy per week from a retail chain at a price of $p is given by (A) Find dx / dp. (B) Find the demand and the instantaneous rate of change of demand with respect to price when the price is $75. Write

> A single card is drawn from a standard 52-card deck. Calculate the probability of each event. A heart or a number less than 7 (count an ace as 1) is drawn.

> The total cost (in hundreds of dollars) of producing x cameras per week is (A) Find Câ²(x). (B) Find Câ²(15) and Câ²(24). Interpret the results.

> Find each derivative and simplify.

> Give the domain of ï¦, the domain of g, and the domain of m, where m(x) = ï¦ [g(x)].

> In Problems a sample space S is described. Would it be reasonable to make the equally likely assumption? Explain. A single fair coin is tossed. We are interested in whether the coin falls heads or tails, so an appropriate sample space is S = 5H, T6.

> Give the domain of ï¦, the domain of g, and the domain of m, where m(x) = ï¦ [g(x)].

> A student reasons that the functions ï¦(x) = (x + 1)ln (x + 1) - x and g(x) = (x + 1)1/3 must have the same derivative since she has entered ï¦ (x), g(x), ï¦ â²(x), and gâ&#128

> Find ï¦â²(x) and find the value(s) of x where the tangent line is horizontal.

> Find ï¦â²(x) and find the equation of the line tangent to the graph of ï¦ï at the indicated value of x.

> find the indicated derivative and simplify.

> A single card is drawn from a standard 52-card deck. Calculate the probability of each event. A king or a heart is drawn.

> find the indicated derivative and simplify.

> Find the indicated derivative and simplify.

> Find ï¦â²(x)and the equation of the line tangent to the graph of ï¦ at the indicated value of x. Find the value(s) of x where the tangent line is horizontal.

> Find ï¦â²(x) and simplify.

> An experiment consists of tossing three fair (not weighted) coins, except that one of the three coins has a head on both sides. Compute the probability of obtaining the indicated results. More than 1tail

> Find ï¦â²(x) and simplify.

> Replace ? with an expression that will make the indicated equation valid.

> Find (A) the derivative of T(x) / B(x) without using the quotient rule, and (B) Tâ²(x) / Bâ²(x). Note that the answer to part (B) is different from the answer to part (A).

> Use these frequencies to calculate the approximate empirical probabilities and odds for the events (A) The sum is a prime number or is exactly divisible by 4. (B) The sum is an odd number or exactly divisible by 3

> Exercises write the expression as a quotient of integers, reduced to lowest terms.

> Find (A) the derivative of F(x) S(x) without using the product rule, and (B) Fâ²(x) Sâ²(x). Note that the answer to part (B) is different from the answer to part (A)

> One hour after a dose of x milligrams of a particular drug is administered to a person, the change in body temperature T(x), in degrees Fahrenheit, is given approximately by The rate Tâ²(x) at which T changes with respect to the size of

> According to economic theory, the supply x of a quantity in a free market increases as the price p increases (see the figure). Suppose that the number x of DVD players a retail chain is willing to sell per week at a price of $p is given by (A) Find dx

> A communications company has installed a new cable television system in a city. The total number N (in thousands) of subscribers t months after the installation of the system is given by (A) Find Nâ²(t). (B) Find N(16) and Nâ&#1

> Find each indicated derivative and simplify.

> An experiment consists of tossing three fair (not weighted) coins, except those one of the three coins has a head on both sides. Compute the probability of obtaining the indicated results. 0 Heads

> Find each indicated derivative and simplify.

> Find ï¦â²(x) in two ways: (1) using the product or quotient rule and (2) simplifying first.

> Find ï¦â² (x) and find the value(s) of x where ï¦â² (x) = 0.

> Find ï¦ (x) and find the equation of the line tangent to the graph of ï¦ at x = 2.

> (A) What are the odds for rolling a sum of 10 in a single roll of two fair dice? (B) If you bet $1 that a sum of 10 will turn up, what should the house pay (plus returning your $1 bet) if a sum of 10 turns up in order for the game to be fair? A pair of

> Find ï¦ (x) and find the equation of the line tangent to the graph of ï¦ at x = 2.

> (A) Find ï¦(x) using the quotient rule, and (B) Explain how ï¦(x) can be found easily without using the quotient rule.

> Find the indicated derivatives and simplify.

> find the indicated derivatives and simplify.

> Find the indicated derivatives and simplify.

> Find hâ²(x), where ï¦(x) is an unspecified differentiable function.

Question: find the indicated derivative and simplify. /