Question: The total cost (in hundreds of dollars)
The total cost (in hundreds of dollars) of producing x cameras per week is
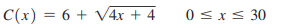
(A) Find C′(x).
(B) Find C′(15) and C′(24). Interpret the results.
> Assume that x = x(t) and y = y(t). Find the indicated rate, given the other information. x2 - 2xy - y2 = 7; dy/dt = -1 when x = 2 and y = -1; find dx/dt
> Assume that x = x(t) and y = y(t). Find the indicated rate, given the other information. x2 + y2 = 4; dy/dt = 5 when x = 1.2 and y = -1.6; find dx/dt
> if it is possible to solve for y in terms of x, do so. If not, write “Impossible.” y2 + ex y + x3 = 0
> if it is possible to solve for y in terms of x, do so. If not, write “Impossible.” 2 ln y + y ln x = 3x
> What is the probability that a number selected at random from the first 60 positive integers is (exactly) divisible by 6 or 9?
> if it is possible to solve for y in terms of x, do so. If not, write “Impossible.” 4y2 - x2 = 36
> if it is possible to solve for y in terms of x, do so. If not, write “Impossible.” -4x2 + 3y + 12 = 0
> Refer to Problem 62. Find dF/dr and discuss the connection between dF/dr and dr/dF. Data from Problem 62: The equation is Newton’s law of universal gravitation. G is a constant and F is the gravitational force between two objects havi
> The equation is Newton’s law of universal gravitation. G is a constant and F is the gravitational force between two objects having masses m1 and m2 that are a distance r from each other. Use implicit differentiation to find dr/dF . Ass
> In Problem 59, find dV/dL by implicit differentiation. Data from problem 59: In biophysics, the equation (L + m) (V + n) = k is called the fundamental equation of muscle contraction, where m, n, and k are constants and V is the velocity of the shorteni
> The number x of compact refrigerators that an appliance chain is willing to sell per week at a price of $p is given by Use implicit differentiation to find dp/dx.
> The number x of fitness watches that people are willing to buy per week from an online retailer at a price of $p is given by x = 5,000 - 0.1p2 Use implicit differentiation to find dp/dx.
> Refer to the equation in Problem 53. Find the equation(s) of the tangent line(s) at the point(s) on the graph where y = -1. Round all approximate values to two decimal places. Equation from Problem 53:
> Find y′ and the slope of the tangent line to the graph of each equation at the indicated point.
> Find y′ and the slope of the tangent line to the graph of each equation at the indicated point.
> In Problems a sample space S is described. Would it be reasonable to make the equally likely assumption? Explain. A wheel of fortune has seven sectors of equal area colored red, orange, yellow, red, orange, yellow, and red. We are interested in the color
> Find y′ and the slope of the tangent line to the graph of each equation at the indicated point.
> Find y′ and the slope of the tangent line to the graph of each equation at the indicated point.
> Explain the difficulty that arises in solving x3 + y + xey = 1 for y as an explicit function of x. Find the slope of the tangent line to the graph of the equation at the point (0, 1).
> find the equation(s) of the tangent line(s) to the graphs of the indicated equations at the point(s) with the given value of x.
> find the equation(s) of the tangent line(s) to the graphs of the indicated equations at the point(s) with the given value of x.
> Refer to the equation and graph shown in the figure. Find the slopes of the tangent lines at the points on the graph where x = 0.2. Check your answers by visually estimating the slopes on the graph in the figure.
> find x′ for x = x(t) defined implicitly by the given equation. Evaluate x′ at the indicated point. x3 - tx2 - 4 = 0; (-3, -2)
> Use implicit differentiation to find y′ and evaluate y′ at the indicated point.
> Use implicit differentiation to find y′ and evaluate y′ at the indicated point.
> Use implicit differentiation to find y′ and evaluate y′ at the indicated point.
> What is the probability of getting at least 1 black card in a 7-card hand dealt from a standard 52-card deck?
> Use implicit differentiation to find y′ and evaluate y′ at the indicated point.
> Use implicit differentiation to find y′ and evaluate y′ at the indicated point.
> Use implicit differentiation to find y′ and evaluate y′ at the indicated point.
> Use implicit differentiation to find y′ and evaluate y′ at the indicated point.
> Use implicit differentiation to find y′ and evaluate y′ at the indicated point.
> Use implicit differentiation to find y′ and evaluate y′ at the indicated point. 5x3 - y - 1 = 0; (1, 4)
> Find y′ in two ways: (A) Differentiate the given equation implicitly and then solve for y′. (B) Solve the given equation for y and then differentiate directly. x + ln y = 1
> Find y′ in two ways: (A) Differentiate the given equation implicitly and then solve for y′. (B) Solve the given equation for y and then differentiate directly. 4x2 - ey = 10
> Find y′ in two ways: (A) Differentiate the given equation implicitly and then solve for y′. (B) Solve the given equation for y and then differentiate directly. x3 + y3 = 1
> Find y′ in two ways: (A) Differentiate the given equation implicitly and then solve for y′. (B) Solve the given equation for y and then differentiate directly. 2x + 9y = 12
> In Problems a sample space S is described. Would it be reasonable to make the equally likely assumption? Explain. A nickel and dime are tossed. We are interested in the number of heads that appear, so an appropriate sample space is S = 50, 1, 26.
> Replace ? with an expression that will make the indicated equation valid.
> Replace ? with an expression that will make the indicated equation valid.
> Replace ? with an expression that will make the indicated equation valid.
> Find ′(x)
> Find ′(x)
> Find ′(x)
> Find ′(x) (x) = 5 - 6x5
> A yeast culture at room temperature (68°F) is placed in a refrigerator set at a constant temperature of 38°F. After t hours, the temperature T of the culture is given approximately by T = 30e-0.58t + 38 t ≥ 0 What is the rate of change of temperature o
> The use of iodine crystals is a popular way of making small quantities of water safe to drink. Crystals placed in a 1-ounce bottle of water will dissolve until the solution is saturated. After saturation, half of the solution is poured into a quart conta
> The number x of bicycle helmets people are willing to buy per week from a retail chain at a price of $p is given by (A) Find dx / dp. (B) Find the demand and the instantaneous rate of change of demand with respect to price when the price is $75. Write
> A single card is drawn from a standard 52-card deck. Calculate the probability of each event. A heart or a number less than 7 (count an ace as 1) is drawn.
> Find each derivative and simplify.
> Find each derivative and simplify.
> Find each derivative and simplify.
> Find each derivative and simplify.
> Find each derivative and simplify.
> Find each derivative and simplify.
> Give the domain of , the domain of g, and the domain of m, where m(x) =  [g(x)].
> Give the domain of , the domain of g, and the domain of m, where m(x) =  [g(x)].
> Give the domain of , the domain of g, and the domain of m, where m(x) =  [g(x)].
> In Problems a sample space S is described. Would it be reasonable to make the equally likely assumption? Explain. A single fair coin is tossed. We are interested in whether the coin falls heads or tails, so an appropriate sample space is S = 5H, T6.
> Give the domain of , the domain of g, and the domain of m, where m(x) =  [g(x)].
> A student reasons that the functions (x) = (x + 1)ln (x + 1) - x and g(x) = (x + 1)1/3 must have the same derivative since she has entered  (x), g(x),  ′(x), and gâ€
> Find ′(x) and find the value(s) of x where the tangent line is horizontal.
> Find ′(x) and find the value(s) of x where the tangent line is horizontal.
> Find ′(x) and find the value(s) of x where the tangent line is horizontal.
> Find ′(x) and find the equation of the line tangent to the graph of ï‚¦ï€ at the indicated value of x.
> Find ′(x) and find the equation of the line tangent to the graph of ï‚¦ï€ at the indicated value of x.
> Find ′(x) and find the equation of the line tangent to the graph of ï‚¦ï€ at the indicated value of x.
> find the indicated derivative and simplify.
> find the indicated derivative and simplify.
> A single card is drawn from a standard 52-card deck. Calculate the probability of each event. A king or a heart is drawn.
> find the indicated derivative and simplify.
> find the indicated derivative and simplify.
> find the indicated derivative and simplify.
> find the indicated derivative and simplify.
> find the indicated derivative and simplify.
> Find the indicated derivative and simplify.
> Find ′(x)and the equation of the line tangent to the graph of  at the indicated value of x. Find the value(s) of x where the tangent line is horizontal.
> Find ′(x)and the equation of the line tangent to the graph of  at the indicated value of x. Find the value(s) of x where the tangent line is horizontal.
> Find ′(x)and the equation of the line tangent to the graph of  at the indicated value of x. Find the value(s) of x where the tangent line is horizontal.
> Find ′(x) and simplify.
> An experiment consists of tossing three fair (not weighted) coins, except that one of the three coins has a head on both sides. Compute the probability of obtaining the indicated results. More than 1tail
> Find ′(x) and simplify.
> Find ′(x) and simplify.
> Find ′(x) and simplify.
> Find ′(x) and simplify.
> Find ′(x) and simplify.
> Find ′(x) and simplify.
> Find ′(x) and simplify.
> Find ′(x) and simplify.
> Replace ? with an expression that will make the indicated equation valid.
> Find (A) the derivative of T(x) / B(x) without using the quotient rule, and (B) T′(x) / B′(x). Note that the answer to part (B) is different from the answer to part (A).
> Use these frequencies to calculate the approximate empirical probabilities and odds for the events (A) The sum is a prime number or is exactly divisible by 4. (B) The sum is an odd number or exactly divisible by 3
> Exercises write the expression as a quotient of integers, reduced to lowest terms.
> Find (A) the derivative of F(x) S(x) without using the product rule, and (B) F′(x) S′(x). Note that the answer to part (B) is different from the answer to part (A)
> Find (A) the derivative of F(x) S(x) without using the product rule, and (B) F′(x) S′(x). Note that the answer to part (B) is different from the answer to part (A)
> One hour after a dose of x milligrams of a particular drug is administered to a person, the change in body temperature T(x), in degrees Fahrenheit, is given approximately by The rate T′(x) at which T changes with respect to the size of
> According to economic theory, the supply x of a quantity in a free market increases as the price p increases (see the figure). Suppose that the number x of DVD players a retail chain is willing to sell per week at a price of $p is given by (A) Find dx
> A communications company has installed a new cable television system in a city. The total number N (in thousands) of subscribers t months after the installation of the system is given by (A) Find N′(t). (B) Find N(16) and Nâ
> Find each indicated derivative and simplify.
> Find each indicated derivative and simplify.

