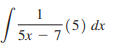[SOLVED] Find each indefinite integral and check the

> A manufacturing firm has budgeted $60,000 per month for labor and materials. If $x thousand is spent on labor and $y thousand is spent on materials, and if the monthly output (in units) is given by N(x, y) = 4xy - 8x then how should the $60,000 be alloc

> Consider the problem of minimizing. (A) Solve the constraint equation for y, and then substitute into ( (x, y) to obtain a function h(x) of the single variable x. Solve the original minimization problem by minimizing h (round answers to three decimal pl

> Consider the problem of minimizing ((x, y) subject to g(x, y) = 0, where g(x, y) = 4x - y + 3. Explain how the minimization problem can be solved without using the method of Lagrange multipliers.

> use Theorem 1 to explain why no maxima or minima exist.

> Use the method of Lagrange multipliers.

> Find each indefinite integral and check the result by differentiating.

> Use the method of Lagrange multipliers.

> Use the method of Lagrange multipliers. Minimize the product of two numbers if their difference must be 10.

> Use the method of Lagrange multipliers Find the maximum and minimum of ((x, y) = x2 - y2 subject to x2 + y2 = 25.

> use Theorem 1 to explain why no maxima or minima exist.

> Use the method of Lagrange multipliers.

> find (â²(0), ( â³(0), and determine whether f has a local minimum, local maximum, or neither at x = 0.

> Find each indefinite integral. Check by differentiating.

> find (â²(0), ( â³(0), and determine whether f has a local minimum, local maximum, or neither at x = 0.

> A shipping box is to be reinforced with steel bands in all three directions, as shown in the figure. A total of 150 inches of steel tape is to be used, with 6 inches of waste because of a 2-inch overlap in each direction. Find the dimensions of the box w

> A rectangular box with no top and two intersecting partitions (see the figure) must hold a volume of 72 cubic inches. Find the dimensions that will require the least material.

> Repeat Problem 45, replacing the coordinates of B with B(6, 9) and the coordinates of C with C(9, 0). Data from Problem 45: A satellite TV station is to be located at P1x, y2 so that the sum of the squares of the distances from P to the three towns A, B

> A store sells two brands of laptop sleeves. The store pays $25 for each brand A sleeve and $30 for each brand B sleeve. A consulting firm has estimated the daily demand equations for these two competitive products to be x = 130 - 4p + q Demand equation

> The annual labor and automated equipment cost (in millions of dollars) for a companyâs production of HDTVs is given by where x is the amount spent per year on labor and y is the amount spent per year on automated equipment (both in mi

> (A) Show that (0, 0) is a critical point of the function g(x, y) = exy2 + x2 y3 + 2, but that the second derivative test for local extrema fails. (B) Use cross sections, as in Example 2, to decide whether g has a local maximum, a local minimum, or a sad

> (A) Find the local extrema of the functions (B) Discuss the local extrema of the function K(x, y) = xn + yn , where n is a positive integer.

> Use Theorem 2 to find the local extrema.

> Find each indefinite integral and check the result by differentiating.

> Use Theorem 2 to find the local extrema.

> find (x(x, y)and (y(x, y), and explain, using Theorem 1, why ((x, y) has no local extrema.

> Find each indefinite integral. Check by differentiating.

> find (x(x, y)and (y(x, y), and explain, using Theorem 1, why ((x, y) has no local extrema.

> Find the indicated derivative.

> Poiseuilleâs law states that the resistance R for blood flowing in a blood vessel varies directly as the length L of the vessel and inversely as the fourth power of its radius r. Stated as an equation, Find RL(4, 0.2) and Rr(4, 0.2), a

> Use this test in Problem to determine whether the indicated products are competitive, complementary, or neither. The monthly demand equations for the sale of tennis rackets and tennis balls in a sporting goods store are

> Use this test in Problem to determine whether the indicated products are competitive, complementary, or neither. The daily demand equations for the saleÂ of brand A coffee and brand B coffee in a supermarketÂ are x = ((p, q) = 200

> The productivity of an automobile manufacturing company is given approximately by the function ((x, y = 50√xy = 50x0.5 y0.5 with the utilization of x units of labor and y units of capital. (A) Find (x(x, y) and (y(x, y). (B) If the company is now usin

> A company manufactures 10- and 3-speed bicycles. The weekly demand and cost functions are where $p is the price of a 10-speed bicycle, $q is the price of a 3-speed bicycle, x is the weekly demand for 10-speed bicycles, y is the weekly demand for 3-spee

> A company spends $x per week on online advertising and $y per week on TV advertising. Its weekly sales were found to be given by S(x, y) = 10x0.4y0.8 Find Sx(3,000, 2,000) and Sy(3,000, 2,000), and interpret the results.

> For ((x, y) = 2xy2 , find

> Let ((x, y) = ex + 2ey + 3xy2 + 1. (A) Use graphical approximation methods to find d (to three decimal places) such that ((1, d) is the minimum value of ((x, y) when x = 1. (B) Find (x(1, d) and (y(1, d).

> Let ((x, y) = 5 - 2x + 4y - 3x2 - y2 . (A) Find the maximum value of ( (x, y) when x = 2. (B) Explain why the answer to part (A) is not the maximum value of the function ( (x, y).

> For G(x, y) = x2 ln y - 3x - 2y + 1 find all values of x and y such that Gx(x, y) = 0 and Gy(x, y) = 0 simultaneously.

> For C(x, y) = 2x2 + 2xy + 3y2 - 16x - 18y + 54 find all values of x and y such that Cx(x, y) = 0 and Cy(x, y) = 0 simultaneously.

> Find (xx(x, y),(xy (x, y), (yx(x, y), and (yy(x, y) for each function (.

> Find each indefinite integral. Check by differentiating.

> Find (xx(x, y),(xy (x, y), (yx(x, y), and (yy(x, y) for each function (.

> (A) Find an example of a function ((x, y) such that ∂(/∂x = 3 and ∂(/∂y = 2. (B) How many such functions are there? Explain.

> S(T, r) = 50(T – 40)(5 – r) gives an ice cream shop’s daily sale as a function of temperature T (in °F) and rain r (in inches). Find the indicated quantity (include the appropriate units) and explain what it means. Srt(90, 1)

> S(T, r) = 50(T – 40)(5 – r) gives an ice cream shop’s daily sale as a function of temperature T (in °F) and rain r (in inches). Find the indicated quantity (include the appropriate units) and explain what it means. ST(90, 1)

> S(T, r) = 50(T – 40)(5 – r) gives an ice cream shop’s daily sale as a function of temperature T (in °F) and rain r (in inches). Find the indicated quantity (include the appropriate units) and explain what it means. S(80, 0)

> Find the indicated function or value if C(x, y) = 3x2 + 10xy - 8y2 + 4x - 15y - 120. Cyy(3, -2)

> Find the indicated function or value if C(x, y) = 3x2 + 10xy - 8y2 + 4x - 15y - 120. Cyx(x, y)

> Find the indicated function or value if C(x, y) = 3x2 + 10xy - 8y2 + 4x - 15y - 120. Cyy(x, y)

> Find the indicated function or value if C(x, y) = 3x2 + 10xy - 8y2 + 4x - 15y - 120. Cy(3, -2)

> Find the indicated function or value if C(x, y) = 3x2 + 10xy - 8y2 + 4x - 15y - 120.

> Find each indefinite integral and check the result by differentiating.

> could the given matrix be the transition matrix of an absorbing Markov chain?

> Find the indicated second-order partial derivative for each function ((x, y).

> M(x, y) = 68 + 0.3x - 0.8y gives the mileage (in mpg) of a new car as a function of tire pressure x (in psi) and speed (in mph). Find the indicated quantity (include the appropriate units) and explain what it means. My(32, 50)

> M(x, y) = 68 + 0.3x - 0.8y gives the mileage (in mpg) of a new car as a function of tire pressure x (in psi) and speed (in mph). Find the indicated quantity (include the appropriate units) and explain what it means. M(22, 50)

> M(x, y) = 68 + 0.3x - 0.8y gives the mileage (in mpg) of a new car as a function of tire pressure x (in psi) and speed (in mph). Find the indicated quantity (include the appropriate units) and explain what it means. M(22, 40)

> find the indicated value.

> Find each indefinite integral. Check by differentiating.

> find the indicated value.

> Find the indicated first-order partial derivative for each function z = ((x, y)

> Find the indicated derivative.

> Find each indefinite integral and check the result by differentiating.

> Find the indicated derivative.

> find the indicated value of the function of two or three variables. The height of a right circular cylinder is 6 feet and the diameter is also 6 feet. Find the total surface area.?

> find the indicated value of the function of two or three variables. The length, width, and height of a rectangular box are 30 centimeters, 15 centimeters, and 10 centimeters, respectively. Find the volume.

> find the indicated value of the function of two or three variables. The height of a trapezoid is 4 meters and the lengths of its parallel sides are 25 meters and 32 meters. Find the area.

> The force F of attraction between two masses m1 and m2 at distance r is given by Newtonâs law of universal gravitation where G is a constant. Evaluate F(50, 100, 20) and F(50, 100, 40).

> Under ideal conditions, if a person driving a car slam on the brakes and skids to a stop, the length of the skid marks (in feet) is given by the formula For k = 0.000 013 3, find L(2,000, 40) and L(3,000, 60).

Question: Find each indefinite integral and check the