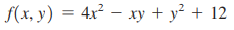[SOLVED] Use Theorem 2 to find the local

> (A) Give an example of a set of six data points such that half of the points lie above the least squares line and half lie below. (B) Give an example of a set of six data points such that just one of the points lies above the least squares line and five

> Refer to the system of normal equations and the formulas for a and b given on page 841. are the averages of the x and y coordinates, respectively, show that the point (x, y) satisfies the equation of the least squares line, y = ax + b.

> Repeat Problem 21 for the points (-1, -2), (0, 1), (1, 2), and (2, 0). Data from Problem 21:

> Find the least squares line and use it to estimate y for the indicated value of x. round answers to two decimal places.

> find the least squares line. Graph the data and the least squares line.

> Maximize or minimize subject to the constraint without using the method of Lagrange multipliers; instead, solve the constraint for x or y and substitute into ((x, y).

> Find each indefinite integral. Check by differentiating.

> Maximize or minimize subject to the constraint without using the method of Lagrange multipliers; instead, solve the constraint for x or y and substitute into ((x, y).

> A group of guinea pigs is to receive 25,600 calories per week. Two available foods produce 200xy calories for a mixture of x kilograms of type M food and y kilograms of type N food. If type M costs $1 per kilogram and type N costs $2 per kilogram, how mu

> A mailing service states that a rectangular package shall have the sum of its length and girth not to exceed 120 inches (see the figure on page 838). What are the dimensions of the largest (in volume) mailing carton that can be constructed to meet these

> The research department of a manufacturing company arrived at the following Cobb–Douglas production function for a particular product: N(x, y) = 10x0.6y0.4 In this equation, x is the number of units of labor and y is the number of units of capital requi

> A manufacturing firm has budgeted $60,000 per month for labor and materials. If $x thousand is spent on labor and $y thousand is spent on materials, and if the monthly output (in units) is given by N(x, y) = 4xy - 8x then how should the $60,000 be alloc

> Consider the problem of minimizing. (A) Solve the constraint equation for y, and then substitute into ( (x, y) to obtain a function h(x) of the single variable x. Solve the original minimization problem by minimizing h (round answers to three decimal pl

> Consider the problem of minimizing ((x, y) subject to g(x, y) = 0, where g(x, y) = 4x - y + 3. Explain how the minimization problem can be solved without using the method of Lagrange multipliers.

> use Theorem 1 to explain why no maxima or minima exist.

> Use the method of Lagrange multipliers.

> Find each indefinite integral and check the result by differentiating.

> Use the method of Lagrange multipliers.

> Use the method of Lagrange multipliers. Minimize the product of two numbers if their difference must be 10.

> Use the method of Lagrange multipliers Find the maximum and minimum of ((x, y) = x2 - y2 subject to x2 + y2 = 25.

> use Theorem 1 to explain why no maxima or minima exist.

> Use the method of Lagrange multipliers.

> find (â²(0), ( â³(0), and determine whether f has a local minimum, local maximum, or neither at x = 0.

> Find each indefinite integral. Check by differentiating.

> find (â²(0), ( â³(0), and determine whether f has a local minimum, local maximum, or neither at x = 0.

> A shipping box is to be reinforced with steel bands in all three directions, as shown in the figure. A total of 150 inches of steel tape is to be used, with 6 inches of waste because of a 2-inch overlap in each direction. Find the dimensions of the box w

> A rectangular box with no top and two intersecting partitions (see the figure) must hold a volume of 72 cubic inches. Find the dimensions that will require the least material.

> Repeat Problem 45, replacing the coordinates of B with B(6, 9) and the coordinates of C with C(9, 0). Data from Problem 45: A satellite TV station is to be located at P1x, y2 so that the sum of the squares of the distances from P to the three towns A, B

> A store sells two brands of laptop sleeves. The store pays $25 for each brand A sleeve and $30 for each brand B sleeve. A consulting firm has estimated the daily demand equations for these two competitive products to be x = 130 - 4p + q Demand equation

> The annual labor and automated equipment cost (in millions of dollars) for a companyâs production of HDTVs is given by where x is the amount spent per year on labor and y is the amount spent per year on automated equipment (both in mi

> (A) Show that (0, 0) is a critical point of the function g(x, y) = exy2 + x2 y3 + 2, but that the second derivative test for local extrema fails. (B) Use cross sections, as in Example 2, to decide whether g has a local maximum, a local minimum, or a sad

> (A) Find the local extrema of the functions (B) Discuss the local extrema of the function K(x, y) = xn + yn , where n is a positive integer.

> Use Theorem 2 to find the local extrema.

> Find each indefinite integral and check the result by differentiating.

> Use Theorem 2 to find the local extrema.

> find (x(x, y)and (y(x, y), and explain, using Theorem 1, why ((x, y) has no local extrema.

> Find each indefinite integral. Check by differentiating.

> find (x(x, y)and (y(x, y), and explain, using Theorem 1, why ((x, y) has no local extrema.

> Find the indicated derivative.

> Poiseuilleâs law states that the resistance R for blood flowing in a blood vessel varies directly as the length L of the vessel and inversely as the fourth power of its radius r. Stated as an equation, Find RL(4, 0.2) and Rr(4, 0.2), a

> Use this test in Problem to determine whether the indicated products are competitive, complementary, or neither. The monthly demand equations for the sale of tennis rackets and tennis balls in a sporting goods store are

> Use this test in Problem to determine whether the indicated products are competitive, complementary, or neither. The daily demand equations for the saleÂ of brand A coffee and brand B coffee in a supermarketÂ are x = ((p, q) = 200

> Find each indefinite integral and check the result by differentiating.

> The productivity of an automobile manufacturing company is given approximately by the function ((x, y = 50√xy = 50x0.5 y0.5 with the utilization of x units of labor and y units of capital. (A) Find (x(x, y) and (y(x, y). (B) If the company is now usin

> A company manufactures 10- and 3-speed bicycles. The weekly demand and cost functions are where $p is the price of a 10-speed bicycle, $q is the price of a 3-speed bicycle, x is the weekly demand for 10-speed bicycles, y is the weekly demand for 3-spee

> A company spends $x per week on online advertising and $y per week on TV advertising. Its weekly sales were found to be given by S(x, y) = 10x0.4y0.8 Find Sx(3,000, 2,000) and Sy(3,000, 2,000), and interpret the results.

> For ((x, y) = 2xy2 , find

> Let ((x, y) = ex + 2ey + 3xy2 + 1. (A) Use graphical approximation methods to find d (to three decimal places) such that ((1, d) is the minimum value of ((x, y) when x = 1. (B) Find (x(1, d) and (y(1, d).

> Let ((x, y) = 5 - 2x + 4y - 3x2 - y2 . (A) Find the maximum value of ( (x, y) when x = 2. (B) Explain why the answer to part (A) is not the maximum value of the function ( (x, y).

> For G(x, y) = x2 ln y - 3x - 2y + 1 find all values of x and y such that Gx(x, y) = 0 and Gy(x, y) = 0 simultaneously.

> For C(x, y) = 2x2 + 2xy + 3y2 - 16x - 18y + 54 find all values of x and y such that Cx(x, y) = 0 and Cy(x, y) = 0 simultaneously.

> Find (xx(x, y),(xy (x, y), (yx(x, y), and (yy(x, y) for each function (.

> Find each indefinite integral. Check by differentiating.

> Find (xx(x, y),(xy (x, y), (yx(x, y), and (yy(x, y) for each function (.

> (A) Find an example of a function ((x, y) such that ∂(/∂x = 3 and ∂(/∂y = 2. (B) How many such functions are there? Explain.

> S(T, r) = 50(T – 40)(5 – r) gives an ice cream shop’s daily sale as a function of temperature T (in °F) and rain r (in inches). Find the indicated quantity (include the appropriate units) and explain what it means. Srt(90, 1)

> S(T, r) = 50(T – 40)(5 – r) gives an ice cream shop’s daily sale as a function of temperature T (in °F) and rain r (in inches). Find the indicated quantity (include the appropriate units) and explain what it means. ST(90, 1)

> S(T, r) = 50(T – 40)(5 – r) gives an ice cream shop’s daily sale as a function of temperature T (in °F) and rain r (in inches). Find the indicated quantity (include the appropriate units) and explain what it means. S(80, 0)

> Find the indicated function or value if C(x, y) = 3x2 + 10xy - 8y2 + 4x - 15y - 120. Cyy(3, -2)

> Find the indicated function or value if C(x, y) = 3x2 + 10xy - 8y2 + 4x - 15y - 120. Cyx(x, y)

> Find the indicated function or value if C(x, y) = 3x2 + 10xy - 8y2 + 4x - 15y - 120. Cyy(x, y)

> Find the indicated function or value if C(x, y) = 3x2 + 10xy - 8y2 + 4x - 15y - 120. Cy(3, -2)

> Find the indicated function or value if C(x, y) = 3x2 + 10xy - 8y2 + 4x - 15y - 120.

> Find each indefinite integral and check the result by differentiating.

> could the given matrix be the transition matrix of an absorbing Markov chain?

> Find the indicated second-order partial derivative for each function ((x, y).

> M(x, y) = 68 + 0.3x - 0.8y gives the mileage (in mpg) of a new car as a function of tire pressure x (in psi) and speed (in mph). Find the indicated quantity (include the appropriate units) and explain what it means. My(32, 50)

> M(x, y) = 68 + 0.3x - 0.8y gives the mileage (in mpg) of a new car as a function of tire pressure x (in psi) and speed (in mph). Find the indicated quantity (include the appropriate units) and explain what it means. M(22, 50)

> M(x, y) = 68 + 0.3x - 0.8y gives the mileage (in mpg) of a new car as a function of tire pressure x (in psi) and speed (in mph). Find the indicated quantity (include the appropriate units) and explain what it means. M(22, 40)

> find the indicated value.

> Find each indefinite integral. Check by differentiating.

> find the indicated value.

Question: Use Theorem 2 to find the local