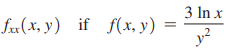[SOLVED] Find the indicated second-order partial derivative

> Use Theorem 2 to find the local extrema.

> Find each indefinite integral and check the result by differentiating.

> Use Theorem 2 to find the local extrema.

> find (x(x, y)and (y(x, y), and explain, using Theorem 1, why ((x, y) has no local extrema.

> Find each indefinite integral. Check by differentiating.

> find (x(x, y)and (y(x, y), and explain, using Theorem 1, why ((x, y) has no local extrema.

> Find the indicated derivative.

> Poiseuilleâs law states that the resistance R for blood flowing in a blood vessel varies directly as the length L of the vessel and inversely as the fourth power of its radius r. Stated as an equation, Find RL(4, 0.2) and Rr(4, 0.2), a

> Use this test in Problem to determine whether the indicated products are competitive, complementary, or neither. The monthly demand equations for the sale of tennis rackets and tennis balls in a sporting goods store are

> Use this test in Problem to determine whether the indicated products are competitive, complementary, or neither. The daily demand equations for the saleÂ of brand A coffee and brand B coffee in a supermarketÂ are x = ((p, q) = 200

> Find each indefinite integral and check the result by differentiating.

> The productivity of an automobile manufacturing company is given approximately by the function ((x, y = 50√xy = 50x0.5 y0.5 with the utilization of x units of labor and y units of capital. (A) Find (x(x, y) and (y(x, y). (B) If the company is now usin

> A company manufactures 10- and 3-speed bicycles. The weekly demand and cost functions are where $p is the price of a 10-speed bicycle, $q is the price of a 3-speed bicycle, x is the weekly demand for 10-speed bicycles, y is the weekly demand for 3-spee

> A company spends $x per week on online advertising and $y per week on TV advertising. Its weekly sales were found to be given by S(x, y) = 10x0.4y0.8 Find Sx(3,000, 2,000) and Sy(3,000, 2,000), and interpret the results.

> For ((x, y) = 2xy2 , find

> Let ((x, y) = ex + 2ey + 3xy2 + 1. (A) Use graphical approximation methods to find d (to three decimal places) such that ((1, d) is the minimum value of ((x, y) when x = 1. (B) Find (x(1, d) and (y(1, d).

> Let ((x, y) = 5 - 2x + 4y - 3x2 - y2 . (A) Find the maximum value of ( (x, y) when x = 2. (B) Explain why the answer to part (A) is not the maximum value of the function ( (x, y).

> For G(x, y) = x2 ln y - 3x - 2y + 1 find all values of x and y such that Gx(x, y) = 0 and Gy(x, y) = 0 simultaneously.

> For C(x, y) = 2x2 + 2xy + 3y2 - 16x - 18y + 54 find all values of x and y such that Cx(x, y) = 0 and Cy(x, y) = 0 simultaneously.

> Find (xx(x, y),(xy (x, y), (yx(x, y), and (yy(x, y) for each function (.

> Find each indefinite integral. Check by differentiating.

> Find (xx(x, y),(xy (x, y), (yx(x, y), and (yy(x, y) for each function (.

> (A) Find an example of a function ((x, y) such that ∂(/∂x = 3 and ∂(/∂y = 2. (B) How many such functions are there? Explain.

> S(T, r) = 50(T – 40)(5 – r) gives an ice cream shop’s daily sale as a function of temperature T (in °F) and rain r (in inches). Find the indicated quantity (include the appropriate units) and explain what it means. Srt(90, 1)

> S(T, r) = 50(T – 40)(5 – r) gives an ice cream shop’s daily sale as a function of temperature T (in °F) and rain r (in inches). Find the indicated quantity (include the appropriate units) and explain what it means. ST(90, 1)

> S(T, r) = 50(T – 40)(5 – r) gives an ice cream shop’s daily sale as a function of temperature T (in °F) and rain r (in inches). Find the indicated quantity (include the appropriate units) and explain what it means. S(80, 0)

> Find the indicated function or value if C(x, y) = 3x2 + 10xy - 8y2 + 4x - 15y - 120. Cyy(3, -2)

> Find the indicated function or value if C(x, y) = 3x2 + 10xy - 8y2 + 4x - 15y - 120. Cyx(x, y)

> Find the indicated function or value if C(x, y) = 3x2 + 10xy - 8y2 + 4x - 15y - 120. Cyy(x, y)

> Find the indicated function or value if C(x, y) = 3x2 + 10xy - 8y2 + 4x - 15y - 120. Cy(3, -2)

> Find the indicated function or value if C(x, y) = 3x2 + 10xy - 8y2 + 4x - 15y - 120.

> Find each indefinite integral and check the result by differentiating.

> could the given matrix be the transition matrix of an absorbing Markov chain?

> Find the indicated second-order partial derivative for each function ((x, y).

> M(x, y) = 68 + 0.3x - 0.8y gives the mileage (in mpg) of a new car as a function of tire pressure x (in psi) and speed (in mph). Find the indicated quantity (include the appropriate units) and explain what it means. My(32, 50)

> M(x, y) = 68 + 0.3x - 0.8y gives the mileage (in mpg) of a new car as a function of tire pressure x (in psi) and speed (in mph). Find the indicated quantity (include the appropriate units) and explain what it means. M(22, 50)

> M(x, y) = 68 + 0.3x - 0.8y gives the mileage (in mpg) of a new car as a function of tire pressure x (in psi) and speed (in mph). Find the indicated quantity (include the appropriate units) and explain what it means. M(22, 40)

> find the indicated value.

> Find each indefinite integral. Check by differentiating.

> find the indicated value.

> Find the indicated first-order partial derivative for each function z = ((x, y)

> Find the indicated derivative.

> Find each indefinite integral and check the result by differentiating.

> Find the indicated derivative.

> find the indicated value of the function of two or three variables. The height of a right circular cylinder is 6 feet and the diameter is also 6 feet. Find the total surface area.?

> find the indicated value of the function of two or three variables. The length, width, and height of a rectangular box are 30 centimeters, 15 centimeters, and 10 centimeters, respectively. Find the volume.

> find the indicated value of the function of two or three variables. The height of a trapezoid is 4 meters and the lengths of its parallel sides are 25 meters and 32 meters. Find the area.

> The force F of attraction between two masses m1 and m2 at distance r is given by Newtonâs law of universal gravitation where G is a constant. Evaluate F(50, 100, 20) and F(50, 100, 40).

> Under ideal conditions, if a person driving a car slam on the brakes and skids to a stop, the length of the skid marks (in feet) is given by the formula For k = 0.000 013 3, find L(2,000, 40) and L(3,000, 60).

> Poiseuilleâs law states that the resistance R for blood flowing in a blood vessel varies directly as the length L of the vessel and inversely as the fourth power of its radius r. Stated as an equation, Find R(8, 1) and R(4, 0.2).

> The packaging department in a company has been asked to design a rectangular box with no top and a partition down the middle (see the figure). Let x, y, and z be the dimensions of the box (in inches). Ignore the thickness of the material from which the b

> The petroleum company in Problem 69 is taken over by another company that decides to double both the units of labor and the units of capital utilized in the production of petroleum. Use the Cobb–Douglas production function given in Problem 69 to find the

> A company manufactures 10- and 3-speed bicycles. The weekly demand and cost equations are p = 230 - 9x + y q = 130 + x - 4y C(x, y) = 200 + 80x + 30y where $p is the price of a 10-speed bicycle, $q is the price of a 3-speed bicycle, x is the weekly dema

> Find each indefinite integral. Check by differentiating.

> A company spends $x thousand per week on online advertising and $y thousand per week on TV advertising. Its weekly sales are found to be given by S(x, y) = 5x2 y3 Find S(3, 2) and S(2, 3)

> Let f1x, y2 = 4 - √x2 + y2 . (A) Explain why f1a, b2 = f1c, d2 whenever 1a, b2 and 1c, d2 are points on the same circle with center at the origin in the xy plane. (B) Describe the cross sections of the surface z = ((x, y) produced by cutting it with th

> Let ((x, y) = 100 + 10x + 25y - x2 - 5y2 . (A) Describe the cross sections of the surface z = ((x, y) produced by cutting it with the planes y = 0, y = 1, y = 2, and y = 3. (B) Describe the cross sections of the surface in the planes x = 0, x = 1, x =

> Let ((x, y) = √4 - y2 . (A) Explain why the cross sections of the surface z = ((x, y) produced by cutting it with planes parallel to x = 0 are semicircles of radius 2. (B) Describe the cross sections of the surface in the planes y = 0, y = 2, and y = 3

> Find the coordinates of B and H in the figure for Matched Problem 6 on page 807.

> For the function ((x, y) = 2xy2 , find

> For the function ((x, y) = x2 + 2y2 , find

> Let G(a, b, c) = a3 + b3 + c3 – (ab + ac + bc) - 6. Find all values of b such that G(2, b, 1) = 0.

> Let F(x, y) = xy + 2x2 + y2 - 25. Find all values of y such that F(y, y) = 0.

> Let F(x, y) = 5x - 4y + 12. Find all values of x such that F(x, 0) = 0.

> Find each indefinite integral and check the result by differentiating.

> Find a formula for the function K(C, h) of two variables that gives the volume of a right circular cone of circumference C and height h.

> Find a formula for the function T(x, y, z) of three variables that gives the square of the distance from the point (x, y, z) to the origin (0, 0, 0).

> Find a formula for the function W(x1, x2, x3, x4) of four variables that gives the total volume of oil that can be carried in four oil tankers of capacities x1, x2, x3, and x4, respectively.

> Find a formula for the function N( p, r) of two variables that gives the number of hot dogs sold at a baseball game, if p is the price per hot dog and r is the total amount received from the sale of hot dogs.

> Find a formula for the function V(d, h) of two variables that gives the volume of a right circular cylinder of diameter d and height h.

> find the indicated function f of a single variable.

> find the indicated value of the given function.

Question: Find the indicated second-order partial derivative