Question: Find the x-values (if any) at
Find the x-values (if any) at which f is not continuous. Which of the discontinuities are removable?
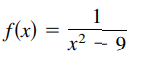
> Find the vertical asymptotes (if any) of the graph of the function. f(x) = csc πx
> Find the vertical asymptotes (if any) of the graph of the function.
> Find the vertical asymptotes (if any) of the graph of the function.
> Find the vertical asymptotes (if any) of the graph of the function.
> Find the vertical asymptotes (if any) of the graph of the function.
> Find the vertical asymptotes (if any) of the graph of the function.
> Find the vertical asymptotes (if any) of the graph of the function.
> Find the vertical asymptotes (if any) of the graph of the function.
> Find the vertical asymptotes (if any) of the graph of the function.
> Find the vertical asymptotes (if any) of the graph of the function.
> In your own words, describe what is meant by a vertical asymptote of a graph.
> Find the vertical asymptotes (if any) of the graph of the function.
> Find the vertical asymptotes (if any) of the graph of the function.
> A utility company burns coal to generate electricity. The cost C in dollars of removing p% of the air pollutants in the stack emissions is Find the cost of removing 50% of the pollutants. Find the cost of removing 90% of the pollutants. Find the limit
> Find the one-sided limit (if it exists).
> Find the one-sided limit (if it exists).
> Find the one-sided limit (if it exists).
> Find the one-sided limit (if it exists).
> Find the one-sided limit (if it exists).
> Find the one-sided limit (if it exists).
> Find the one-sided limit (if it exists).
> Find the one-sided limit (if it exists).
> Find the one-sided limit (if it exists).
> Find the vertical asymptotes (if any) of the graph of the function.
> Find the one-sided limit (if it exists).
> Find the vertical asymptotes (if any) of the graph of the function.
> Find the vertical asymptotes (if any) of the graph of the function.
> Find the vertical asymptotes (if any) of the graph of the function.
> Find the vertical asymptotes (if any) of the graph of the function.
> Find the vertical asymptotes (if any) of the graph of the function.
> Find the vertical asymptotes (if any) of the graph of the function.
> Determine whether f (x) approaches ∞ or −∞ as x approaches 6 from the left and from the right.
> Determine whether f (x) approaches ∞ or −∞ as x approaches 6 from the left and from the right.
> Verify that the Intermediate Value Theorem applies to the indicated interval and find the value of c guaranteed by the theorem. has at least two zeros in the interval [−3, 3].
> Create a table of values for the function and use the result to determine whether f (x) approaches ∞ or −∞ as x approaches −3 from the left and from the right. Use a graphing utility to graph the function to confirm your answer. f(x) = tan (πx / 6)
> Verify that the Intermediate Value Theorem applies to the indicated interval and find the value of c guaranteed by the theorem. has at least two zeros in the interval [−3, 3].
> Use the Intermediate Value Theorem to show that has at least two zeros in the interval [−3, 3].
> Use the Intermediate Value Theorem to show that has a zero in the interval [1, 2].
> Describe the intervals on which the function is continuous.
> Describe the intervals on which the function is continuous.
> Describe the intervals on which the function is continuous.
> Describe the intervals on which the function is continuous.
> Describe the intervals on which the function is continuous.
> Describe the intervals on which the function is continuous.
> Find the values of b and c such that the function is continuous on the entire real number line.
> Create a table of values for the function and use the result to determine whether f (x) approaches ∞ or −∞ as x approaches −3 from the left and from the right. Use a graphing utility to graph the function to confirm your answer. f(x) = cot (πx / 3)
> Find the value of c such that the function is continuous on the entire real number line.
> Find the x-values (if any) at which f is not continuous. Which of the discontinuities are removable?
> Find the x-values (if any) at which f is not continuous. Which of the discontinuities are removable?
> Find the x-values (if any) at which f is not continuous. Which of the discontinuities are removable?
> Find the x-values (if any) at which f is not continuous. Which of the discontinuities are removable?
> Find the x-values (if any) at which f is not continuous. Which of the discontinuities are removable?
> Discuss the continuity of the function on the closed interval.
> Discuss the continuity of the function on the closed interval.
> Find the limit (if it exists). If it does not exist, explain why.
> Create a table of values for the function and use the result to determine whether f (x) approaches ∞ or −∞ as x approaches −3 from the left and from the right. Use a graphing utility to graph the function to confirm your answer. f(x) = -1 / 3 + x
> Find the limit (if it exists). If it does not exist, explain why.
> Find the limit (if it exists). If it does not exist, explain why.
> Find the limit (if it exists). If it does not exist, explain why.
> Find the limit (if it exists). If it does not exist, explain why.
> Find the limit (if it exists). If it does not exist, explain why.
> Find the limit (if it exists). If it does not exist, explain why.
> Find the limit (if it exists). If it does not exist, explain why.
> Find the limit (if it exists). If it does not exist, explain why.
> Find the limit (if it exists). If it does not exist, explain why.
> Find the limit (if it exists). If it does not exist, explain why.
> Create a table of values for the function and use the result to determine whether f (x) approaches ∞ or −∞ as x approaches −3 from the left and from the right. Use a graphing utility to graph the function to confirm your answer. f(x) = x2 / (x2 – 9)
> Find the limit (if it exists). If it does not exist, explain why.
> Use the position function s(t) = -4.9t2 + 250, which gives the height (in meters) of an object that has fallen for t seconds from a height of 250 meters. The velocity at time t = a seconds is given by When will the object hit the ground? At what ve
> Use the position function s(t) = -4.9t2 + 250, which gives the height (in meters) of an object that has fallen for t seconds from a height of 250 meters. The velocity at time t = a seconds is given by Find the velocity of the object when t = 4
> Use a graphing utility to graph the function and estimate the limit. Use a table to reinforce your conclusion. Then find the limit by analytic methods.
> Use a graphing utility to graph the function and estimate the limit. Use a table to reinforce your conclusion. Then find the limit by analytic methods.
> Use a graphing utility to graph the function and estimate the limit. Use a table to reinforce your conclusion. Then find the limit by analytic methods.
> Use a graphing utility to graph the function and estimate the limit. Use a table to reinforce your conclusion. Then find the limit by analytic methods.
> Evaluate the limit given f(x) = -6 and g(x) = ½.
> Evaluate the limit given f(x) = -6 and g(x) = 1/2
> Evaluate the limit given f(x) = -6 and g(x) = ½.
> Create a table of values for the function and use the result to determine whether f (x) approaches ∞ or −∞ as x approaches −3 from the left and from the right. Use a graphing utility to graph the function to confirm your answer. f(x) = x / (x2 – 9)
> Evaluate the limit given f(x) = -6 and g(x) = ½.
> Find the limit. [Hint: cos(θ + ϕ) = cos θ cos ϕ − sin θ sin ϕ]
> Find the limit. [Hint: sin(θ + ϕ) = sin θ cos ϕ + cos θ sin ϕ]
> Find the limit.
> Find the limit.
> Find the limit.
> Find the limit.
> Find the limit.
> Find the limit.
> Find the limit.
> Create a table of values for the function and use the result to determine whether f (x) approaches ∞ or −∞ as x approaches −3 from the left and from the right. Use a graphing utility to graph the function to confirm your answer. f(x) = 1 / (x2 – 9)
> Find the limit.
> Find the limit.
> Find the limit.
> Find the limit.
> Find the limit.
> Find the limit.
> Find the limit.
> Find the limit.
> Find the limit.
> Find the limit L. Then use the ε-δ definition to prove that the limit is L.
> Determine whether f(x) approaches ∞ or −∞ as x approaches 4 from the left and from the right. f(x) = -1 / (x – 4)2

