Question: Use a graphing utility to graph the
Use a graphing utility to graph the function and estimate the limit. Use a table to reinforce your conclusion. Then find the limit by analytic methods.
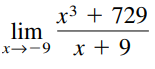
> Find the vertical asymptotes (if any) of the graph of the function.
> Find the one-sided limit (if it exists).
> Find the vertical asymptotes (if any) of the graph of the function.
> Find the vertical asymptotes (if any) of the graph of the function.
> Find the vertical asymptotes (if any) of the graph of the function.
> Find the vertical asymptotes (if any) of the graph of the function.
> Find the vertical asymptotes (if any) of the graph of the function.
> Find the vertical asymptotes (if any) of the graph of the function.
> Determine whether f (x) approaches ∞ or −∞ as x approaches 6 from the left and from the right.
> Determine whether f (x) approaches ∞ or −∞ as x approaches 6 from the left and from the right.
> Verify that the Intermediate Value Theorem applies to the indicated interval and find the value of c guaranteed by the theorem. has at least two zeros in the interval [−3, 3].
> Create a table of values for the function and use the result to determine whether f (x) approaches ∞ or −∞ as x approaches −3 from the left and from the right. Use a graphing utility to graph the function to confirm your answer. f(x) = tan (πx / 6)
> Verify that the Intermediate Value Theorem applies to the indicated interval and find the value of c guaranteed by the theorem. has at least two zeros in the interval [−3, 3].
> Use the Intermediate Value Theorem to show that has at least two zeros in the interval [−3, 3].
> Use the Intermediate Value Theorem to show that has a zero in the interval [1, 2].
> Describe the intervals on which the function is continuous.
> Describe the intervals on which the function is continuous.
> Describe the intervals on which the function is continuous.
> Describe the intervals on which the function is continuous.
> Describe the intervals on which the function is continuous.
> Describe the intervals on which the function is continuous.
> Find the values of b and c such that the function is continuous on the entire real number line.
> Create a table of values for the function and use the result to determine whether f (x) approaches ∞ or −∞ as x approaches −3 from the left and from the right. Use a graphing utility to graph the function to confirm your answer. f(x) = cot (πx / 3)
> Find the value of c such that the function is continuous on the entire real number line.
> Find the x-values (if any) at which f is not continuous. Which of the discontinuities are removable?
> Find the x-values (if any) at which f is not continuous. Which of the discontinuities are removable?
> Find the x-values (if any) at which f is not continuous. Which of the discontinuities are removable?
> Find the x-values (if any) at which f is not continuous. Which of the discontinuities are removable?
> Find the x-values (if any) at which f is not continuous. Which of the discontinuities are removable?
> Find the x-values (if any) at which f is not continuous. Which of the discontinuities are removable?
> Discuss the continuity of the function on the closed interval.
> Discuss the continuity of the function on the closed interval.
> Find the limit (if it exists). If it does not exist, explain why.
> Create a table of values for the function and use the result to determine whether f (x) approaches ∞ or −∞ as x approaches −3 from the left and from the right. Use a graphing utility to graph the function to confirm your answer. f(x) = -1 / 3 + x
> Find the limit (if it exists). If it does not exist, explain why.
> Find the limit (if it exists). If it does not exist, explain why.
> Find the limit (if it exists). If it does not exist, explain why.
> Find the limit (if it exists). If it does not exist, explain why.
> Find the limit (if it exists). If it does not exist, explain why.
> Find the limit (if it exists). If it does not exist, explain why.
> Find the limit (if it exists). If it does not exist, explain why.
> Find the limit (if it exists). If it does not exist, explain why.
> Find the limit (if it exists). If it does not exist, explain why.
> Find the limit (if it exists). If it does not exist, explain why.
> Create a table of values for the function and use the result to determine whether f (x) approaches ∞ or −∞ as x approaches −3 from the left and from the right. Use a graphing utility to graph the function to confirm your answer. f(x) = x2 / (x2 – 9)
> Find the limit (if it exists). If it does not exist, explain why.
> Use the position function s(t) = -4.9t2 + 250, which gives the height (in meters) of an object that has fallen for t seconds from a height of 250 meters. The velocity at time t = a seconds is given by When will the object hit the ground? At what ve
> Use the position function s(t) = -4.9t2 + 250, which gives the height (in meters) of an object that has fallen for t seconds from a height of 250 meters. The velocity at time t = a seconds is given by Find the velocity of the object when t = 4
> Use a graphing utility to graph the function and estimate the limit. Use a table to reinforce your conclusion. Then find the limit by analytic methods.
> Use a graphing utility to graph the function and estimate the limit. Use a table to reinforce your conclusion. Then find the limit by analytic methods.
> Use a graphing utility to graph the function and estimate the limit. Use a table to reinforce your conclusion. Then find the limit by analytic methods.
> Evaluate the limit given f(x) = -6 and g(x) = ½.
> Evaluate the limit given f(x) = -6 and g(x) = 1/2
> Evaluate the limit given f(x) = -6 and g(x) = ½.
> Create a table of values for the function and use the result to determine whether f (x) approaches ∞ or −∞ as x approaches −3 from the left and from the right. Use a graphing utility to graph the function to confirm your answer. f(x) = x / (x2 – 9)
> Evaluate the limit given f(x) = -6 and g(x) = ½.
> Find the limit. [Hint: cos(θ + ϕ) = cos θ cos ϕ − sin θ sin ϕ]
> Find the limit. [Hint: sin(θ + ϕ) = sin θ cos ϕ + cos θ sin ϕ]
> Find the limit.
> Find the limit.
> Find the limit.
> Find the limit.
> Find the limit.
> Find the limit.
> Find the limit.
> Create a table of values for the function and use the result to determine whether f (x) approaches ∞ or −∞ as x approaches −3 from the left and from the right. Use a graphing utility to graph the function to confirm your answer. f(x) = 1 / (x2 – 9)
> Find the limit.
> Find the limit.
> Find the limit.
> Find the limit.
> Find the limit.
> Find the limit.
> Find the limit.
> Find the limit.
> Find the limit.
> Find the limit L. Then use the ε-δ definition to prove that the limit is L.
> Determine whether f(x) approaches ∞ or −∞ as x approaches 4 from the left and from the right. f(x) = -1 / (x – 4)2
> In your own words, describe the meaning of an infinite limit. What does ∞ represent?
> At age 14 months, Reggie built a block tower and gleefully knocked it down. At age 2, he called to his mother and pointed proudly to his tall block tower. What explains this change in Reggie’s emotional behaviour?
> Several times, after her father hid a teething biscuit under a red cup, 12-month-old Mimi retrieved it easily. Then Mimi’s father hid the biscuit under a nearby yellow cup. Why did Mimi persist in searching for it under the red cup?
> Which infant enrichment program would you choose: one that emphasizes gentle talking and touching and social games, or one that includes reading and number drills and classical music lessons? Explain.
> On seeing her new-born baby for the first time, Caroline exclaimed, “Why is she so out of proportion?” What observations prompted Caroline to ask this question? Explain why her baby’s appearance is adaptive.
> Rhonda and Mark, a career-oriented couple in their early thirties, are thinking about having a baby. What factors should they keep in mind as they decide whether to add to their family at this time in their lives?
> Gilbert’s genetic makeup is homozygous for dark hair. Jan’s is homozygous for blond hair. What proportion of their children are likely to be dark-haired? Explain.
> Why is it ethically important for researchers to offer the intervention to the no-intervention control group after completion of the study?
> Explain how factors that promote resilience contribute to children’s favourable adjustment following divorce.
> What style do gifted children who realize their potential typically experience? Explain.
> Is the concept of authoritative child rearing useful for understanding effective parenting across cultures? Explain.
> Imagine that you must counsel a couple considering in vitro fertilization using donor ova to overcome infertility. What medical and ethical risks would you raise?
> Explain how children’s strategies for word learning support the interactionist perspective on language development.
> According to differentiation theory, perceptual development reflects infants’ active search for invariant features. Provide examples from research on hearing, pattern perception, object perception, and intermodal perception.
> Explain how generous employment leave for childbirth—at least 12 weeks of paid time off available to either the mother or father—can ease the transition to parenthood and promote positive parent–infant interaction.
> Derek, father of a 3-year-old and a new-born, reported that he had a harder time adjusting to the birth of his second child than to that of his first. Explain why this might be so.
> Claire told her 6-year-old daughter never to talk to or take candy from strangers. Why is Claire’s warning unlikely to protect her daughter from sexual abuse? What preventive actions can Claire take?
> Sandy wonders why her daughter Mira’s teacher often has students work on assignments in small, cooperative groups. Explain the benefits of this approach to Sandy. What must Mira’s teacher do to ensure that cooperative learning succeeds?
> Chandra heard a news report about 10 severely neglected children, living in squalor in an inner-city tenement. She wondered, “Why would parents so mistreat their children?” How would you answer Chandra?
> Sammy’s mother explained to him that the family would take a vacation in Miami. The next morning, Sammy announced, “I gotted my bags packed. When are we going to Your-ami?” What explains Sammy’s errors?
> Ben, age 13 months, has just started to walk. Using the concept of affordances, explain why he is likely to step over risky drop-offs.
> What strengths and limitations do the clinical, or case study, method and ethnography have in common?
> Provide an example of how one domain of development (physical, cognitive, or emotional/social) can affect development in another domain.

