[SOLVED] If an object moves along the y

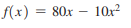
> One hour after x milligrams of a particular drug are given to a person, the change in body temperature T (in degrees Fahrenheit) is given by Approximate the changes in body temperature produced by the following changes in drug dosages: (A) From 2 to 2.

> An egg of a particular bird is nearly spherical. If the radius to the inside of the shell is 5 millimeters and the radius to the outside of the shell is 5.3 millimeters, approximately what is the volume of the shell? Remember that:

> A company manufactures and sells x televisions per month. If the cost and revenue equations are what will the approximate changes in revenue and profit be if production is increased from 1,500 to 1,510? From 4,500 to 4,510?

> Suppose that the daily demand (in pounds) for chocolate candy at $x per pound is given by D = 1,000 - 40x2 1 ≤ x ≤ 5 If the price is increased from $3.00 per pound to $3.20 per pound, what is the approximate change in demand?

> Find dy and ∆y for y = 590 / √x, x = 64, and ∆x = dx = 1.

> Find dy if y = (2x2 – 4) √x.

> discuss the validity of each statement. If the statement is always true, explain why. If not, give a counterexample. Suppose that y = (x) defines a function whose domain is the set of all real numbers. If every increment at x = 2 is equal to 0, then (x

> discuss the validity of each statement. If the statement is always true, explain why. If not, give a counterexample. If the graph of the function y = (x) is a parabola, then the functions ∆y and dy (of the independent variable ∆x = dx) for (x) at x = 0

> An experiment consists of rolling two fair dice and adding the dots on the two sides facing up. Using the sample space shown in Figure 2 (page 398) and, assuming each simple event is as likely as any other, find the probability of the sum of the dots ind

> (A) Find ây and dy for the function f at the indicated value of x. (B) Graph ây and dy from part (A) as functions of âx. (C) Compare the values of ây and dy from part (A) at the in

> A sphere with a radius of 5 centimeters is coated with ice 0.1 centimeter thick. Use differentials to estimate the volume of the ice.

> evaluate dy and ây for each function for the indicated values.

> find dy for each function.

> find dy for each function. y = (2x + 3)2

> find the indicated quantities for y = ï¦(x) = 3x2 .

> find dy for each function.

> Discuss the validity of each statement. If the statement is always true, explain why. If not, give a counterexample. If the odds for E are a: b, then the odds against E are b: a.

> find dy for each function.

> find the indicated quantities for y = ï¦ (x) = 5x2 .

> let g(x) = x2 and find the given values without using a calculator

> write the expression in the form xn .

> If a person learns y items in x hours, as given by find the rate of learning at the end of (A) 1 hour (B) 8 hours

> An experiment consists of rolling two fair dice and adding the dots on the two sides facing up. Using the sample space shown in Figure 2 (page 398) and, assuming each simple event is as likely as any other, find the probability of the sum of the dots ind

> A coal-burning electrical generating plant emits sulfur dioxide into the surrounding air. The concentration C(x), in parts per million, is given approximately by where x is the distance from the plant in miles. Find the instantaneous rate of change of c

> The percentages of female high school graduates who enrolled in college are given in the third column of Table 1. (A) Let x represent time (in years) since 1970, and let y represent the corresponding percentage of female high school graduates who enroll

> Suppose that, in a given gourmet food store, people are willing to buy x pounds of chocolate candy per day at $p per quarter pound, as given by the priceâ demand equation This function is graphed in the figure. Find the demand and the

> A company’s total sales (in millions of dollars) t months from now are given by S(t) = 0.015t4 + 0.4t3 + 3.4t2 + 10t - 3 (A) Find S′(t). (B) Find S(4) and S′(4) (to two decimal places). Write a brief verbal interpretation of these results. (C) Find S(8

> Let (x) = u(x) - v(x), where u′(x) and v′(x) exist. Use the four-step process to show that  = (x) = u′(x) - v′(x).

> Discuss the validity of each statement. If the statement is always true, explain why. If not, give a counterexample. The derivative of a constant times a function is 0.

> Discuss the validity of each statement. If the statement is always true, explain why. If not, give a counterexample. The derivative of a quotient is the quotient of the derivatives.

> Find the indicated derivatives.

> Find the indicated derivatives. y′ if y = (2x – 5)2

> Compute the probability of event E if the odds in favor of E are. Answer:

> Can a cubic polynomial function have more than two horizontal tangents? Explain.

> Now that you know how to find derivatives, explain why it is no longer necessary for you to memorize the formula for the x coordinate of the vertex of a parabola.

> Require the use of a graphing calculator. For each problem, find ï¦â(x) and approximate (to four decimal places) the value(s) of x where the graph of f has a horizontal tangent line.

> If an object moves along the y axis (marked in feet) so that its position at time x (in seconds) is given by the indicated functions. Find (A) The instantaneous velocity function v =ï¦ â(x) (B) The velocity when x = 0

> Find (A) ï¦ï (x) (B) The slope of the graph of ï¦ at x = 2 and x = 4 (C) The equations of the tangent lines at x = 2 and x = 4 (D) The value(s) of x where the tangent line is horizontal

> Suppose that 6 people check their coats in a checkroom. If all claim checks are lost and the 6 coats are randomly returned, what is the probability that all the people will get their own coats back?

> Find the indicated derivatives.

> Given the following probabilities for an event E, find the odds for and against E:

> Write the expression as a quotient of integers, reduced to lowest terms.

> Find the indicated derivatives.

> Refer to functions f and g that satisfy ï¦â (2) = 3 and gâ (2) = -1. In each problem, find hâ (2) for the indicated function h.

> Find the indicated derivatives.

> In a three-way race for the U.S. Senate, polls indicate that the two leading candidates are running neck-and-neck, while the third candidate is receiving half the support of either of the others. Registered voters are chosen at random and asked which of

> Find the indicated derivatives.

> Find the indicated derivatives. g′(x) for g(x) = x9

> Find the indicated derivatives. y′ for y = x8

> Find the indicated derivatives.

> Write the expression in the form a + b1n where a and b are reduced fractions and n is an integer

> Find the slope of the line through the given points. Write the slope as a reduced fraction, and also give its decimal form. Answer:

> Find the slope of the line through the given points. Write the slope as a reduced fraction, and also give its decimal form.

> The body temperature (in degrees Fahrenheit) of a patient t hours after taking a fever-reducing drug is given by (A) Use the four-step process to find F= (t). (B) Find F(3) and F= (3). Write a brief verbal interpretation of these results.

> Refer to the data in Table 1. (A) Let x represent time (in years) with x = 0 corresponding to 2000, and let y represent the corresponding commercial sales. Enter the appropriate data set in a graphing calculator and find a quadratic regression equation

> Use the equally likely sample space in Example 2 to compute the probability of the following events: The number on the first die is even or the number on the second die is even.

> The U.S. consumption of refined copper (in thousands of metric tons) is given approximately by P(t) = 48t2 - 37t + 1,698 where t is time in years and t = 0 corresponds to 2010. (A) Use the four-step process to find p′(t). (B) Find the annual consumptio

> A company’s total sales (in millions of dollars) t months from now are given by S(t) = √t + 8 (A) Use the four-step process to find S′1t2. (B) Find S(9) and S′(9). Write a brief verbal interpretation of these results. (C) Use the results in part (B)

> The profit (in dollars) from the sale of x infant car seats is given by P(x) = 45x - 0.025x2 - 5,000 0 ≤ x ≤ 2,400 (A) Find the average change in profit if production is changed from 800 car seats to 850 car seats. (B) Use the four-step process to fin

> Repeat Problem 79 if the balloon is 1,024 feet above the ground when the ball is dropped. Data from Problem 79: A ball dropped from a balloon falls y = 16x2 feet in x seconds. If the balloon is 576 feet above the ground when the ball is dropped, when do

> Determine whether ï¦ is differentiable at x = 0 by considering

> Determine whether ï¦ is differentiable at x = 0 by considering ï¦(x) = x2/3

> Determine whether ï¦ is differentiable at x = 0 by considering ï¦(x) = 1 - | x |

> sketch the graph of ï¦ and determine where ï¦ is nondifferentiable.

> Discuss the validity of each statement. If the statement is always true, explain why. If not, give a counterexample. If the graph of f has a sharp corner at x = a, then f is not continuous at x = a

> Refer to the description of a standard deck of 52 cards and Figure 4 on page 384. An experiment consists of dealing 5 cards from a standard 52-card deck. In Problems what is the probability of being dealt. Figure 4: 5 nonface cards.

> Discuss the validity of each statement. If the statement is always true, explain why. If not, give a counterexample. if a function f is differentiable on the interval (a, b), then f is continuous on (a, b)

> Discuss the validity of each statement. If the statement is always true, explain why. If not, give a counterexample. If (x) = mx + b is a linear function, then ’(x) = m.

> Let (x) = -x2 , g(x) = -x2 - 1, and h(x) = -x2 + 2. (A) How are the graphs of these functions related? How would you expect the derivatives of these functions to be related? (B) Use the four-step process to find the derivative of m(x) = -x2 + C, whe

Question: If an object moves along the y