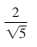[SOLVED] Write the expression in the form a +

> The percentages of female high school graduates who enrolled in college are given in the third column of Table 1. (A) Let x represent time (in years) since 1970, and let y represent the corresponding percentage of female high school graduates who enroll

> Suppose that, in a given gourmet food store, people are willing to buy x pounds of chocolate candy per day at $p per quarter pound, as given by the priceâ demand equation This function is graphed in the figure. Find the demand and the

> A company’s total sales (in millions of dollars) t months from now are given by S(t) = 0.015t4 + 0.4t3 + 3.4t2 + 10t - 3 (A) Find S′(t). (B) Find S(4) and S′(4) (to two decimal places). Write a brief verbal interpretation of these results. (C) Find S(8

> Let (x) = u(x) - v(x), where u′(x) and v′(x) exist. Use the four-step process to show that  = (x) = u′(x) - v′(x).

> Discuss the validity of each statement. If the statement is always true, explain why. If not, give a counterexample. The derivative of a constant times a function is 0.

> Discuss the validity of each statement. If the statement is always true, explain why. If not, give a counterexample. The derivative of a quotient is the quotient of the derivatives.

> Find the indicated derivatives.

> Find the indicated derivatives. y′ if y = (2x – 5)2

> Compute the probability of event E if the odds in favor of E are. Answer:

> Can a cubic polynomial function have more than two horizontal tangents? Explain.

> Now that you know how to find derivatives, explain why it is no longer necessary for you to memorize the formula for the x coordinate of the vertex of a parabola.

> Require the use of a graphing calculator. For each problem, find ï¦â(x) and approximate (to four decimal places) the value(s) of x where the graph of f has a horizontal tangent line.

> If an object moves along the y axis (marked in feet) so that its position at time x (in seconds) is given by the indicated functions. Find (A) The instantaneous velocity function v =ï¦ â(x) (B) The velocity when x = 0

> Find (A) ï¦ï (x) (B) The slope of the graph of ï¦ at x = 2 and x = 4 (C) The equations of the tangent lines at x = 2 and x = 4 (D) The value(s) of x where the tangent line is horizontal

> Suppose that 6 people check their coats in a checkroom. If all claim checks are lost and the 6 coats are randomly returned, what is the probability that all the people will get their own coats back?

> Find the indicated derivatives.

> Given the following probabilities for an event E, find the odds for and against E:

> Write the expression as a quotient of integers, reduced to lowest terms.

> Find the indicated derivatives.

> Refer to functions f and g that satisfy ï¦â (2) = 3 and gâ (2) = -1. In each problem, find hâ (2) for the indicated function h.

> Find the indicated derivatives.

> In a three-way race for the U.S. Senate, polls indicate that the two leading candidates are running neck-and-neck, while the third candidate is receiving half the support of either of the others. Registered voters are chosen at random and asked which of

> Find the indicated derivatives.

> Find the indicated derivatives. g′(x) for g(x) = x9

> Find the indicated derivatives. y′ for y = x8

> Find the indicated derivatives.

> Write the expression in the form a + b1n where a and b are reduced fractions and n is an integer

> Find the slope of the line through the given points. Write the slope as a reduced fraction, and also give its decimal form. Answer:

> Find the slope of the line through the given points. Write the slope as a reduced fraction, and also give its decimal form.

> The body temperature (in degrees Fahrenheit) of a patient t hours after taking a fever-reducing drug is given by (A) Use the four-step process to find F= (t). (B) Find F(3) and F= (3). Write a brief verbal interpretation of these results.

> Refer to the data in Table 1. (A) Let x represent time (in years) with x = 0 corresponding to 2000, and let y represent the corresponding commercial sales. Enter the appropriate data set in a graphing calculator and find a quadratic regression equation

> Use the equally likely sample space in Example 2 to compute the probability of the following events: The number on the first die is even or the number on the second die is even.

> The U.S. consumption of refined copper (in thousands of metric tons) is given approximately by P(t) = 48t2 - 37t + 1,698 where t is time in years and t = 0 corresponds to 2010. (A) Use the four-step process to find p′(t). (B) Find the annual consumptio

> A company’s total sales (in millions of dollars) t months from now are given by S(t) = √t + 8 (A) Use the four-step process to find S′1t2. (B) Find S(9) and S′(9). Write a brief verbal interpretation of these results. (C) Use the results in part (B)

> The profit (in dollars) from the sale of x infant car seats is given by P(x) = 45x - 0.025x2 - 5,000 0 ≤ x ≤ 2,400 (A) Find the average change in profit if production is changed from 800 car seats to 850 car seats. (B) Use the four-step process to fin

> Repeat Problem 79 if the balloon is 1,024 feet above the ground when the ball is dropped. Data from Problem 79: A ball dropped from a balloon falls y = 16x2 feet in x seconds. If the balloon is 576 feet above the ground when the ball is dropped, when do

> Determine whether ï¦ is differentiable at x = 0 by considering

> Determine whether ï¦ is differentiable at x = 0 by considering ï¦(x) = x2/3

> Determine whether ï¦ is differentiable at x = 0 by considering ï¦(x) = 1 - | x |

> sketch the graph of ï¦ and determine where ï¦ is nondifferentiable.

> Discuss the validity of each statement. If the statement is always true, explain why. If not, give a counterexample. If the graph of f has a sharp corner at x = a, then f is not continuous at x = a

> Refer to the description of a standard deck of 52 cards and Figure 4 on page 384. An experiment consists of dealing 5 cards from a standard 52-card deck. In Problems what is the probability of being dealt. Figure 4: 5 nonface cards.

> Discuss the validity of each statement. If the statement is always true, explain why. If not, give a counterexample. if a function f is differentiable on the interval (a, b), then f is continuous on (a, b)

> Discuss the validity of each statement. If the statement is always true, explain why. If not, give a counterexample. If (x) = mx + b is a linear function, then ’(x) = m.

> Let (x) = -x2 , g(x) = -x2 - 1, and h(x) = -x2 + 2. (A) How are the graphs of these functions related? How would you expect the derivatives of these functions to be related? (B) Use the four-step process to find the derivative of m(x) = -x2 + C, whe

> Repeat Problem 59 with (x) = 8x2 - 4x. Data from Problem 59: If an object moves along a line so that it is at y = (x) = 4x2 - 2x at time x (in seconds), find the instantaneous velocity function v = (x) and find the velocity at times x = 1, 3, and 5

> (A) Find  = (x). (B) Find the slopes of the lines tangent to the graph of  at x = 0, 2, and 4. (C) Graph  and sketch in the tangent lines at x = 0, 2, and 4.  (x) = 4x - x2 + 1

> Refer to the function F in the graph shown. Use the graph to determine whether Fâ(x) exists at each indicated value of x x = h

> Refer to the function F in the graph shown. Use the graph to determine whether Fâ(x) exists at each indicated value of x x = ï¦.

> Refer to the function F in the graph shown. Use the graph to determine whether Fâ(x) exists at each indicated value of x x = d

> Refer to the function F in the graph shown. Use the graph to determine whether Fâ(x) exists at each indicated value of x x = b

> suppose an object moves along the y axis so that its location is y = (x) = x2 + x at time x (y is in meters and x is in seconds). Find (A) The average velocity (the average rate of change of y with respect to x) for x changing from 2 to 4 seconds (B) T

> Use the equally likely sample space in Example 2 to compute the probability of the following events: A sum that is greater than 9.

> Refer to the graph of y = ( (x) = x2 + x shown. (A) Find the slope of the secant line joining (2, ï¦(2)) and (4, ï¦(4)). (B) Find the slope of the secant line joining (2, ï¦(2)) and (2 + h, ï&#

> Use the four-step process to find ( = (x) and then find ( = (1) , ( = (2), and ( = (3).

> Refer to the description of a standard deck of 52 cards and Figure 4 on page 384. An experiment consists of dealing 5 cards from a standard 52-card deck. what is the probability of being dealt. Figure 4: 5 Hearts?/

> Use the four-step process to find ( = (x) and then find ( = (1) , ( = (2), and ( = (3).

> For ((x) = x4 , the instantaneous rate of change is known to be -4 at x = -1. Find the equation of the tangent line to the graph of y = ((x) at the point with x coordinate -1.

> For( (x) = 1 / + x2, the slope of the graph of y = ( (x) is known to be -0.16 at the point with x coordinate 2. Find the equation of the tangent line at that point.

> Four hours after the start of a 600-mile auto race, a driverâs velocity is 150 miles per hour as she completes the 352nd lap on a 1.5-mile track.

> Find the indicated quantities for f(x) = 3x2 .

>

> Use interval notation to specify the given interval.

> If the probability is .03 that an automobile tire fails in less than 50,000 miles, what is the probability that the tire does not fail in 50,000 miles?

> Use interval notation to specify the given interval.

Question: Write the expression in the form a +