Question: Use a power series to approximate the
Use a power series to approximate the definite integral to six decimal places.
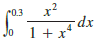
Transcribed Image Text:
.2 r0.3 dx 1 + x 4 Jo
> If p > 1, evaluate the expression
> Let Show that u3 + v3 + w3 - 3uvw = 1. .3 u = 1 + 3! 6! 9! 10 v = x + 4! 7! 10! w = 2! 5! 8! + + + +
> Suppose you have a large supply of books, all the same size, and you stack them at the edge of a table, with each book extending farther beyond the edge of the table than the one beneath it. Show that it is possible to do this so that the top book extend
> Find the sum of the series ∑∞n=1 ln (1 – 1/n2).
> Find the sum of the series where the terms are the reciprocals of the positive integers whose only prime factors are 2s and 3s. 1+ 3 4 6 8 12 +
> To construct the snowflake curve, start with an equilateral triangle with sides of length 1. Step 1 in the construction is to divide each side into three equal parts, construct an equilateral triangle on the middle part, and then delete the middle part (
> Find the area of the shaded region. r=
> Let {pn} be a sequence of points determined as in the figure. Thus |AP1| = 1, |PnPn+1| = 2n-1, and angle APnPn+1 is a right angle. Find limn→∞∠Pn APn+1. P4 4 P3 P2 ´A 1 P. P3
> If f (x) = sin (x3), find f(15)(0).
> 1. If limn→∞an = 0, then ∑an is convergent. 2. The series ∑∞n=1 n-sin 1 is convergent. 3.If limn→∞an = L, then limnâ†
> Find the Maclaurin series for f (x) using the definition of a Maclaurin series. [Assume that f has a power series expansion. Do not show that Rn (x) → 0.] Also find the associated radius of convergence. f(x) = cos 3x
> Find the Maclaurin series for f (x) using the definition of a Maclaurin series. [Assume that f has a power series expansion. Do not show that Rn (x) → 0.] Also find the associated radius of convergence. f(x): = sin 7x
> Find the Maclaurin series for f (x) using the definition of a Maclaurin series. [Assume that f has a power series expansion. Do not show that Rn (x) → 0.] Also find the associated radius of convergence. f() %—D In(1 + х) %3D
> Find the Maclaurin series for f (x) using the definition of a Maclaurin series. [Assume that f has a power series expansion. Do not show that Rn (x) → 0.] Also find the associated radius of convergence. f(x) = (1 – x)-2 %3D
> Find the Taylor series for f centered at 4 if What is the radius of convergence of the Taylor series? (-1)* п! fl(4) = 3(n + 1)
> Use a Maclaurin series in Table 1 to obtain the Maclaurin series for the given function. f(x) = sin'x [Hint: Use sin'x = }(1 – s 2x).] cos %3D
> Use a Maclaurin series in Table 1 to obtain the Maclaurin series for the given function. f(x) = x² In(1 + x³)
> Find the area of the region that is bounded by the given curve and lies in the specified sector. r= /sin 6, 0< 0 <T
> If f(n)(0) = (n + 1)! For n = 0, 1, 2, … find the Maclaurin series for f and its radius of convergence.
> Use a Maclaurin series in Table 1 to obtain the Maclaurin series for the given function. f(x) = x cos(}x²)
> Use a Maclaurin series in Table 1 to obtain the Maclaurin series for the given function. f(x) = cos(Tx/2)
> Use the binomial series to expand the function as a power series. State the radius of convergence. 1 (2 + x) 13
> Prove that the series obtained in Exercise 16 represents sin x for all x. Exercise 16: Find the Taylor series for f (x) centered at the given value of f. [Assume that has a power series expansion. Do not show that Rn (x) →0.] f(x
> Suppose you know that the series ∑∞n=0bnxn converges for |x| 00 ba Σ R-0 n + 1 n+1
> Prove that the series obtained in Exercise 7 represents sin Ï€x for all x. Exercise 7: Find the Maclaurin series for f (x) using the definition of a Maclaurin series. [Assume that f has a power series expansion. Do not show that Rn (x) â
> Find the Taylor series for f (x) centered at the given value of f. [Assume that has a power series expansion. Do not show that Rn (x) →0.] f(x) = x-2, a= 1
> Find the Taylor series for f (x) centered at the given value of f. [Assume that has a power series expansion. Do not show that Rn (x) →0.] f(x) = 1//x, a = 9
> Find the Taylor series for f (x) centered at the given value of f. [Assume that has a power series expansion. Do not show that Rn (x) →0.] f(x) = sin x, a = "/2
> Find the area of the region that is bounded by the given curve and lies in the specified sector. r = sin 0, 7/3 < 0 < 2m/3
> Find the Taylor series for f (x) centered at the given value of f. [Assume that has a power series expansion. Do not show that Rn (x) →0.] f(x) 3 сos x, а a = T
> Find the Taylor series for f (x) centered at the given value of f. [Assume that has a power series expansion. Do not show that Rn (x) →0.] f(x) = 1/x, a = -3
> Find the Taylor series for f (x) centered at the given value of f. [Assume that has a power series expansion. Do not show that Rn (x) →0.]
> Find the Taylor series for f (x) centered at the given value of f. [Assume that has a power series expansion. Do not show that Rn (x) →0.] f(x) = x – x', a= -2
> Find the Taylor series for f (x) centered at the given value of f. [Assume that has a power series expansion. Do not show that Rn (x) →0.] f(x) = x* – 3x? + 1, a = 1
> If f (x) = ∑∞n=0 bn (x – 5)n for all x, write a formula for bs.
> Find a power series representation for the function and determine the interval of convergence. 1 + x f(x) 1- x
> Find a power series representation for the function and determine the interval of convergence. f(x) = 2x? + 1
> Find a power series representation for the function and determine the interval of convergence. f(x) = 9 + x?
> Find a power series representation for the function and determine the interval of convergence. f(x) = x + 10
> Find the area of the region that is bounded by the given curve and lies in the specified sector. r= e /2
> Find a power series representation for the function and determine the interval of convergence.
> (a). By completing the square, show that (b). By factoring x3 + 1 as a sum of cubes, rewrite the integral in part (a). Then express 1/ (x3 + 1) as the sum of a power series and use it to prove the following formula for π: dx C1/2 Jo x -
> Find a power series representation for the function and determine the interval of convergence. 3 f(x) 1- x*
> Use the power series for tan-1x to prove the following expression for Ï€ as the sum of an infinite series: ㅠ=D 2v3 Σ (-1)" (2n + 1)3" R-0
> (a). Starting with the geometric series∑∞n=0xn, find the sum of the series (b). Find the sum of each of the following series. (c). Find the sum of each of the following series. 2 nx"-I -1 |x| (i) E nx", |x|<1
> The Bessel function of order 1 is defined by (a). Show that j1 satisfies the differential equation (b). Show that j10 (x) = -j1(x). Ji(x) = E (-1)^x²«+1 n!(n + 1)!22n+1 A-0 x³J*(x) + xJ{(x) + (x² – 1)J1(x) = 0
> (a). Show that j0 (the Bessel function of order 0 given in Example 4) satisfies the differential equation (b). Evaluate f10 j0 (x) dx correct to three decimal places. X²J®(x) + xJ¿(x) + x²J(x) = 0
> Show that the function is a solution of the differential equation f"(x) + f (x) = 0 (-1)"x2" f(x) = E %3! A-0 (2n)!
> Use the result of Example 7 to compute arctan 0.2 correct to five decimal places.
> Find the area of the region that is bounded by the given curve and lies in the specified sector. r= 0°, 0< 0 < /4
> Use a power series to approximate the definite integral to six decimal places. r0.1 "x arctan(3x) dx
> Use a power series to approximate the definite integral to six decimal places. r0.4 In(1 + x*) dx C04
> Use a power series to approximate the definite integral to six decimal places. 1 dx Jo 1+ x* r0.2
> Evaluate the indefinite integral as a power series. What is the radius of convergence? tan-(x²) dx
> Evaluate the indefinite integral as a power series. What is the radius of convergence? X - tan х — -dx .3
> Evaluate the indefinite integral as a power series. What is the radius of convergence? In(1 – t) dt t
> Evaluate the indefinite integral as a power series. What is the radius of convergence? t dt 1- 18
> Find a power series representation for f, and graph f and several partial sums sn (x) on the same screen. What happens as n increases? f(x) = tan-(2x)
> Find a power series representation for f, and graph f and several partial sums sn (x) on the same screen. What happens as n increases? 1+ x f(x) = In{ 1- x
> Find a power series representation for f, and graph f and several partial sums sn (x) on the same screen. What happens as n increases? f(x) = In(x² + 4)
> The astronomer Giovanni Cassini (1625–1712) studied the family of curves with polar equations where and are positive real numbers. These curves are called the ovals of Cassini even though they are oval shaped only for certain values o
> Find a power series representation for f, and graph f and several partial sums sn (x) on the same screen. What happens as n increases? f(x) : x? + 16
> Find a power series representation for the function and determine the radius of convergence. x? + x f(x) (1 – x)³
> Find a power series representation for the function and determine the radius of convergence. 1 + x f(x) = (1 – x)?
> Find a power series representation for the function and determine the radius of convergence. 13 f(x) = 2 - x
> Find a power series representation for the function and determine the radius of convergence. f(x) = (1 + 4x)?
> Find a power series representation for the function and determine the radius of convergence. f(x) = x²tan='(x³)
> Find a power series representation for the function and determine the radius of convergence. f(x) 3 In(5 — х)
> In Exercise 31 in Section 6.4 it was shown that the length of the ellipse x = a sin θ, y = b cos θ, where a > b > 0, is where e = √a2 – b2/a is the eccentricity of the ellipse. Expand
> Use the following steps to prove (17). (a). Let g (x) = ∑∞n=0 (k/n) xn. Differentiate this series to show that (b). Let h (x) = (1 + x)-k g (x) and show that h'(x) = 0. (c). Deduce that g (x) = (1 + x)k. kg(x) 1
> (a). Use Equation 1 to find a power series representation for f (x) = ln (1 – x). What is the radius of convergence? (b). Use part (a) to find a power series for f (x) = x ln (1 – x). (c). By putting x = 1/2 in your result from part (a), express ln 2 as
> A family of curves has polar equations Investigate how the graph changes as the number changes. In particular, you should identify the transitional values of a for which the basic shape of the curve changes. 1 — а сos a cos e 1 + a cos e
> Prove Taylor’s Inequality for n = 2, that is, prove that if |f"'(x)| M | R:(x) | <x - a for |x – a|<d 6.
> Find the sum of the series. 1/ 1∙2 – 1/3∙23 + 1/5∙ 25 – 1/7∙ 27 +…
> Find the sum of the series. 3 + 9/2! + 27/3! + 81/4! +…
> Find the sum of the series. 1 – ln2 + (ln2)2/2! - (ln2)2/2! +…
> Find the sum of the series. ∑∞n=0 (-1)n π2n+1/42n+1 (2n + 1)!
> Find the sum of the series. ∑∞n=0 3n/5nn!
> Find the sum of the series. ∑∞n=0 (-1)n-1 3n/n5n
> Find the sum of the series. ∑∞n=0 (-1)n π2n/62n (2n)!
> Find the sum of the series. ∑∞n=0 (-1)n x4n/n!
> Use multiplication or division of power series to find the first three nonzero terms in the Maclaurin series for each function. y = e* In(1 + x)
> A family of curves is given by the equations r = 1 + c sin nθ, where c is a real number and n is a positive integer. How does the graph change as increases? How does it change as c changes? Illustrate by graphing enough members of the family to support y
> Use multiplication or division of power series to find the first three nonzero terms in the Maclaurin series for each function. y sin x
> Use multiplication or division of power series to find the first three nonzero terms in the Maclaurin series for each function. y = sec x
> Use multiplication or division of power series to find the first three nonzero terms in the Maclaurin series for each function. y= e cos x
> Use the series in Example 13(b) to evaluate We found this limit in Example 4 in Section 4.5 using l’Hospital’s Rule three times. Which method do you prefer? tan x - x lim .3
> Use series to evaluate the limit. limx→0 sin x – x + 1/6 x3/ x5
> Use series to evaluate the limit. limx→0 1 – cos x/1 + x - ex
> Use series to evaluate the limit. limx→0 x – 1 ln (1 + x)/x2
> Use series to approximate the definite integral to within the indicated accuracy. x²e* dx ([error|< 0.001) Jo
> Use series to approximate the definite integral to within the indicated accuracy. L" VI + x* dx (lerror| < 5 x 10-9) *0.4
> Use series to approximate the definite integral to within the indicated accuracy. *0.2 " (tan-(x) + sin(x³)] dx (five decimal places)
> (a). Investigate the family of curves defined by the polar equations r = sin nθ, where n is a positive integer. How is the number of loops related to n? (b). What happens if the equation in part (a) is replaced by r = |sin nθ|?
> Use the given graph of f (x) = x2 to find a number δ such that if |x - 1|< 8 |x² – 1|<} then y y=x² 1.5 1+ 0.5 ? 1 ?
> Use series to approximate the definite integral to within the indicated accuracy. x cos(x') dx (three decimal places)
> Evaluate the indefinite integral as an infinite series. f arctan (x2), dx
> Evaluate the indefinite integral as an infinite series. f cos x – 1/x, dx
> (a). Show that the function defined by is not equal to its Maclaurin series. (b). Graph the function in part (a) and comment on its behavior near the origin. if x + 0 f(x) : if x = 0
> (a). Expand 1/4√1 + x as a power series. (b). Use part (a) to estimate 1/4√1.1 correct to three decimal places.

