Question: Evaluate the indefinite integral as a power
Evaluate the indefinite integral as a power series. What is the radius of convergence?
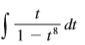
Transcribed Image Text:
dt
> Evaluate the integral. Sx sin'x cos x dx
> Evaluate the integral. 1+ sin x dx SI 1- sin x
> Evaluate the integral. xe* dx /1 + e*
> Evaluate the integral. dx Vx² + 1
> Evaluate the integral. dx х In x — х
> Use a power series to approximate the definite integral to six decimal places. r0.3 Jo 1+ x3 dx
> Evaluate the integral. :+ arcsin. dx VI - x² 1 –
> Evaluate the integral. In(x + 1) ax x?
> Evaluate the integral. e 2x dx 1x 1+ e*
> Evaluate the integral. 1 dx 1+ 2e* — е *
> Evaluate the integral. 1 + x² dx 2
> Evaluate the integral. x? dx хв + 3x3 + 2
> Evaluate the integral. 1 dx /x + 1 + Vx
> Evaluate the integral. m/3_In(tan x) – dx Ja/4 sin x cos x
> Evaluate the integral. sin 2x dx J1+ cos“x
> Evaluate the integral. -dx I + x^^ Vx + 1
> Evaluate the indefinite integral as a power series. What is the radius of convergence? tan x dx
> Evaluate the integral. dx
> Evaluate the integral. de 1 + cos?e
> Evaluate the integral. de 1 + cos 0
> Evaluate the integral. dx J x*/4x? – 1
> Evaluate the integral. dx x* - 16
> Evaluate the integral. x In x dx /x² 1
> Evaluate the integral. fxk + c dx
> Evaluate the integral. dx x^x + x^
> Evaluate the integral. dx x + x/r
> Evaluate the integral. | (x + sin x)² dx
> Evaluate the indefinite integral as a power series. What is the radius of convergence? |x? In(1 + x) dx
> Evaluate the integral. |x' sinh mx dx х* si
> Evaluate the integral. dx Jx(x* + 1)
> Evaluate the integral. 1 x/4x2 + 1
> Evaluate the integral. 1 dx J x?V4x + 1
> Evaluate the integral. 1 dx J x/4x + 1
> Evaluate the integral. x/2 - VI - x² dx
> Evaluate the integral. Sx(x – 1) *dx
> Evaluate the integral. (x – 1)e* dx .2 x
> Evaluate the integral. fx'e "dx
> Evaluate the integral. SVi+e" dx
> Evaluate the indefinite integral as a power series. What is the radius of convergence? i - 1+ t
> Evaluate the integral. dx 1 + x³
> Evaluate the integral. tan'x dx
> Evaluate the integral. |O tan'o do
> Evaluate the integral. | sin 6x cos 3x dx
> Evaluate the integral. sec 0 tan 0 o - J sec'o – sec 0
> Evaluate the integral. /3 sin 0 cot 0 do Jw/6 sec 0
> Evaluate the integral. 1 + sin x dx 1 + cos x
> Evaluate the integral. 12 1 + 4 cot x dx Ja/4 4 - cot x
> Evaluate the integral. |V3 – 2x – x² dx
> Evaluate the integral. 3/3 3 dx 2
> Evaluate the integral. 1 + x dx
> Evaluate the integral. S,le - 1|dx
> Evaluate the integral. S In(x + vx? – T) dx
> Evaluate the integral. S sin Jat dt
> Evaluate the integral. dx J 1+ e*
> Evaluate the integral. 3x² + 1 dx Jo x³ + x? + x +1
> Evaluate the integral. + tan x)? sec x dx
> Evaluate the integral. + dx
> Evaluate the integral. In x -dx x/1 + (In x)²
> Evaluate the integral. | arctan /x dx
> Find a power series representation for f, and graph f and several partial sums sn(x) on the same screen. What happens as n increases? f(x) = tan (2x)
> (a) Approximate f by a Taylor polynomial with degree n at the number a. (b) Use Taylor’s Inequality to estimate the accuracy of the approximation / when x lies in the given interval. (c) Check your result in part (b) by graphing / S
> Evaluate the integral. t cos?t dt Jo CoS
> Evaluate the integral. x? dx VI - x2
> Evaluate the integral. X sec x tan x dx
> Evaluate the integral. In(1 + x²) dx
> Evaluate the integral. ( sin't cos't dt
> Evaluate the integral. 2х — 3 dx x' + 3x
> Evaluate the integral. 1 dx x'/x² – 1
> Evaluate the integral. cos(1/x) · dx ах
> Evaluate the integral. х+ 2 dx 2 х3 + 3х — 4
> Evaluate the integral. Se sin t cos t dt |t sin t
> Find a power series representation for f, and graph f and several partial sums sn(x) on the same screen. What happens as n increases? 1 + x S(x) = In 1- x
> Evaluate the integral. - dx (2х + 1)°
> Evaluate the integral. dt t* + 2
> Evaluate the integral. sin'x dx cos x
> Evaluate the integral. ( Vỹ In y dy
> Evaluate the integral. (3r + 1)7 dx
> Evaluate the integral. cos x dx 1- sin x
> Computer algebra systems sometimes need a helping hand from human beings. Try to evaluate with a computer algebra system. If it doesn’t return an answer, make a substitution that changes the integral into one that the CAS can evaluate.
> Use a computer algebra system to evaluate the integral. Compare the answer with the result of using tables. If the answers are not the same, show that they are equivalent. dx V1 + x
> Use a computer algebra system to evaluate the integral. Compare the answer with the result of using tables. If the answers are not the same, show that they are equivalent. | tan'x dx
> Find a power series representation for f, and graph f and several partial sums sn(x) on the same screen. What happens as n increases? f(x) = In(1 + x*)
> Use a computer algebra system to evaluate the integral. Compare the answer with the result of using tables. If the answers are not the same, show that they are equivalent. - x² dx
> Use a computer algebra system to evaluate the integral. Compare the answer with the result of using tables. If the answers are not the same, show that they are equivalent. | cos*x dx
> Use a computer algebra system to evaluate the integral. Compare the answer with the result of using tables. If the answers are not the same, show that they are equivalent. dx e*(3e* + 2)
> Use a computer algebra system to evaluate the integral. Compare the answer with the result of using tables. If the answers are not the same, show that they are equivalent. fxVF + 4 dx
> Use a computer algebra system to evaluate the integral. Compare the answer with the result of using tables. If the answers are not the same, show that they are equivalent. Sese'x dx
> Use a computer algebra system to evaluate the integral. Compare the answer with the result of using tables. If the answers are not the same, show that they are equivalent. | sec'x dx
> Verify Formula 53 in the Table of Integrals (a) by differentiation and (b) by using the substitution t = a + bu.
> Find the volume of the solid obtained when the region under the curve y = arcsin x, x > 0, is rotated about the y-axis.
> Find a power series representation for f, and graph f and several partial sums sn(x) on the same screen. What happens as n increases? 2 S(x) – %3D x? + 1
> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. sec20 tan´0 do 9 – tan?0
> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. x*dx r10 – 2 - 2
> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. |e' sin(at – 3) dt
> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. 2x – 1 dx
> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. dx 2x
> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. cos '(x-2)
> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. x*e* dx
> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. 4 + (In x)² – dx
> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. Sx'arcsin(x²) dx

