Question: Use a computer algebra system to evaluate
Use a computer algebra system to evaluate the integral. Compare the answer with the result of using tables. If the answers are not the same, show that they are equivalent.
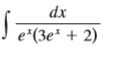
Transcribed Image Text:
dx e*(3e* + 2)
> Evaluate the integral. fx'e "dx
> Evaluate the integral. SVi+e" dx
> Evaluate the indefinite integral as a power series. What is the radius of convergence? i - 1+ t
> Evaluate the integral. dx 1 + x³
> Evaluate the integral. tan'x dx
> Evaluate the integral. |O tan'o do
> Evaluate the integral. | sin 6x cos 3x dx
> Evaluate the integral. sec 0 tan 0 o - J sec'o – sec 0
> Evaluate the integral. /3 sin 0 cot 0 do Jw/6 sec 0
> Evaluate the integral. 1 + sin x dx 1 + cos x
> Evaluate the integral. 12 1 + 4 cot x dx Ja/4 4 - cot x
> Evaluate the integral. |V3 – 2x – x² dx
> Evaluate the integral. 3/3 3 dx 2
> Evaluate the indefinite integral as a power series. What is the radius of convergence? dt
> Evaluate the integral. 1 + x dx
> Evaluate the integral. S,le - 1|dx
> Evaluate the integral. S In(x + vx? – T) dx
> Evaluate the integral. S sin Jat dt
> Evaluate the integral. dx J 1+ e*
> Evaluate the integral. 3x² + 1 dx Jo x³ + x? + x +1
> Evaluate the integral. + tan x)? sec x dx
> Evaluate the integral. + dx
> Evaluate the integral. In x -dx x/1 + (In x)²
> Evaluate the integral. | arctan /x dx
> Find a power series representation for f, and graph f and several partial sums sn(x) on the same screen. What happens as n increases? f(x) = tan (2x)
> (a) Approximate f by a Taylor polynomial with degree n at the number a. (b) Use Taylor’s Inequality to estimate the accuracy of the approximation / when x lies in the given interval. (c) Check your result in part (b) by graphing / S
> Evaluate the integral. t cos?t dt Jo CoS
> Evaluate the integral. x? dx VI - x2
> Evaluate the integral. X sec x tan x dx
> Evaluate the integral. In(1 + x²) dx
> Evaluate the integral. ( sin't cos't dt
> Evaluate the integral. 2х — 3 dx x' + 3x
> Evaluate the integral. 1 dx x'/x² – 1
> Evaluate the integral. cos(1/x) · dx ах
> Evaluate the integral. х+ 2 dx 2 х3 + 3х — 4
> Evaluate the integral. Se sin t cos t dt |t sin t
> Find a power series representation for f, and graph f and several partial sums sn(x) on the same screen. What happens as n increases? 1 + x S(x) = In 1- x
> Evaluate the integral. - dx (2х + 1)°
> Evaluate the integral. dt t* + 2
> Evaluate the integral. sin'x dx cos x
> Evaluate the integral. ( Vỹ In y dy
> Evaluate the integral. (3r + 1)7 dx
> Evaluate the integral. cos x dx 1- sin x
> Computer algebra systems sometimes need a helping hand from human beings. Try to evaluate with a computer algebra system. If it doesn’t return an answer, make a substitution that changes the integral into one that the CAS can evaluate.
> Use a computer algebra system to evaluate the integral. Compare the answer with the result of using tables. If the answers are not the same, show that they are equivalent. dx V1 + x
> Use a computer algebra system to evaluate the integral. Compare the answer with the result of using tables. If the answers are not the same, show that they are equivalent. | tan'x dx
> Find a power series representation for f, and graph f and several partial sums sn(x) on the same screen. What happens as n increases? f(x) = In(1 + x*)
> Use a computer algebra system to evaluate the integral. Compare the answer with the result of using tables. If the answers are not the same, show that they are equivalent. - x² dx
> Use a computer algebra system to evaluate the integral. Compare the answer with the result of using tables. If the answers are not the same, show that they are equivalent. | cos*x dx
> Use a computer algebra system to evaluate the integral. Compare the answer with the result of using tables. If the answers are not the same, show that they are equivalent. fxVF + 4 dx
> Use a computer algebra system to evaluate the integral. Compare the answer with the result of using tables. If the answers are not the same, show that they are equivalent. Sese'x dx
> Use a computer algebra system to evaluate the integral. Compare the answer with the result of using tables. If the answers are not the same, show that they are equivalent. | sec'x dx
> Verify Formula 53 in the Table of Integrals (a) by differentiation and (b) by using the substitution t = a + bu.
> Find the volume of the solid obtained when the region under the curve y = arcsin x, x > 0, is rotated about the y-axis.
> Find a power series representation for f, and graph f and several partial sums sn(x) on the same screen. What happens as n increases? 2 S(x) – %3D x? + 1
> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. sec20 tan´0 do 9 – tan?0
> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. x*dx r10 – 2 - 2
> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. |e' sin(at – 3) dt
> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. 2x – 1 dx
> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. dx 2x
> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. cos '(x-2)
> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. x*e* dx
> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. 4 + (In x)² – dx
> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. Sx'arcsin(x²) dx
> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. ( sec'x dx
> Find a power series representation for the function and determine the radius of convergence. x² + x f(x)- (1 – x)'
> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. x'/4x² – xª dx Jo
> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. · dx 3 - e2x
> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. sin 20 do /5 – sin 0
> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. S sin'x cos x In(sin x) dx
> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. dx 2x – 3x?
> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. S V6 + 4y – 4y² dy
> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. dt 21
> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. coth(1/y) dy y?
> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. x'sinx dx
> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. arctan Vr dx
> Find a power series representation for the function and determine the radius of convergence. 1 + x (1 – x)? S(x -
> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. fx/2 + x* dx
> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. ( cos"0 do
> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. /2y² – 3 dy ,2
> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. 9x² x? /9х2 + 4 dx
> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. w/8 arctan 2x dx
> Use the indicated entry in the Table of Integrals on the Reference Pages to evaluate the integral. tan(Tx/6) dx; entry 69
> Use the indicated entry in the Table of Integrals on the Reference Pages to evaluate the integral. I V - x dx; entry 113
> Use the indicated entry in the Table of Integrals on the Reference Pages to evaluate the integral. w/2 cos 5x cos 2x dx; entry 80
> Show that 1 3 Tn + 2 3 Mn = S2n
> Show that 1 2 (Tn + Mn) = T2n
> Find a power series representation for the function and determine the radius of convergence. 3 f(x) = 2 - x
> Sketch the graph of a continuous function on [0, 2] for which the right endpoint approximation with n = 2 is more accurate than Simpson’s Rule.
> Sketch the graph of a continuous function on [0, 2] for which the Trapezoidal Rule with n = 2 is more accurate than the Midpoint Rule.
> The region bounded by the curve y = 1/(1+e-x) the x- and y-axes, and the line x = 10 is rotated about the x-axis. Use Simpson’s Rule with n = 10 to estimate the volume of the resulting solid.
> The table shows values of a force function f(x), where x is measured in meters and f(x) in newtons. Use Simpson’s Rule to estimate the work done by the force in moving an object a distance of 18 m. 6 9 3 12 15 18 f(x) 9.8 9.1 8.5 8
> Use Simpson’s Rule with n = 8 to estimate the volume of the solid obtained by rotating the region shown in the figure about (a) the x-axis and (b) the y-axis. y. 4 8 10 x 4. 2. 2.
> Shown is the graph of traffic on an Internet service provider’s T1 data line from midnight to 8:00 am. D is the data throughput, measured in megabits per second. Use Simpson’s Rule to estimate the total amount of data
> Find a power series representation for the function and determine the radius of convergence. S(x) · (1 + 4x)?
> The table (supplied by San Diego Gas and Electric) gives the power consumption P in megawatts in San Diego County from midnight to 6:00 am on a day in December. Use Simpson’s Rule to estimate the energy used during that time period. (Us
> Water leaked from a tank at a rate of r(t) liters per hour, where the graph of r is as shown. Use Simpson’s Rule to estimate the total amount of water that leaked out during the first 6 hours. 4 2 0 2 4 6 1 (seconds)
> The graph of the acceleration a(t) of a car measured in ft/s2 is shown. Use Simpson’s Rule to estimate the increase in the velocity of the car during the 6-second time interval. 12 8 4 4 6 t(seconds) 2.
> A radar gun was used to record the speed of a runner during the first 5 seconds of a race (see the table). Use Simpson’s Rule to estimate the distance the runner covered during those 5 seconds. t (s) v (m/s) 1 (s) v (m/
> A graph of the temperature in Boston on August 11, 2013, is shown. Use Simpson’s Rule with n = 12 to estimate the average temperature on that day. TA (F) 80 70 60- noon 4 8 4.

