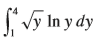Question: Evaluate the integral. /

> Evaluate the indefinite integral as a power series. What is the radius of convergence? |x? In(1 + x) dx

> Evaluate the integral. |x' sinh mx dx х* si

> Evaluate the integral. dx Jx(x* + 1)

> Evaluate the integral. 1 x/4x2 + 1

> Evaluate the integral. 1 dx J x?V4x + 1

> Evaluate the integral. 1 dx J x/4x + 1

> Evaluate the integral. x/2 - VI - x² dx

> Evaluate the integral. Sx(x – 1) *dx

> Evaluate the integral. (x – 1)e* dx .2 x

> Evaluate the integral. fx'e "dx

> Evaluate the integral. SVi+e" dx

> Evaluate the indefinite integral as a power series. What is the radius of convergence? i - 1+ t

> Evaluate the integral. dx 1 + x³

> Evaluate the integral. tan'x dx

> Evaluate the integral. |O tan'o do

> Evaluate the integral. | sin 6x cos 3x dx

> Evaluate the integral. sec 0 tan 0 o - J sec'o – sec 0

> Evaluate the integral. /3 sin 0 cot 0 do Jw/6 sec 0

> Evaluate the integral. 1 + sin x dx 1 + cos x

> Evaluate the integral. 12 1 + 4 cot x dx Ja/4 4 - cot x

> Evaluate the integral. |V3 – 2x – x² dx

> Evaluate the integral. 3/3 3 dx 2

> Evaluate the indefinite integral as a power series. What is the radius of convergence? dt

> Evaluate the integral. 1 + x dx

> Evaluate the integral. S,le - 1|dx

> Evaluate the integral. S In(x + vx? – T) dx

> Evaluate the integral. S sin Jat dt

> Evaluate the integral. dx J 1+ e*

> Evaluate the integral. 3x² + 1 dx Jo x³ + x? + x +1

> Evaluate the integral. + tan x)? sec x dx

> Evaluate the integral. + dx

> Evaluate the integral. In x -dx x/1 + (In x)²

> Evaluate the integral. | arctan /x dx

> Find a power series representation for f, and graph f and several partial sums sn(x) on the same screen. What happens as n increases? f(x) = tan (2x)

> (a) Approximate f by a Taylor polynomial with degree n at the number a. (b) Use Taylor’s Inequality to estimate the accuracy of the approximation / when x lies in the given interval. (c) Check your result in part (b) by graphing / S

> Evaluate the integral. t cos?t dt Jo CoS

> Evaluate the integral. x? dx VI - x2

> Evaluate the integral. X sec x tan x dx

> Evaluate the integral. In(1 + x²) dx

> Evaluate the integral. ( sin't cos't dt

> Evaluate the integral. 2х — 3 dx x' + 3x

> Evaluate the integral. 1 dx x'/x² – 1

> Evaluate the integral. cos(1/x) · dx ах

> Evaluate the integral. х+ 2 dx 2 х3 + 3х — 4

> Evaluate the integral. Se sin t cos t dt |t sin t

> Find a power series representation for f, and graph f and several partial sums sn(x) on the same screen. What happens as n increases? 1 + x S(x) = In 1- x

> Evaluate the integral. - dx (2х + 1)°

> Evaluate the integral. dt t* + 2

> Evaluate the integral. sin'x dx cos x

> Evaluate the integral. (3r + 1)7 dx

> Evaluate the integral. cos x dx 1- sin x

> Computer algebra systems sometimes need a helping hand from human beings. Try to evaluate with a computer algebra system. If it doesn’t return an answer, make a substitution that changes the integral into one that the CAS can evaluate.

> Use a computer algebra system to evaluate the integral. Compare the answer with the result of using tables. If the answers are not the same, show that they are equivalent. dx V1 + x

> Use a computer algebra system to evaluate the integral. Compare the answer with the result of using tables. If the answers are not the same, show that they are equivalent. | tan'x dx

> Find a power series representation for f, and graph f and several partial sums sn(x) on the same screen. What happens as n increases? f(x) = In(1 + x*)

> Use a computer algebra system to evaluate the integral. Compare the answer with the result of using tables. If the answers are not the same, show that they are equivalent. - x² dx

> Use a computer algebra system to evaluate the integral. Compare the answer with the result of using tables. If the answers are not the same, show that they are equivalent. | cos*x dx

> Use a computer algebra system to evaluate the integral. Compare the answer with the result of using tables. If the answers are not the same, show that they are equivalent. dx e*(3e* + 2)

> Use a computer algebra system to evaluate the integral. Compare the answer with the result of using tables. If the answers are not the same, show that they are equivalent. fxVF + 4 dx

> Use a computer algebra system to evaluate the integral. Compare the answer with the result of using tables. If the answers are not the same, show that they are equivalent. Sese'x dx

> Use a computer algebra system to evaluate the integral. Compare the answer with the result of using tables. If the answers are not the same, show that they are equivalent. | sec'x dx

> Verify Formula 53 in the Table of Integrals (a) by differentiation and (b) by using the substitution t = a + bu.

> Find the volume of the solid obtained when the region under the curve y = arcsin x, x > 0, is rotated about the y-axis.

> Find a power series representation for f, and graph f and several partial sums sn(x) on the same screen. What happens as n increases? 2 S(x) – %3D x? + 1

> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. sec20 tan´0 do 9 – tan?0

> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. x*dx r10 – 2 - 2

> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. |e' sin(at – 3) dt

> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. 2x – 1 dx

> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. dx 2x

> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. cos '(x-2)

> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. x*e* dx

> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. 4 + (In x)² – dx

> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. Sx'arcsin(x²) dx

> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. ( sec'x dx

> Find a power series representation for the function and determine the radius of convergence. x² + x f(x)- (1 – x)'

> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. x'/4x² – xª dx Jo

> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. · dx 3 - e2x

> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. sin 20 do /5 – sin 0

> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. S sin'x cos x In(sin x) dx

> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. dx 2x – 3x?

> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. S V6 + 4y – 4y² dy

> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. dt 21

> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. coth(1/y) dy y?

> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. x'sinx dx

> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. arctan Vr dx

> Find a power series representation for the function and determine the radius of convergence. 1 + x (1 – x)? S(x -

> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. fx/2 + x* dx

> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. ( cos"0 do

> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. /2y² – 3 dy ,2

> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. 9x² x? /9х2 + 4 dx

> Use the Table of Integrals on Reference Pages 6–10 to evaluate the integral. w/8 arctan 2x dx

> Use the indicated entry in the Table of Integrals on the Reference Pages to evaluate the integral. tan(Tx/6) dx; entry 69

> Use the indicated entry in the Table of Integrals on the Reference Pages to evaluate the integral. I V - x dx; entry 113

> Use the indicated entry in the Table of Integrals on the Reference Pages to evaluate the integral. w/2 cos 5x cos 2x dx; entry 80

> Show that 1 3 Tn + 2 3 Mn = S2n

> Show that 1 2 (Tn + Mn) = T2n

> Find a power series representation for the function and determine the radius of convergence. 3 f(x) = 2 - x

> Sketch the graph of a continuous function on [0, 2] for which the right endpoint approximation with n = 2 is more accurate than Simpson’s Rule.

> Sketch the graph of a continuous function on [0, 2] for which the Trapezoidal Rule with n = 2 is more accurate than the Midpoint Rule.

> The region bounded by the curve y = 1/(1+e-x) the x- and y-axes, and the line x = 10 is rotated about the x-axis. Use Simpson’s Rule with n = 10 to estimate the volume of the resulting solid.